Stochastic gradient descent methods for estimation with large data sets
Paper and Code
Sep 22, 2015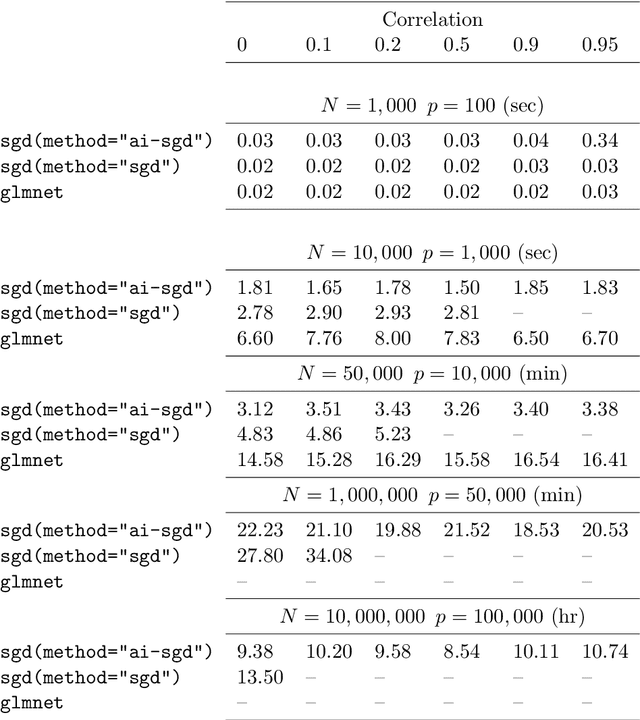
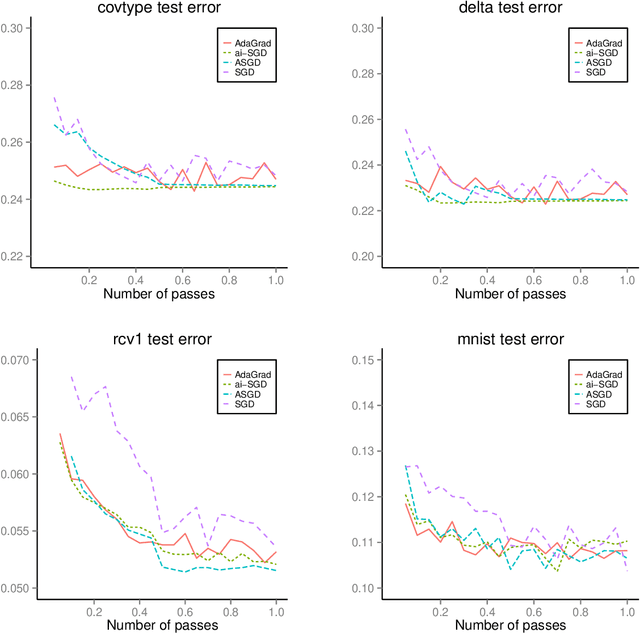
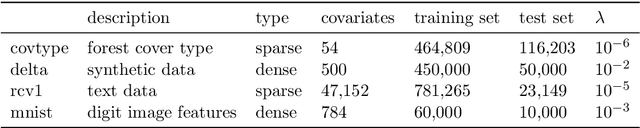
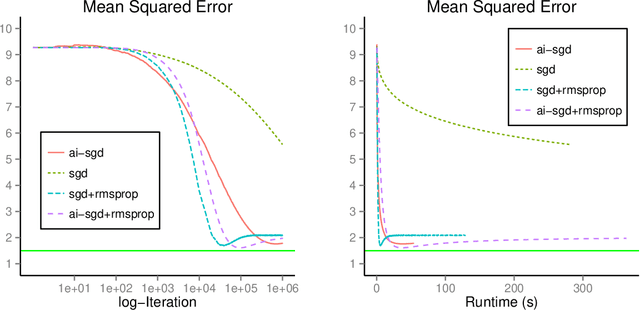
We develop methods for parameter estimation in settings with large-scale data sets, where traditional methods are no longer tenable. Our methods rely on stochastic approximations, which are computationally efficient as they maintain one iterate as a parameter estimate, and successively update that iterate based on a single data point. When the update is based on a noisy gradient, the stochastic approximation is known as standard stochastic gradient descent, which has been fundamental in modern applications with large data sets. Additionally, our methods are numerically stable because they employ implicit updates of the iterates. Intuitively, an implicit update is a shrinked version of a standard one, where the shrinkage factor depends on the observed Fisher information at the corresponding data point. This shrinkage prevents numerical divergence of the iterates, which can be caused either by excess noise or outliers. Our sgd package in R offers the most extensive and robust implementation of stochastic gradient descent methods. We demonstrate that sgd dominates alternative software in runtime for several estimation problems with massive data sets. Our applications include the wide class of generalized linear models as well as M-estimation for robust regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge