Stable Robbins-Monro approximations through stochastic proximal updates
Paper and Code
Mar 05, 2018
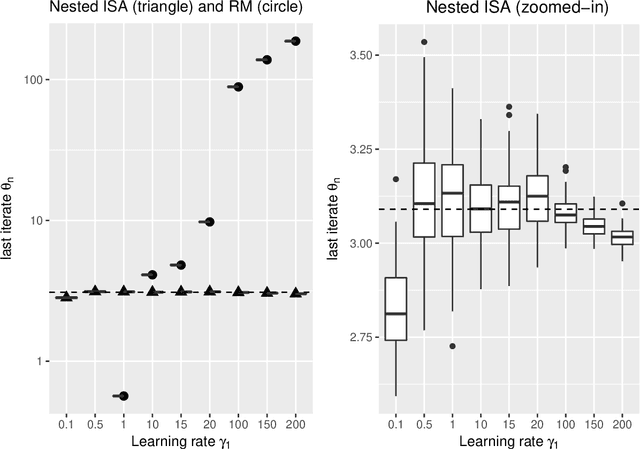
The need for parameter estimation with massive data has reinvigorated interest in iterative estimation procedures. Stochastic approximations, such as stochastic gradient descent, are at the forefront of this recent development because they yield simple, generic, and extremely fast iterative estimation procedures. Such stochastic approximations, however, are often numerically unstable. As a consequence, current practice has turned to proximal operators, which can induce stable parameter updates within iterations. While the majority of classical iterative estimation procedures are subsumed by the framework of Robbins and Monro (1951), there is no such generalization for stochastic approximations with proximal updates. In this paper, we conceptualize a general stochastic approximation method with proximal updates. This method can be applied even in situations where the analytical form of the objective is not known, and so it generalizes many stochastic gradient procedures with proximal operators currently in use. Our theoretical analysis indicates that the proposed method has important stability benefits over the classical stochastic approximation method. Exact instantiations of the proposed method are challenging, but we show that approximate instantiations lead to procedures that are easy to implement, and still dominate classical procedures by achieving numerical stability without tradeoffs. This last advantage is akin to that seen in deterministic proximal optimization, where the framework is typically impossible to instantiate exactly, but where approximate instantiations lead to new optimization procedures that dominate classical ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge