Cooperative Multi-agent RL with Communication Constraints

Cooperative MARL often assumes frequent access to global information in a data buffer, such as team rewards or other agents' actions, which is typically unrealistic in decentralized MARL systems due to high communication costs. When communication is limited, agents must rely on outdated information to estimate gradients and update their policies. A common approach to handle missing data is called importance sampling, in which we reweigh old data from a base policy to estimate gradients for the current policy. However, it quickly becomes unstable when the communication is limited (i.e. missing data probability is high), so that the base policy in importance sampling is outdated. To address this issue, we propose a technique called base policy prediction, which utilizes old gradients to predict the policy update and collect samples for a sequence of base policies, which reduces the gap between the base policy and the current policy. This approach enables effective learning with significantly fewer communication rounds, since the samples of predicted base policies could be collected within one communication round. Theoretically, we show that our algorithm converges to an $\varepsilon$-Nash equilibrium in potential games with only $O(\varepsilon^{-3/4})$ communication rounds and $O(poly(\max_i |A_i|)\varepsilon^{-11/4})$ samples, improving existing state-of-the-art results in communication cost, as well as sample complexity without the exponential dependence on the joint action space size. We also extend these results to general Markov Cooperative Games to find an agent-wise local maximum. Empirically, we test the base policy prediction algorithm in both simulated games and MAPPO for complex environments.

Token-Level LLM Collaboration via FusionRoute

Large language models (LLMs) exhibit strengths across diverse domains. However, achieving strong performance across these domains with a single general-purpose model typically requires scaling to sizes that are prohibitively expensive to train and deploy. On the other hand, while smaller domain-specialized models are much more efficient, they struggle to generalize beyond their training distributions. To address this dilemma, we propose FusionRoute, a robust and effective token-level multi-LLM collaboration framework in which a lightweight router simultaneously (i) selects the most suitable expert at each decoding step and (ii) contributes a complementary logit that refines or corrects the selected expert's next-token distribution via logit addition. Unlike existing token-level collaboration methods that rely solely on fixed expert outputs, we provide a theoretical analysis showing that pure expert-only routing is fundamentally limited: unless strong global coverage assumptions hold, it cannot in general realize the optimal decoding policy. By augmenting expert selection with a trainable complementary generator, FusionRoute expands the effective policy class and enables recovery of optimal value functions under mild conditions. Empirically, across both Llama-3 and Gemma-2 families and diverse benchmarks spanning mathematical reasoning, code generation, and instruction following, FusionRoute outperforms both sequence- and token-level collaboration, model merging, and direct fine-tuning, while remaining competitive with domain experts on their respective tasks.

Projection Optimization: A General Framework for Multi-Objective and Multi-Group RLHF

Reinforcement Learning with Human Feedback (RLHF) is a widely used fine-tuning approach that aligns machine learning model, particularly Language Model (LM) with human preferences. There are typically multiple objectives driving the preference, hence humans find it easier to express per-objective comparisons rather than a global preference between two choices. Multi-Objective RLHF (MORLHF) aims to use per-objective preference feedback and achieve Pareto optimality among these objectives by aggregating them into a single unified objective for optimization. However, nearly all prior works rely on linear aggregation, which rules out policies that favor specific objectives such as the worst one. The only existing approach using non-linear aggregation is computationally expensive due to its reward-based nature and the need for retraining whenever the aggregation parameters change. In this work, we address this limitation by transforming the non-linear aggregation maximization problem into a series of sub-problems. Each sub-problem involves only linear aggregation, making it computationally efficient to solve. We further extend our framework to handle multi-group scenarios, where each group has distinct weights for the objectives. Our method enables achieving consensus or maximizing the aggregated objective across all groups. Theoretically, we demonstrate that our algorithmic framework achieves sublinear regret and can be easily adapted to a reward-free algorithm. Empirically, leveraging our theoretical insights, we propose a nearly training-free algorithm once the optimal policies for individual objectives are obtained.

A Correction of Pseudo Log-Likelihood Method

Pseudo log-likelihood is a type of maximum likelihood estimation (MLE) method used in various fields including contextual bandits, influence maximization of social networks, and causal bandits. However, in previous literature \citep{li2017provably, zhang2022online, xiong2022combinatorial, feng2023combinatorial1, feng2023combinatorial2}, the log-likelihood function may not be bounded, which may result in the algorithm they proposed not well-defined. In this paper, we give a counterexample that the maximum pseudo log-likelihood estimation fails and then provide a solution to correct the algorithms in \citep{li2017provably, zhang2022online, xiong2022combinatorial, feng2023combinatorial1, feng2023combinatorial2}.

Sample-Efficient Multi-Agent RL: An Optimization Perspective

We study multi-agent reinforcement learning (MARL) for the general-sum Markov Games (MGs) under the general function approximation. In order to find the minimum assumption for sample-efficient learning, we introduce a novel complexity measure called the Multi-Agent Decoupling Coefficient (MADC) for general-sum MGs. Using this measure, we propose the first unified algorithmic framework that ensures sample efficiency in learning Nash Equilibrium, Coarse Correlated Equilibrium, and Correlated Equilibrium for both model-based and model-free MARL problems with low MADC. We also show that our algorithm provides comparable sublinear regret to the existing works. Moreover, our algorithm combines an equilibrium-solving oracle with a single objective optimization subprocedure that solves for the regularized payoff of each deterministic joint policy, which avoids solving constrained optimization problems within data-dependent constraints (Jin et al. 2020; Wang et al. 2023) or executing sampling procedures with complex multi-objective optimization problems (Foster et al. 2023), thus being more amenable to empirical implementation.

How Over-Parameterization Slows Down Gradient Descent in Matrix Sensing: The Curses of Symmetry and Initialization

This paper rigorously shows how over-parameterization changes the convergence behaviors of gradient descent (GD) for the matrix sensing problem, where the goal is to recover an unknown low-rank ground-truth matrix from near-isotropic linear measurements. First, we consider the symmetric setting with the symmetric parameterization where $M^* \in \mathbb{R}^{n \times n}$ is a positive semi-definite unknown matrix of rank $r \ll n$, and one uses a symmetric parameterization $XX^\top$ to learn $M^*$. Here $X \in \mathbb{R}^{n \times k}$ with $k > r$ is the factor matrix. We give a novel $\Omega (1/T^2)$ lower bound of randomly initialized GD for the over-parameterized case ($k >r$) where $T$ is the number of iterations. This is in stark contrast to the exact-parameterization scenario ($k=r$) where the convergence rate is $\exp (-\Omega (T))$. Next, we study asymmetric setting where $M^* \in \mathbb{R}^{n_1 \times n_2}$ is the unknown matrix of rank $r \ll \min\{n_1,n_2\}$, and one uses an asymmetric parameterization $FG^\top$ to learn $M^*$ where $F \in \mathbb{R}^{n_1 \times k}$ and $G \in \mathbb{R}^{n_2 \times k}$. Building on prior work, we give a global exact convergence result of randomly initialized GD for the exact-parameterization case ($k=r$) with an $\exp (-\Omega(T))$ rate. Furthermore, we give the first global exact convergence result for the over-parameterization case ($k>r$) with an $\exp(-\Omega(\alpha^2 T))$ rate where $\alpha$ is the initialization scale. This linear convergence result in the over-parameterization case is especially significant because one can apply the asymmetric parameterization to the symmetric setting to speed up from $\Omega (1/T^2)$ to linear convergence. On the other hand, we propose a novel method that only modifies one step of GD and obtains a convergence rate independent of $\alpha$, recovering the rate in the exact-parameterization case.

A General Framework for Sequential Decision-Making under Adaptivity Constraints

We take the first step in studying general sequential decision-making under two adaptivity constraints: rare policy switch and batch learning. First, we provide a general class called the Eluder Condition class, which includes a wide range of reinforcement learning classes. Then, for the rare policy switch constraint, we provide a generic algorithm to achieve a $\widetilde{\mathcal{O}}(\log K) $ switching cost with a $\widetilde{\mathcal{O}}(\sqrt{K})$ regret on the EC class. For the batch learning constraint, we provide an algorithm that provides a $\widetilde{\mathcal{O}}(\sqrt{K}+K/B)$ regret with the number of batches $B.$ This paper is the first work considering rare policy switch and batch learning under general function classes, which covers nearly all the models studied in the previous works such as tabular MDP (Bai et al. 2019; Zhang et al. 2020), linear MDP (Wang et al. 2021; Gao et al. 2021), low eluder dimension MDP (Kong et al. 2021; Gao et al. 2021), generalized linear function approximation (Qiao et al. 2023), and also some new classes such as the low $D_\Delta$-type Bellman eluder dimension problem, linear mixture MDP, kernelized nonlinear regulator and undercomplete partially observed Markov decision process (POMDP).

Provably Safe Reinforcement Learning with Step-wise Violation Constraints

In this paper, we investigate a novel safe reinforcement learning problem with step-wise violation constraints. Our problem differs from existing works in that we consider stricter step-wise violation constraints and do not assume the existence of safe actions, making our formulation more suitable for safety-critical applications which need to ensure safety in all decision steps and may not always possess safe actions, e.g., robot control and autonomous driving. We propose a novel algorithm SUCBVI, which guarantees $\widetilde{O}(\sqrt{ST})$ step-wise violation and $\widetilde{O}(\sqrt{H^3SAT})$ regret. Lower bounds are provided to validate the optimality in both violation and regret performance with respect to $S$ and $T$. Moreover, we further study a novel safe reward-free exploration problem with step-wise violation constraints. For this problem, we design an $(\varepsilon,\delta)$-PAC algorithm SRF-UCRL, which achieves nearly state-of-the-art sample complexity $\widetilde{O}((\frac{S^2AH^2}{\varepsilon}+\frac{H^4SA}{\varepsilon^2})(\log(\frac{1}{\delta})+S))$, and guarantees $\widetilde{O}(\sqrt{ST})$ violation during the exploration. The experimental results demonstrate the superiority of our algorithms in safety performance, and corroborate our theoretical results.

Combinatorial Causal Bandits without Graph Skeleton

In combinatorial causal bandits (CCB), the learning agent chooses a subset of variables in each round to intervene and collects feedback from the observed variables to minimize expected regret or sample complexity. Previous works study this problem in both general causal models and binary generalized linear models (BGLMs). However, all of them require prior knowledge of causal graph structure. This paper studies the CCB problem without the graph structure on binary general causal models and BGLMs. We first provide an exponential lower bound of cumulative regrets for the CCB problem on general causal models. To overcome the exponentially large space of parameters, we then consider the CCB problem on BGLMs. We design a regret minimization algorithm for BGLMs even without the graph skeleton and show that it still achieves $O(\sqrt{T}\ln T)$ expected regret. This asymptotic regret is the same as the state-of-art algorithms relying on the graph structure. Moreover, we sacrifice the regret to $O(T^{\frac{2}{3}}\ln T)$ to remove the weight gap covered by the asymptotic notation. At last, we give some discussions and algorithms for pure exploration of the CCB problem without the graph structure.

Pure Exploration of Causal Bandits

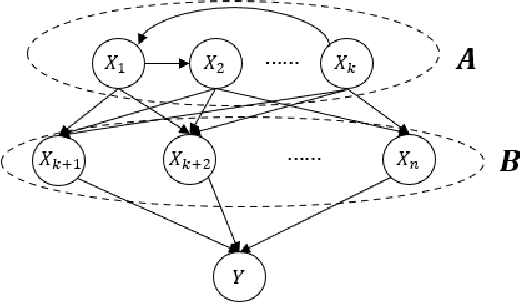
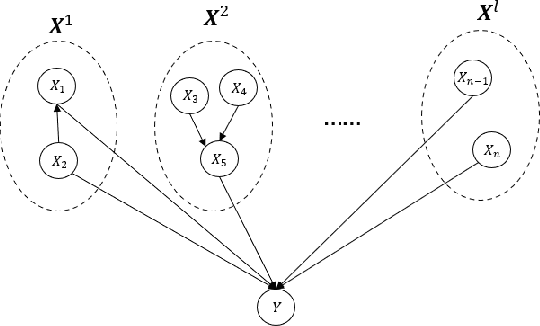
Causal bandit problem integrates causal inference with multi-armed bandits. The pure exploration of causal bandits is the following online learning task: given a causal graph with unknown causal inference distributions, in each round we can choose to either intervene one variable or do no intervention, and observe the random outcomes of all random variables, with the goal that using as few rounds as possible, we can output an intervention that gives the best (or almost best) expected outcome on the reward variable $Y$ with probability at least $1-\delta$, where $\delta$ is a given confidence level. We provide first gap-dependent fully adaptive pure exploration algorithms on three types of causal models including parallel graphs, general graphs with small number of backdoor parents, and binary generalized linear models. Our algorithms improve both prior causal bandit algorithms, which are not adaptive to reward gaps, and prior adaptive pure exploration algorithms, which do not utilize the special features of causal bandits.