Pure Exploration of Causal Bandits
Paper and Code
Jun 16, 2022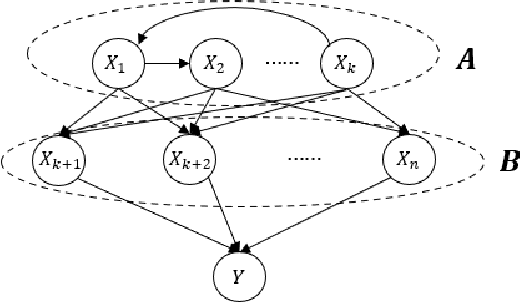
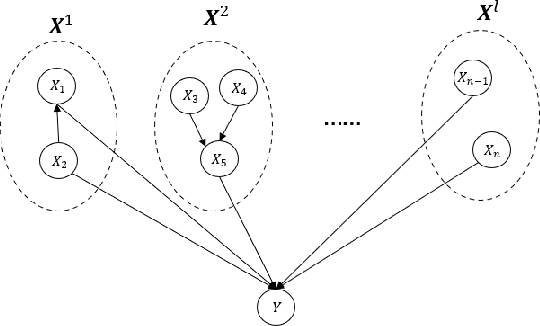
Causal bandit problem integrates causal inference with multi-armed bandits. The pure exploration of causal bandits is the following online learning task: given a causal graph with unknown causal inference distributions, in each round we can choose to either intervene one variable or do no intervention, and observe the random outcomes of all random variables, with the goal that using as few rounds as possible, we can output an intervention that gives the best (or almost best) expected outcome on the reward variable $Y$ with probability at least $1-\delta$, where $\delta$ is a given confidence level. We provide first gap-dependent fully adaptive pure exploration algorithms on three types of causal models including parallel graphs, general graphs with small number of backdoor parents, and binary generalized linear models. Our algorithms improve both prior causal bandit algorithms, which are not adaptive to reward gaps, and prior adaptive pure exploration algorithms, which do not utilize the special features of causal bandits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge