Provably Convergent Policy Optimization via Metric-aware Trust Region Methods

Trust-region methods based on Kullback-Leibler divergence are pervasively used to stabilize policy optimization in reinforcement learning. In this paper, we exploit more flexible metrics and examine two natural extensions of policy optimization with Wasserstein and Sinkhorn trust regions, namely Wasserstein policy optimization (WPO) and Sinkhorn policy optimization (SPO). Instead of restricting the policy to a parametric distribution class, we directly optimize the policy distribution and derive their closed-form policy updates based on the Lagrangian duality. Theoretically, we show that WPO guarantees a monotonic performance improvement, and SPO provably converges to WPO as the entropic regularizer diminishes. Moreover, we prove that with a decaying Lagrangian multiplier to the trust region constraint, both methods converge to global optimality. Experiments across tabular domains, robotic locomotion, and continuous control tasks further demonstrate the performance improvement of both approaches, more robustness of WPO to sample insufficiency, and faster convergence of SPO, over state-of-art policy gradient methods.

Towards Optimal Pricing of Demand Response -- A Nonparametric Constrained Policy Optimization Approach

Demand response (DR) has been demonstrated to be an effective method for reducing peak load and mitigating uncertainties on both the supply and demand sides of the electricity market. One critical question for DR research is how to appropriately adjust electricity prices in order to shift electrical load from peak to off-peak hours. In recent years, reinforcement learning (RL) has been used to address the price-based DR problem because it is a model-free technique that does not necessitate the identification of models for end-use customers. However, the majority of RL methods cannot guarantee the stability and optimality of the learned pricing policy, which is undesirable in safety-critical power systems and may result in high customer bills. In this paper, we propose an innovative nonparametric constrained policy optimization approach that improves optimality while ensuring stability of the policy update, by removing the restrictive assumption on policy representation that the majority of the RL literature adopts: the policy must be parameterized or fall into a certain distribution class. We derive a closed-form expression of optimal policy update for each iteration and develop an efficient on-policy actor-critic algorithm to address the proposed constrained policy optimization problem. The experiments on two DR cases show the superior performance of our proposed nonparametric constrained policy optimization method compared with state-of-the-art RL algorithms.

Decision-Dependent Distributionally Robust Markov Decision Process Method in Dynamic Epidemic Control

In this paper, we present a Distributionally Robust Markov Decision Process (DRMDP) approach for addressing the dynamic epidemic control problem. The Susceptible-Exposed-Infectious-Recovered (SEIR) model is widely used to represent the stochastic spread of infectious diseases, such as COVID-19. While Markov Decision Processes (MDP) offers a mathematical framework for identifying optimal actions, such as vaccination and transmission-reducing intervention, to combat disease spreading according to the SEIR model. However, uncertainties in these scenarios demand a more robust approach that is less reliant on error-prone assumptions. The primary objective of our study is to introduce a new DRMDP framework that allows for an ambiguous distribution of transition dynamics. Specifically, we consider the worst-case distribution of these transition probabilities within a decision-dependent ambiguity set. To overcome the computational complexities associated with policy determination, we propose an efficient Real-Time Dynamic Programming (RTDP) algorithm that is capable of computing optimal policies based on the reformulated DRMDP model in an accurate, timely, and scalable manner. Comparative analysis against the classic MDP model demonstrates that the DRMDP achieves a lower proportion of infections and susceptibilities at a reduced cost.

Model-Informed Generative Adversarial Network (MI-GAN) for Learning Optimal Power Flow

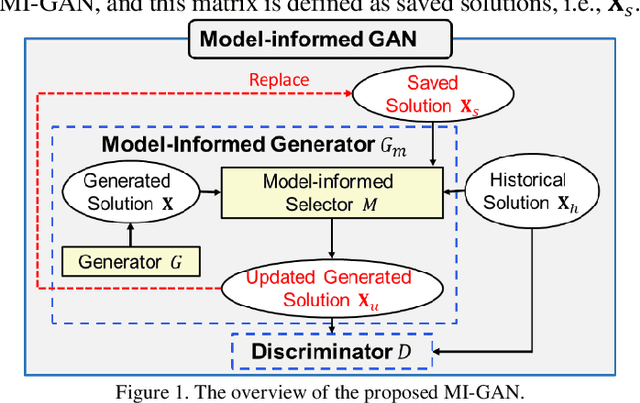
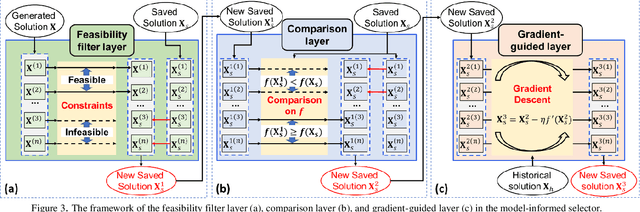
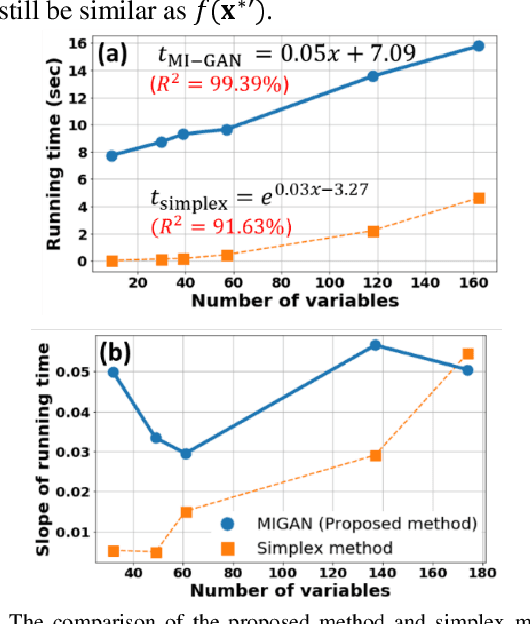
The optimal power flow (OPF) problem, as a critical component of power system operations, becomes increasingly difficult to solve due to the variability, intermittency, and unpredictability of renewable energy brought to the power system. Although traditional optimization techniques, such as stochastic and robust optimization approaches, could be used to address the OPF problem in the face of renewable energy uncertainty, their effectiveness in dealing with large-scale problems remains limited. As a result, deep learning techniques, such as neural networks, have recently been developed to improve computational efficiency in solving large-scale OPF problems. However, the feasibility and optimality of the solution may not be guaranteed. In this paper, we propose an optimization model-informed generative adversarial network (MI-GAN) framework to solve OPF under uncertainty. The main contributions are summarized into three aspects: (1) to ensure feasibility and improve optimality of generated solutions, three important layers are proposed: feasibility filter layer, comparison layer, and gradient-guided layer; (2) in the GAN-based framework, an efficient model-informed selector incorporating these three new layers is established; and (3) a new recursive iteration algorithm is also proposed to improve solution optimality. The numerical results on IEEE test systems show that the proposed method is very effective and promising.

Optimistic Distributionally Robust Policy Optimization

Trust Region Policy Optimization (TRPO) and Proximal Policy Optimization (PPO), as the widely employed policy based reinforcement learning (RL) methods, are prone to converge to a sub-optimal solution as they limit the policy representation to a particular parametric distribution class. To address this issue, we develop an innovative Optimistic Distributionally Robust Policy Optimization (ODRPO) algorithm, which effectively utilizes Optimistic Distributionally Robust Optimization (DRO) approach to solve the trust region constrained optimization problem without parameterizing the policies. Our algorithm improves TRPO and PPO with a higher sample efficiency and a better performance of the final policy while attaining the learning stability. Moreover, it achieves a globally optimal policy update that is not promised in the prevailing policy based RL algorithms. Experiments across tabular domains and robotic locomotion tasks demonstrate the effectiveness of our approach.