CASP: Few-Shot Class-Incremental Learning with CLS Token Attention Steering Prompts

Few-shot class-incremental learning (FSCIL) presents a core challenge in continual learning, requiring models to rapidly adapt to new classes with very limited samples while mitigating catastrophic forgetting. Recent prompt-based methods, which integrate pretrained backbones with task-specific prompts, have made notable progress. However, under extreme few-shot incremental settings, the model's ability to transfer and generalize becomes critical, and it is thus essential to leverage pretrained knowledge to learn feature representations that can be shared across future categories during the base session. Inspired by the mechanism of the CLS token, which is similar to human attention and progressively filters out task-irrelevant information, we propose the CLS Token Attention Steering Prompts (CASP). This approach introduces class-shared trainable bias parameters into the query, key, and value projections of the CLS token to explicitly modulate the self-attention weights. To further enhance generalization, we also design an attention perturbation strategy and perform Manifold Token Mixup in the shallow feature space, synthesizing potential new class features to improve generalization and reserve the representation capacity for upcoming tasks. Experiments on the CUB200, CIFAR100, and ImageNet-R datasets demonstrate that CASP outperforms state-of-the-art methods in both standard and fine-grained FSCIL settings without requiring fine-tuning during incremental phases and while significantly reducing the parameter overhead.

HUMANLLM: Benchmarking and Reinforcing LLM Anthropomorphism via Human Cognitive Patterns

Large Language Models (LLMs) have demonstrated remarkable capabilities in reasoning and generation, serving as the foundation for advanced persona simulation and Role-Playing Language Agents (RPLAs). However, achieving authentic alignment with human cognitive and behavioral patterns remains a critical challenge for these agents. We present HUMANLLM, a framework treating psychological patterns as interacting causal forces. We construct 244 patterns from ~12,000 academic papers and synthesize 11,359 scenarios where 2-5 patterns reinforce, conflict, or modulate each other, with multi-turn conversations expressing inner thoughts, actions, and dialogue. Our dual-level checklists evaluate both individual pattern fidelity and emergent multi-pattern dynamics, achieving strong human alignment (r=0.91) while revealing that holistic metrics conflate simulation accuracy with social desirability. HUMANLLM-8B outperforms Qwen3-32B on multi-pattern dynamics despite 4x fewer parameters, demonstrating that authentic anthropomorphism requires cognitive modeling--simulating not just what humans do, but the psychological processes generating those behaviors.

SmartHome-Bench: A Comprehensive Benchmark for Video Anomaly Detection in Smart Homes Using Multi-Modal Large Language Models

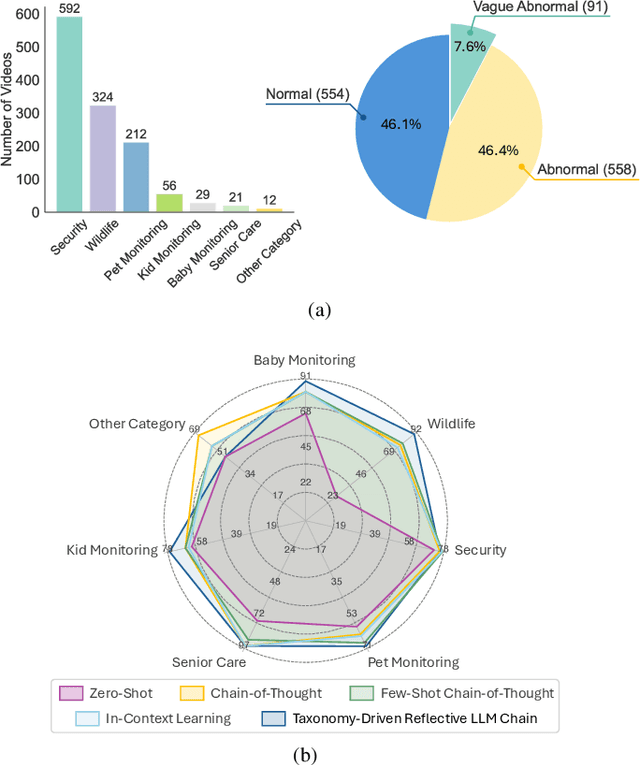
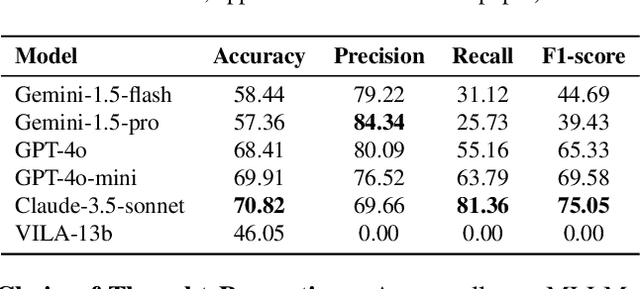
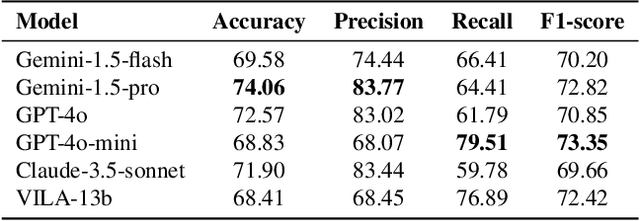
Video anomaly detection (VAD) is essential for enhancing safety and security by identifying unusual events across different environments. Existing VAD benchmarks, however, are primarily designed for general-purpose scenarios, neglecting the specific characteristics of smart home applications. To bridge this gap, we introduce SmartHome-Bench, the first comprehensive benchmark specially designed for evaluating VAD in smart home scenarios, focusing on the capabilities of multi-modal large language models (MLLMs). Our newly proposed benchmark consists of 1,203 videos recorded by smart home cameras, organized according to a novel anomaly taxonomy that includes seven categories, such as Wildlife, Senior Care, and Baby Monitoring. Each video is meticulously annotated with anomaly tags, detailed descriptions, and reasoning. We further investigate adaptation methods for MLLMs in VAD, assessing state-of-the-art closed-source and open-source models with various prompting techniques. Results reveal significant limitations in the current models' ability to detect video anomalies accurately. To address these limitations, we introduce the Taxonomy-Driven Reflective LLM Chain (TRLC), a new LLM chaining framework that achieves a notable 11.62% improvement in detection accuracy. The benchmark dataset and code are publicly available at https://github.com/Xinyi-0724/SmartHome-Bench-LLM.

Improving the Test-retest Reliability of Quantitative Susceptibility Mapping

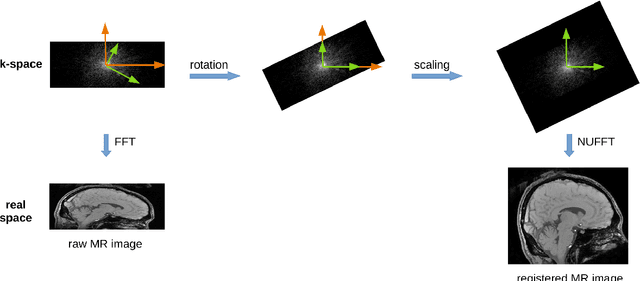
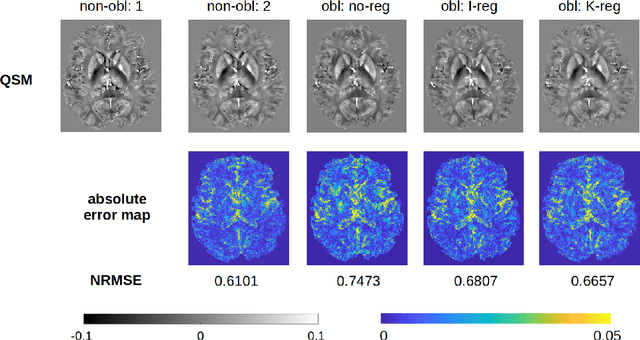
Motivation - The test-retest reliability of quantitative susceptibility mapping (QSM) is affected by parameters of the acquisition protocol such as the angulation of acquisition plane with respect to the B0 field direction and spatial resolution. Goal - We aim to reduce the protocol-dependent biases/errors that might overshadow subtle changes of the susceptibility values due to pathology in the brain. Approach - The magnitude and phase images used for QSM are registered according to a standard reference protocol in the k-space through nonuniform fast Fourier transform (NUFFT). Results - With the help of our proposed approach, the test-retest reliability of scans acquired from different protocols is notably improved. Impact - The improved test-retest reliability of QSM makes it easier to detect subtle susceptibility changes in the early stages of neurodegeneration such as Alzheimer's disease and Parkinson's disease.

Solving Quadratic Systems with Full-Rank Matrices Using Sparse or Generative Priors

The problem of recovering a signal $\boldsymbol{x} \in \mathbb{R}^n$ from a quadratic system $\{y_i=\boldsymbol{x}^\top\boldsymbol{A}_i\boldsymbol{x},\ i=1,\ldots,m\}$ with full-rank matrices $\boldsymbol{A}_i$ frequently arises in applications such as unassigned distance geometry and sub-wavelength imaging. With i.i.d. standard Gaussian matrices $\boldsymbol{A}_i$, this paper addresses the high-dimensional case where $m\ll n$ by incorporating prior knowledge of $\boldsymbol{x}$. First, we consider a $k$-sparse $\boldsymbol{x}$ and introduce the thresholded Wirtinger flow (TWF) algorithm that does not require the sparsity level $k$. TWF comprises two steps: the spectral initialization that identifies a point sufficiently close to $\boldsymbol{x}$ (up to a sign flip) when $m=O(k^2\log n)$, and the thresholded gradient descent (with a good initialization) that produces a sequence linearly converging to $\boldsymbol{x}$ with $m=O(k\log n)$ measurements. Second, we explore the generative prior, assuming that $\boldsymbol{x}$ lies in the range of an $L$-Lipschitz continuous generative model with $k$-dimensional inputs in an $\ell_2$-ball of radius $r$. We develop the projected gradient descent (PGD) algorithm that also comprises two steps: the projected power method that provides an initial vector with $O\big(\sqrt{\frac{k \log L}{m}}\big)$ $\ell_2$-error given $m=O(k\log(Lnr))$ measurements, and the projected gradient descent that refines the $\ell_2$-error to $O(\delta)$ at a geometric rate when $m=O(k\log\frac{Lrn}{\delta^2})$. Experimental results corroborate our theoretical findings and show that: (i) our approach for the sparse case notably outperforms the existing provable algorithm sparse power factorization; (ii) leveraging the generative prior allows for precise image recovery in the MNIST dataset from a small number of quadratic measurements.

AIDE: A Vision-Driven Multi-View, Multi-Modal, Multi-Tasking Dataset for Assistive Driving Perception

Driver distraction has become a significant cause of severe traffic accidents over the past decade. Despite the growing development of vision-driven driver monitoring systems, the lack of comprehensive perception datasets restricts road safety and traffic security. In this paper, we present an AssIstive Driving pErception dataset (AIDE) that considers context information both inside and outside the vehicle in naturalistic scenarios. AIDE facilitates holistic driver monitoring through three distinctive characteristics, including multi-view settings of driver and scene, multi-modal annotations of face, body, posture, and gesture, and four pragmatic task designs for driving understanding. To thoroughly explore AIDE, we provide experimental benchmarks on three kinds of baseline frameworks via extensive methods. Moreover, two fusion strategies are introduced to give new insights into learning effective multi-stream/modal representations. We also systematically investigate the importance and rationality of the key components in AIDE and benchmarks. The project link is https://github.com/ydk122024/AIDE.

Joint Recovery of T1, T2* and Proton Density Maps Using a Bayesian Approach with Parameter Estimation and Complementary Undersampling Patterns

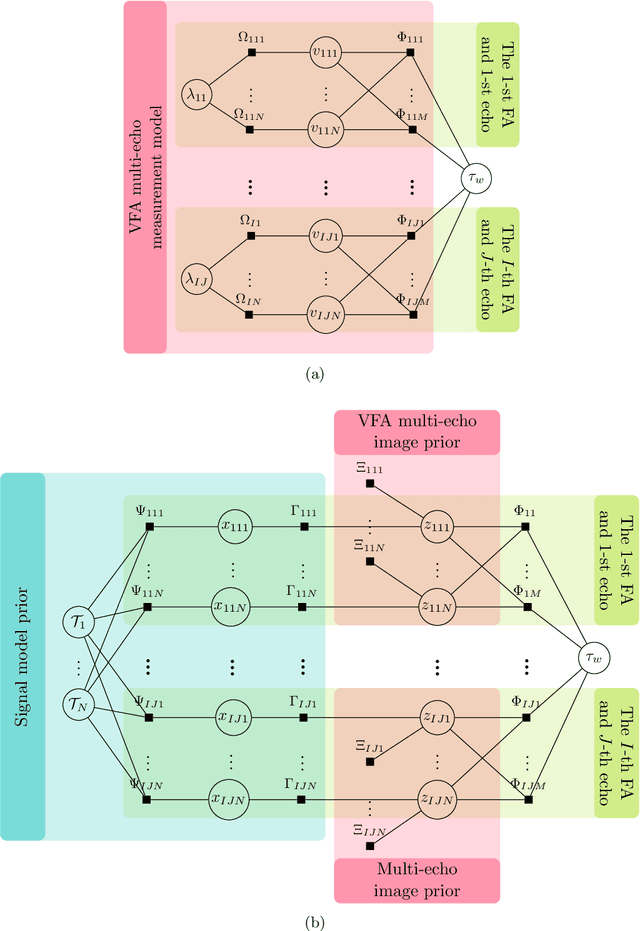
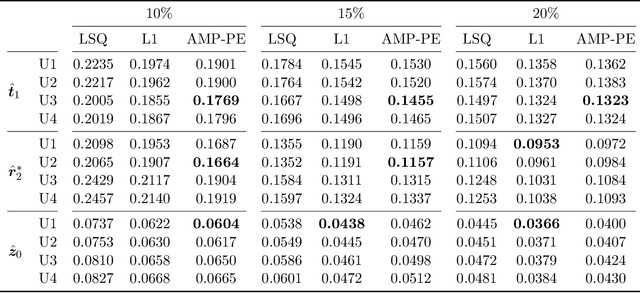
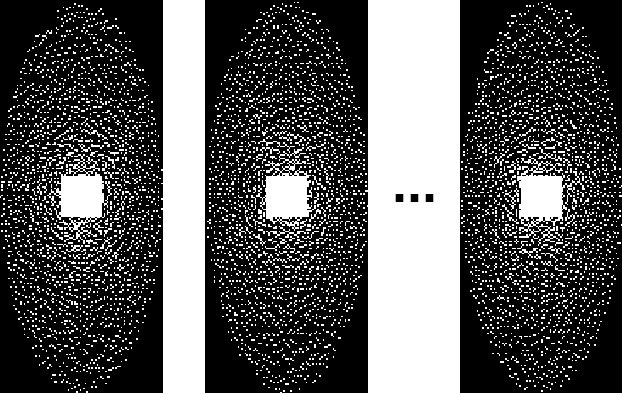
Purpose: To improve the quality of quantitative MR images recovered from undersampled measurements, we incorporate the signal model of the variable-flip-angle (VFA) multi-echo 3D gradient-echo (GRE) method into the reconstruction of $T_1$, $T_2^*$ and proton density (PD) maps. Additionally, we investigate the use of complementary undersampling patterns to determine optimal undersampling schemes for quantitative MRI. Theory: We propose a probabilistic Bayesian formulation of the recovery problem. Our proposed approach, approximate message passing with built-in parameter estimation (AMP-PE), enables the joint recovery of distribution parameters, VFA multi-echo images, and $T_1$, $T_2^*$, and PD maps without the need for hyperparameter tuning. Methods: We conducted both retrospective and prospective undersampling to obtain Fourier measurements using variable-density and Poisson-disk patterns. We investigated a variety of undersampling schemes, adopting complementary patterns across different flip angles and/or echo times. Results: AMP-PE adopts a joint recovery strategy, it outperforms the state-of-the-art $l1$-norm minimization approach that follows a decoupled recovery strategy. For $T_1$ mapping, employing fixed sampling patterns across different echo times produced the best performance. Whereas for $T_2^*$ and proton density mappings, using complementary sampling patterns across different flip angles yielded the best performance. Conclusion: AMP-PE achieves better performance by combining information from both the MR signal model and the sparse prior on VFA multi-echo images. It is equipped with automatic and adaptive parameter estimation, and works naturally with the clinical prospective undersampling scheme.

Context De-confounded Emotion Recognition

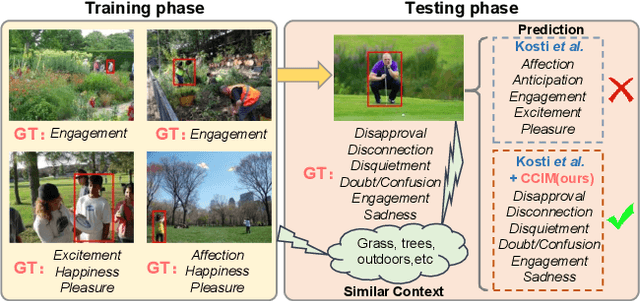
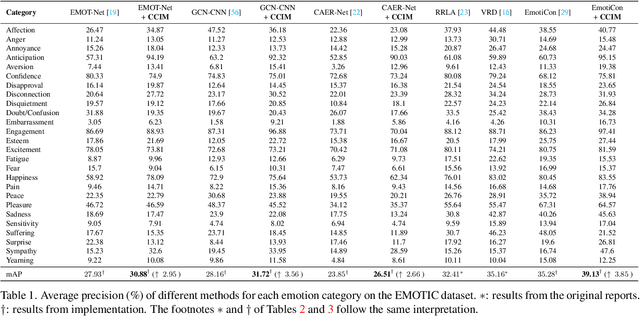
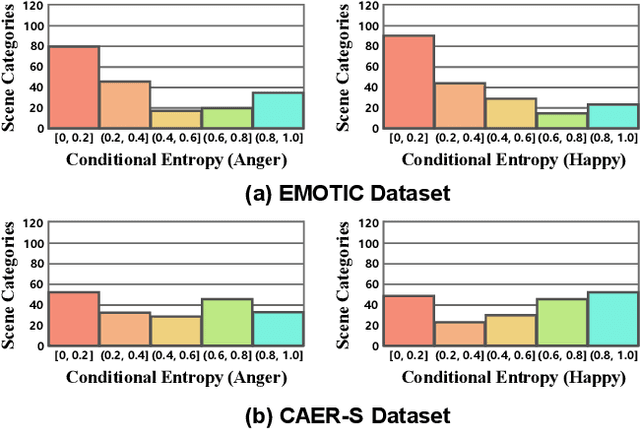
Context-Aware Emotion Recognition (CAER) is a crucial and challenging task that aims to perceive the emotional states of the target person with contextual information. Recent approaches invariably focus on designing sophisticated architectures or mechanisms to extract seemingly meaningful representations from subjects and contexts. However, a long-overlooked issue is that a context bias in existing datasets leads to a significantly unbalanced distribution of emotional states among different context scenarios. Concretely, the harmful bias is a confounder that misleads existing models to learn spurious correlations based on conventional likelihood estimation, significantly limiting the models' performance. To tackle the issue, this paper provides a causality-based perspective to disentangle the models from the impact of such bias, and formulate the causalities among variables in the CAER task via a tailored causal graph. Then, we propose a Contextual Causal Intervention Module (CCIM) based on the backdoor adjustment to de-confound the confounder and exploit the true causal effect for model training. CCIM is plug-in and model-agnostic, which improves diverse state-of-the-art approaches by considerable margins. Extensive experiments on three benchmark datasets demonstrate the effectiveness of our CCIM and the significance of causal insight.

DynImp: Dynamic Imputation for Wearable Sensing Data Through Sensory and Temporal Relatedness

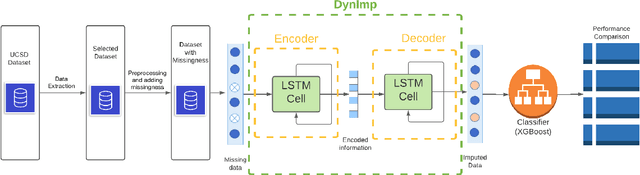
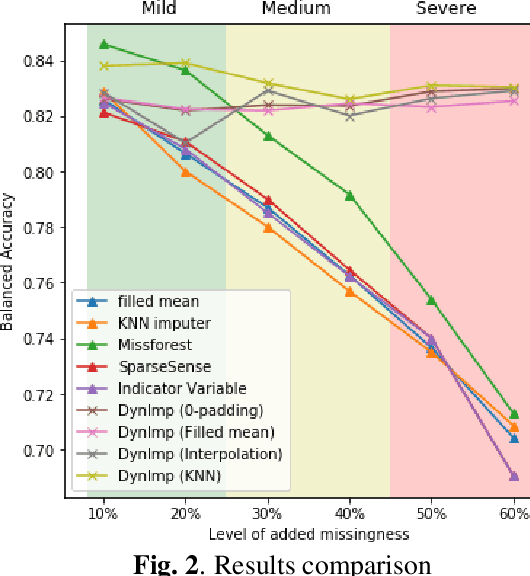
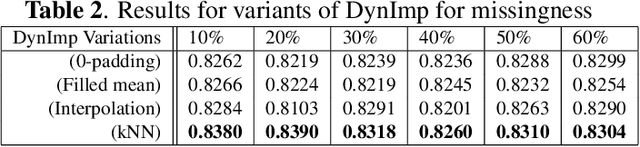
In wearable sensing applications, data is inevitable to be irregularly sampled or partially missing, which pose challenges for any downstream application. An unique aspect of wearable data is that it is time-series data and each channel can be correlated to another one, such as x, y, z axis of accelerometer. We argue that traditional methods have rarely made use of both times-series dynamics of the data as well as the relatedness of the features from different sensors. We propose a model, termed as DynImp, to handle different time point's missingness with nearest neighbors along feature axis and then feeding the data into a LSTM-based denoising autoencoder which can reconstruct missingness along the time axis. We experiment the model on the extreme missingness scenario ($>50\%$ missing rate) which has not been widely tested in wearable data. Our experiments on activity recognition show that the method can exploit the multi-modality features from related sensors and also learn from history time-series dynamics to reconstruct the data under extreme missingness.

Density-Aware Personalized Training for Risk Prediction in Imbalanced Medical Data

Medical events of interest, such as mortality, often happen at a low rate in electronic medical records, as most admitted patients survive. Training models with this imbalance rate (class density discrepancy) may lead to suboptimal prediction. Traditionally this problem is addressed through ad-hoc methods such as resampling or reweighting but performance in many cases is still limited. We propose a framework for training models for this imbalance issue: 1) we first decouple the feature extraction and classification process, adjusting training batches separately for each component to mitigate bias caused by class density discrepancy; 2) we train the network with both a density-aware loss and a learnable cost matrix for misclassifications. We demonstrate our model's improved performance in real-world medical datasets (TOPCAT and MIMIC-III) to show improved AUC-ROC, AUC-PRC, Brier Skill Score compared with the baselines in the domain.