Joint Recovery of T1, T2* and Proton Density Maps Using a Bayesian Approach with Parameter Estimation and Complementary Undersampling Patterns

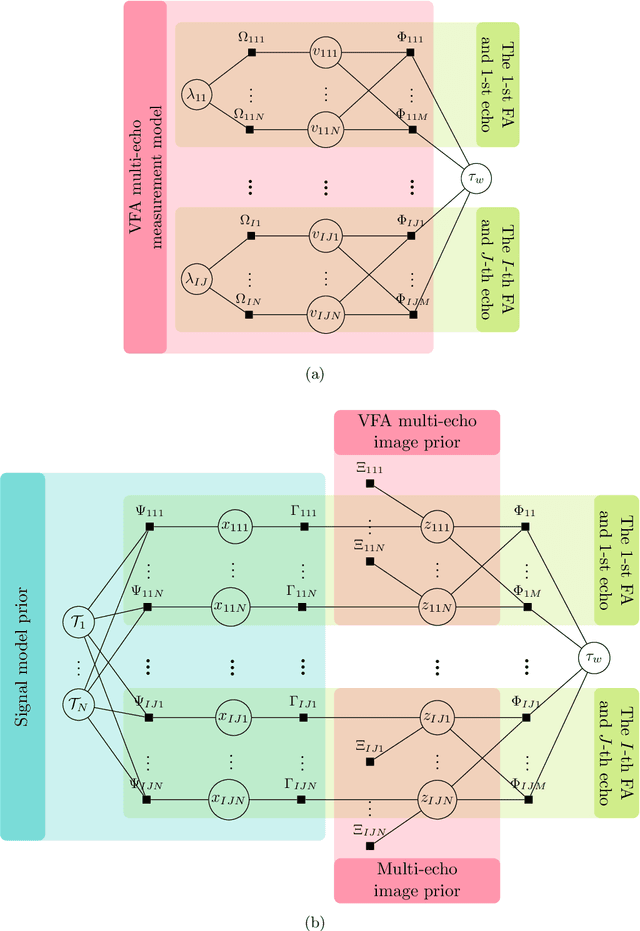
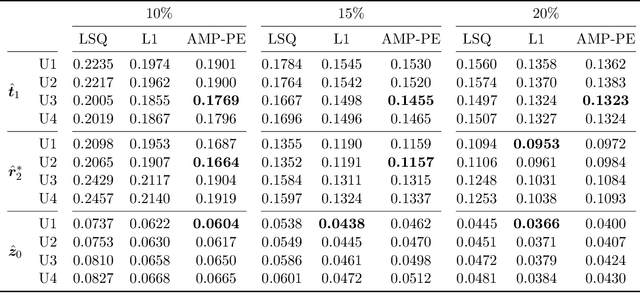
Purpose: To improve the quality of quantitative MR images recovered from undersampled measurements, we incorporate the signal model of the variable-flip-angle (VFA) multi-echo 3D gradient-echo (GRE) method into the reconstruction of $T_1$, $T_2^*$ and proton density (PD) maps. Additionally, we investigate the use of complementary undersampling patterns to determine optimal undersampling schemes for quantitative MRI. Theory: We propose a probabilistic Bayesian formulation of the recovery problem. Our proposed approach, approximate message passing with built-in parameter estimation (AMP-PE), enables the joint recovery of distribution parameters, VFA multi-echo images, and $T_1$, $T_2^*$, and PD maps without the need for hyperparameter tuning. Methods: We conducted both retrospective and prospective undersampling to obtain Fourier measurements using variable-density and Poisson-disk patterns. We investigated a variety of undersampling schemes, adopting complementary patterns across different flip angles and/or echo times. Results: AMP-PE adopts a joint recovery strategy, it outperforms the state-of-the-art $l1$-norm minimization approach that follows a decoupled recovery strategy. For $T_1$ mapping, employing fixed sampling patterns across different echo times produced the best performance. Whereas for $T_2^*$ and proton density mappings, using complementary sampling patterns across different flip angles yielded the best performance. Conclusion: AMP-PE achieves better performance by combining information from both the MR signal model and the sparse prior on VFA multi-echo images. It is equipped with automatic and adaptive parameter estimation, and works naturally with the clinical prospective undersampling scheme.

Robust Quantitative Susceptibility Mapping via Approximate Message Passing

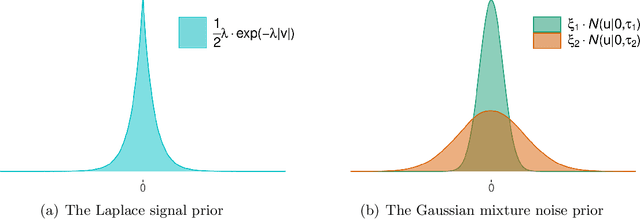
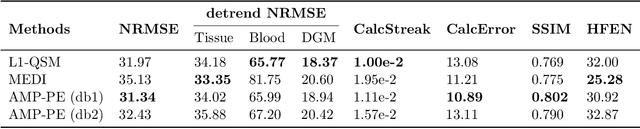
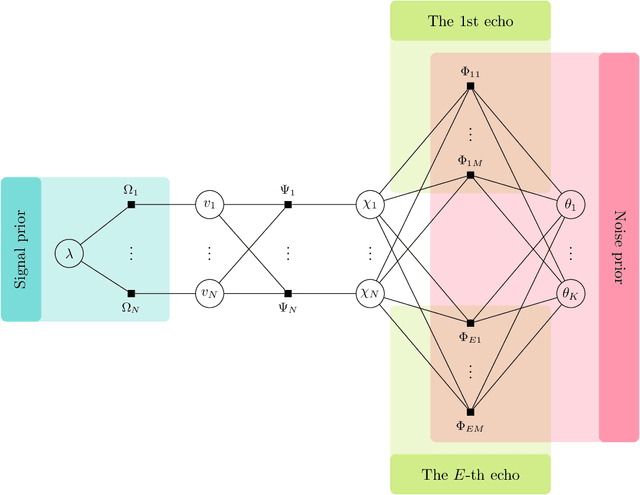
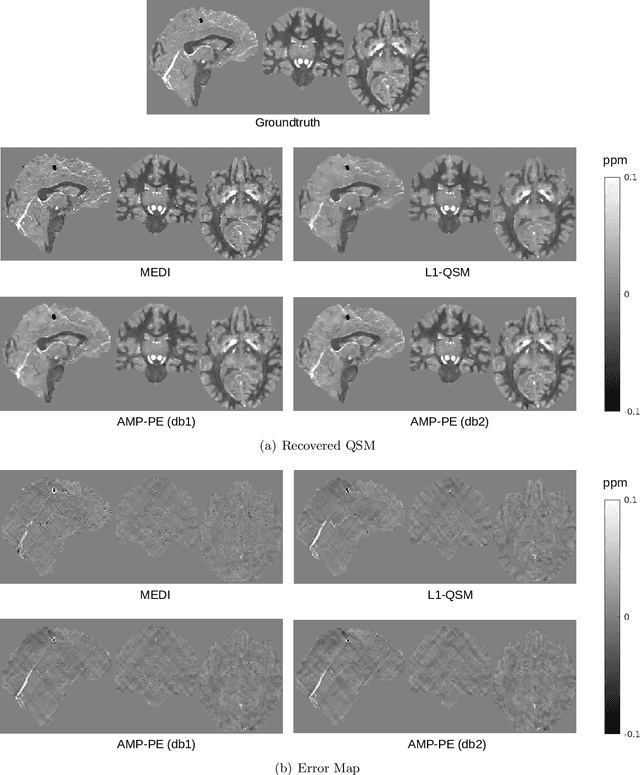
Purpose: It has been challenging to recover QSM in the presence of phase errors, which could be caused by the noise or strong local susceptibility shifts in cases of brain hemorrhage and calcification. We propose a Bayesian formulation for QSM where a two-component Gaussian-mixture distribution is used to model the long-tailed noise (error) distribution, and design an approximate message passing (AMP) algorithm with automatic and adaptive parameter estimation. Theory: Wavelet coefficients of the susceptibility map follow the Laplace distribution. The measurement noise follows a two-component Gaussian-mixture distribution where the second Gaussian component models the noise outliers. The distribution parameters are treated as unknown variables and jointly recovered with the susceptibility using AMP. Methods: The proposed AMP with parameter estimation (AMP-PE) is compared with the state-of-the-art nonlinear L1-QSM and MEDI approaches that adopt the L1-norm and L2-norm data-fidelity terms respectively. The three approaches are tested on the Sim2Snr1 data from QSM challenge 2.0, the in vivo data from both healthy and hemorrhage scans. Results: On the simulated Sim2Snr1 dataset, AMP-PE achieved the lowest NRMSE and SSIM, MEDI achieved the lowest HFEN, and each approach also has its own strong suit when it comes to various local evaluation metrics. On the in vivo dataset, AMP-PE is better at preserving structural details and removing streaking artifacts than L1-QSM and MEDI. Conclusion: By leveraging a customized Gaussian-mixture noise prior, AMP-PE achieves better performance on the challenging QSM cases involving hemorrhage and calcification. It is equipped with built-in parameter estimation, which avoids subjective bias from the usual visual fine-tuning step of in vivo reconstruction.

A Bayesian approach for $T_2^*$ Mapping and Quantitative Susceptibility Mapping

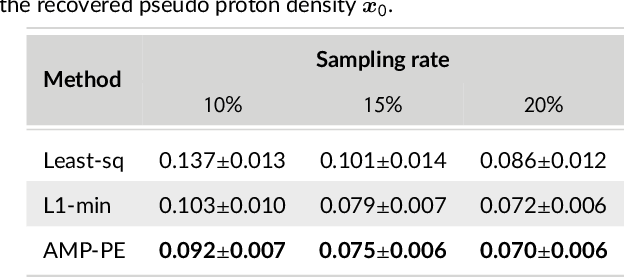
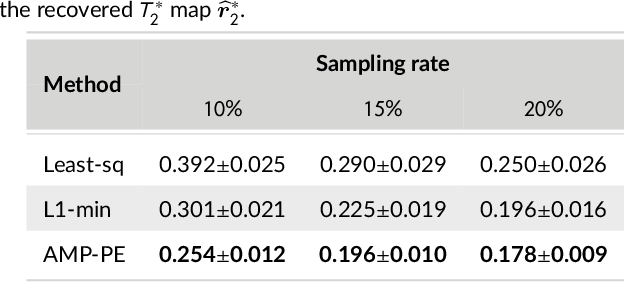
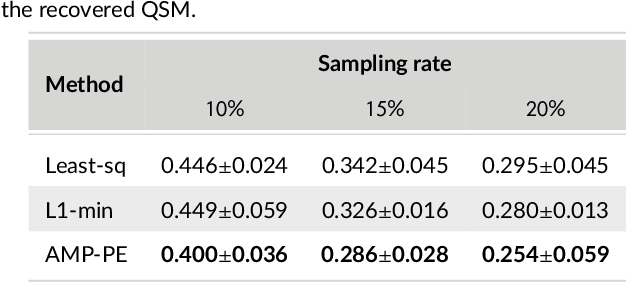
Magnetic resonance $T_2^*$ mapping and quantitative susceptibility mapping (QSM) provide direct and precise mappings of tissue contrasts. They are widely used to study iron deposition, hemorrhage and calcification in various clinical applications. In practice, the measurements can be undersampled in the $k$-space to reduce the scan time needed for high-resolution 3D maps, and sparse prior on the wavelet coefficients of images can be used to fill in the missing information via compressive sensing. To avoid the extensive parameter tuning process of conventional regularization methods, we adopt a Bayesian approach to perform $T_2^*$ mapping and QSM using approximate message passing (AMP): the sparse prior is enforced through probability distributions, and the distribution parameters can be automatically and adaptively estimated. In this paper we propose a new nonlinear AMP framework that incorporates the mono-exponential decay model, and use it to recover the proton density, the $T_2^*$ map and complex multi-echo images. The QSM can be computed from the multi-echo images subsequently. Experimental results show that the proposed approach successfully recovers $T_2^*$ map and QSM across various sampling rates, and performs much better than the state-of-the-art $l_1$-norm regularization approach.

Fast Nonconvex $T_2^*$ Mapping Using ADMM

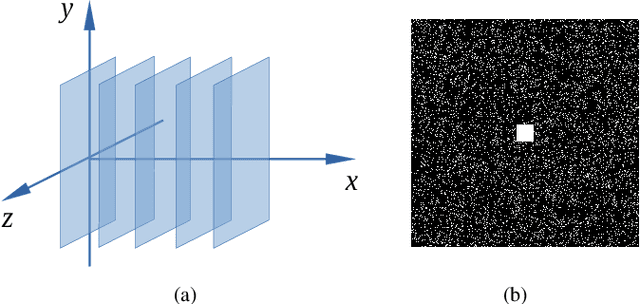
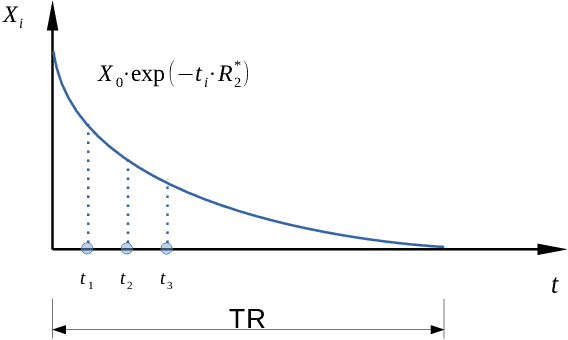
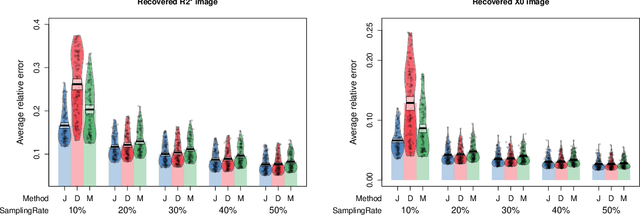
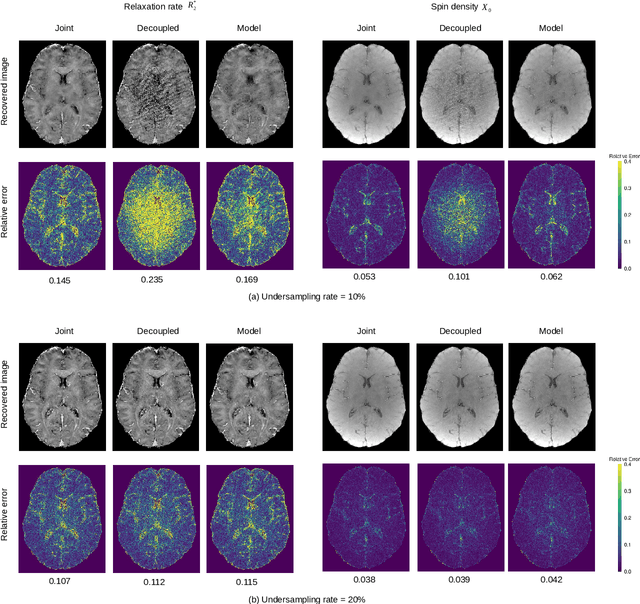
Magnetic resonance (MR)-$T_2^*$ mapping is widely used to study hemorrhage, calcification and iron deposition in various clinical applications, it provides a direct and precise mapping of desired contrast in the tissue. However, the long acquisition time required by conventional 3D high-resolution $T_2^*$ mapping method causes discomfort to patients and introduces motion artifacts to reconstructed images, which limits its wider applicability. In this paper we address this issue by performing $T_2^*$ mapping from undersampled data using compressive sensing (CS). We formulate the reconstruction as a nonconvex problem that can be decomposed into two subproblems. They can be solved either separately via the standard approach or jointly via the alternating direction method of multipliers (ADMM). Compared to previous CS-based approaches that only apply sparse regularization on the spin density $\boldsymbol X_0$ and the relaxation rate $\boldsymbol R_2^*$, our formulation enforces additional sparse priors on the $T_2^*$-weighted images at multiple echoes to improve the reconstruction performance. We performed convergence analysis of the proposed algorithm, evaluated its performance on in vivo data, and studied the effects of different sampling schemes. Experimental results showed that the proposed joint-recovery approach generally outperforms the state-of-the-art method, especially in the low-sampling rate regime, making it a preferred choice to perform fast 3D $T_2^*$ mapping in practice. The framework adopted in this work can be easily extended to other problems arising from MR or other imaging modalities with non-linearly coupled variables.