Deqiang Qiu
Improving the Test-retest Reliability of Quantitative Susceptibility Mapping
Nov 15, 2024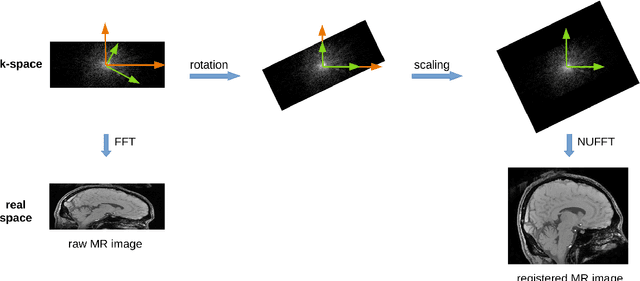
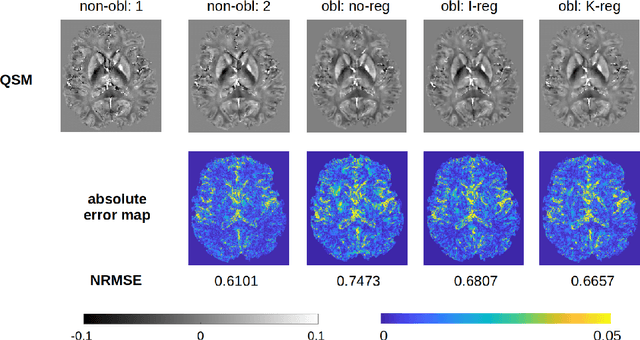
Abstract:Motivation - The test-retest reliability of quantitative susceptibility mapping (QSM) is affected by parameters of the acquisition protocol such as the angulation of acquisition plane with respect to the B0 field direction and spatial resolution. Goal - We aim to reduce the protocol-dependent biases/errors that might overshadow subtle changes of the susceptibility values due to pathology in the brain. Approach - The magnitude and phase images used for QSM are registered according to a standard reference protocol in the k-space through nonuniform fast Fourier transform (NUFFT). Results - With the help of our proposed approach, the test-retest reliability of scans acquired from different protocols is notably improved. Impact - The improved test-retest reliability of QSM makes it easier to detect subtle susceptibility changes in the early stages of neurodegeneration such as Alzheimer's disease and Parkinson's disease.
Motion and temporal B0 shift corrections for quantitative susceptibility mapping and R2* mapping using dual-echo spiral navigators and conjugate-phase reconstruction
Mar 18, 2024Abstract:Purpose: To develop an efficient navigator-based motion and temporal B0 shift correction technique for 3D multi-echo gradient-echo (ME-GRE) MRI for quantitative susceptibility mapping (QSM) and R2* mapping. Theory and Methods: A dual-echo 3D spiral navigator was designed to interleave with the Cartesian ME-GRE acquisitions, allowing the acquisition of both low- and high-echo time signals. We additionally designed a novel conjugate-phase based reconstruction method for the joint correction of motion and temporal B0 shifts. We performed both numerical simulation and in vivo human scans to assess the performance of the methods. Results: Numerical simulation and human brain scans demonstrated that the proposed technique successfully corrected artifacts induced by both head motions and temporal B0 changes. Efficient B0-change correction with conjugate-phase reconstruction can be performed on less than 10 clustered k-space segments. In vivo scans showed that combining temporal B0 correction with motion correction further reduced artifacts and improved image quality in both R2* and QSM images. Conclusion: Our proposed approach of using 3D spiral navigators and a novel conjugate-phase reconstruction method can improve susceptibility-related measurements using MR.
Joint Recovery of T1, T2* and Proton Density Maps Using a Bayesian Approach with Parameter Estimation and Complementary Undersampling Patterns
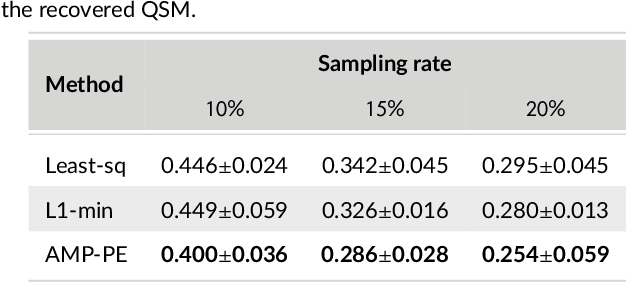
Jul 05, 2023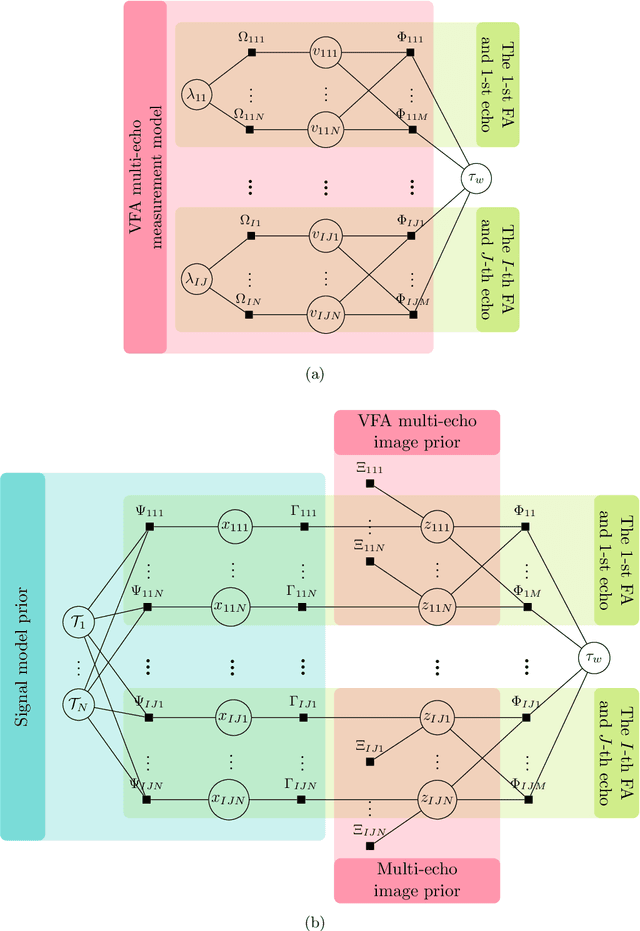
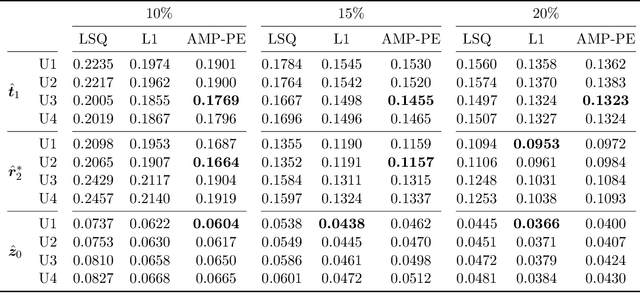
Abstract:Purpose: To improve the quality of quantitative MR images recovered from undersampled measurements, we incorporate the signal model of the variable-flip-angle (VFA) multi-echo 3D gradient-echo (GRE) method into the reconstruction of $T_1$, $T_2^*$ and proton density (PD) maps. Additionally, we investigate the use of complementary undersampling patterns to determine optimal undersampling schemes for quantitative MRI. Theory: We propose a probabilistic Bayesian formulation of the recovery problem. Our proposed approach, approximate message passing with built-in parameter estimation (AMP-PE), enables the joint recovery of distribution parameters, VFA multi-echo images, and $T_1$, $T_2^*$, and PD maps without the need for hyperparameter tuning. Methods: We conducted both retrospective and prospective undersampling to obtain Fourier measurements using variable-density and Poisson-disk patterns. We investigated a variety of undersampling schemes, adopting complementary patterns across different flip angles and/or echo times. Results: AMP-PE adopts a joint recovery strategy, it outperforms the state-of-the-art $l1$-norm minimization approach that follows a decoupled recovery strategy. For $T_1$ mapping, employing fixed sampling patterns across different echo times produced the best performance. Whereas for $T_2^*$ and proton density mappings, using complementary sampling patterns across different flip angles yielded the best performance. Conclusion: AMP-PE achieves better performance by combining information from both the MR signal model and the sparse prior on VFA multi-echo images. It is equipped with automatic and adaptive parameter estimation, and works naturally with the clinical prospective undersampling scheme.
Concentric Tube Robot Redundancy Resolution via Velocity/Compliance Manipulability Optimization
May 10, 2023Abstract:Concentric Tube Robots (CTR) have the potential to enable effective minimally invasive surgeries. While extensive modeling and control schemes have been proposed in the past decade, limited efforts have been made to improve the trajectory tracking performance from the perspective of manipulability , which can be critical to generate safe motion and feasible actuator commands. In this paper, we propose a gradient-based redundancy resolution framework that optimizes velocity/compliance manipulability-based performance indices during trajectory tracking for a kinematically redundant CTR. We efficiently calculate the gradients of manipulabilities by propagating the first- and second-order derivatives of state variables of the Cosserat rod model along the CTR arc length, reducing the gradient computation time by 68\% compared to finite difference method. Task-specific performance indices are optimized by projecting the gradient into the null-space of trajectory tracking. The proposed method is validated in three exemplary scenarios that involve trajectory tracking, obstacle avoidance, and external load compensation, respectively. Simulation results show that the proposed method is able to accomplish the required tasks while commonly used redundancy resolution approaches underperform or even fail.
Robust Quantitative Susceptibility Mapping via Approximate Message Passing
Jul 29, 2022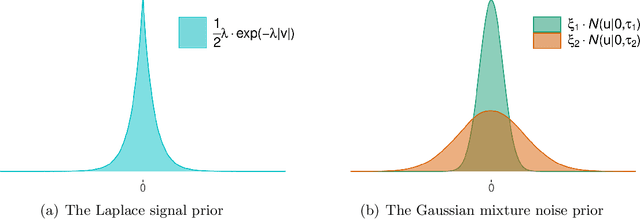
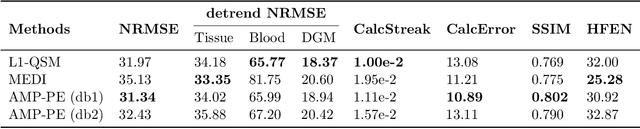
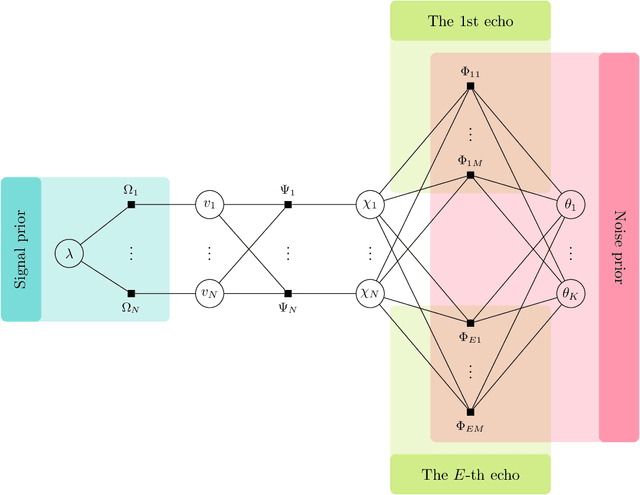
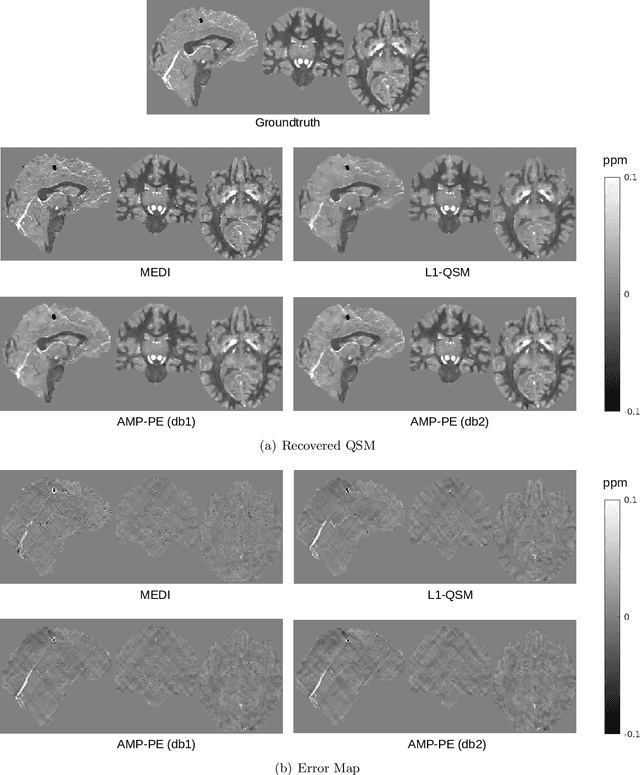
Abstract:Purpose: It has been challenging to recover QSM in the presence of phase errors, which could be caused by the noise or strong local susceptibility shifts in cases of brain hemorrhage and calcification. We propose a Bayesian formulation for QSM where a two-component Gaussian-mixture distribution is used to model the long-tailed noise (error) distribution, and design an approximate message passing (AMP) algorithm with automatic and adaptive parameter estimation. Theory: Wavelet coefficients of the susceptibility map follow the Laplace distribution. The measurement noise follows a two-component Gaussian-mixture distribution where the second Gaussian component models the noise outliers. The distribution parameters are treated as unknown variables and jointly recovered with the susceptibility using AMP. Methods: The proposed AMP with parameter estimation (AMP-PE) is compared with the state-of-the-art nonlinear L1-QSM and MEDI approaches that adopt the L1-norm and L2-norm data-fidelity terms respectively. The three approaches are tested on the Sim2Snr1 data from QSM challenge 2.0, the in vivo data from both healthy and hemorrhage scans. Results: On the simulated Sim2Snr1 dataset, AMP-PE achieved the lowest NRMSE and SSIM, MEDI achieved the lowest HFEN, and each approach also has its own strong suit when it comes to various local evaluation metrics. On the in vivo dataset, AMP-PE is better at preserving structural details and removing streaking artifacts than L1-QSM and MEDI. Conclusion: By leveraging a customized Gaussian-mixture noise prior, AMP-PE achieves better performance on the challenging QSM cases involving hemorrhage and calcification. It is equipped with built-in parameter estimation, which avoids subjective bias from the usual visual fine-tuning step of in vivo reconstruction.
Approximate Message Passing with Parameter Estimation for Heavily Quantized Measurements
May 20, 2022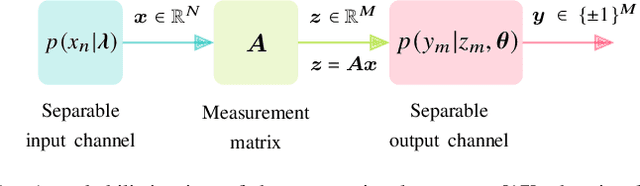
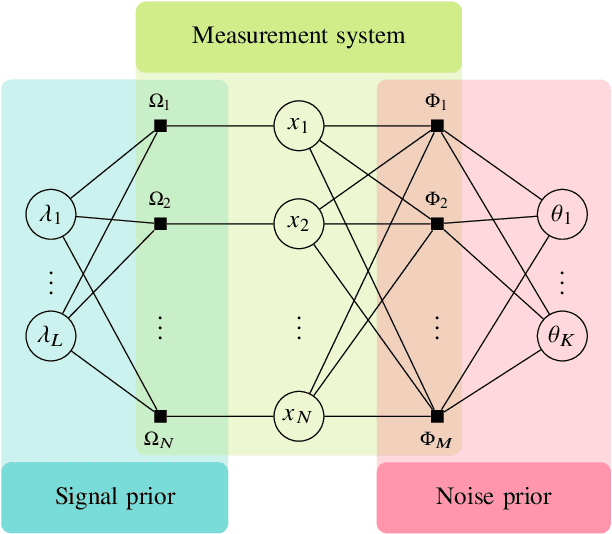
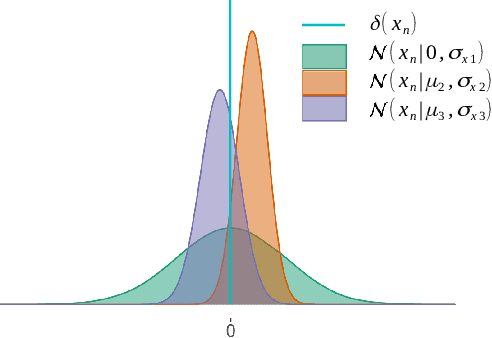
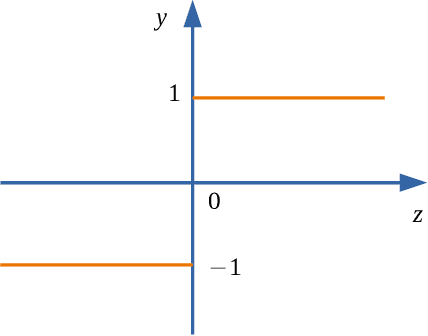
Abstract:Designing efficient sparse recovery algorithms that could handle noisy quantized measurements is important in a variety of applications -- from radar to source localization, spectrum sensing and wireless networking. We take advantage of the approximate message passing (AMP) framework to achieve this goal given its high computational efficiency and state-of-the-art performance. In AMP, the signal of interest is assumed to follow certain prior distribution with unknown parameters. Previous works focused on finding the parameters that maximize the measurement likelihood via expectation maximization -- an increasingly difficult problem to solve in cases involving complicated probability models. In this paper, we treat the parameters as unknown variables and compute their posteriors via AMP. The parameters and signal of interest can then be jointly recovered. Compared to previous methods, the proposed approach leads to a simple and elegant parameter estimation scheme, allowing us to directly work with 1-bit quantization noise model. We then further extend our approach to general multi-bit quantization noise model. Experimental results show that the proposed framework provides significant improvement over state-of-the-art methods across a wide range of sparsity and noise levels.
* arXiv admin note: text overlap with arXiv:2007.07679
A Bayesian approach for $T_2^*$ Mapping and Quantitative Susceptibility Mapping
Mar 09, 2021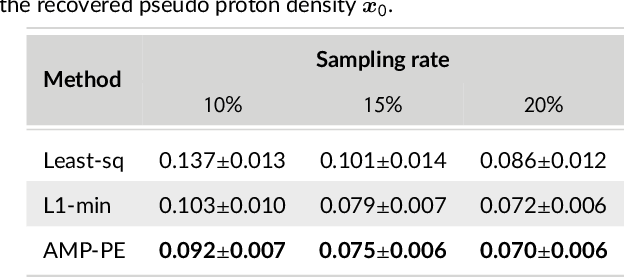
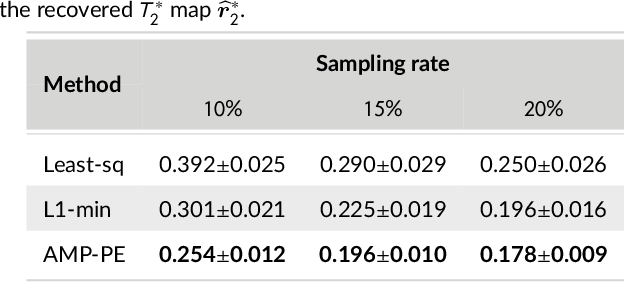
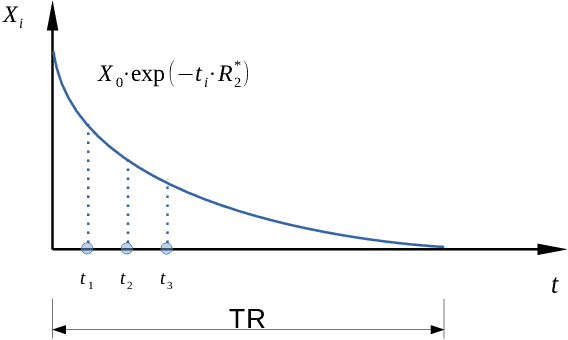
Abstract:Magnetic resonance $T_2^*$ mapping and quantitative susceptibility mapping (QSM) provide direct and precise mappings of tissue contrasts. They are widely used to study iron deposition, hemorrhage and calcification in various clinical applications. In practice, the measurements can be undersampled in the $k$-space to reduce the scan time needed for high-resolution 3D maps, and sparse prior on the wavelet coefficients of images can be used to fill in the missing information via compressive sensing. To avoid the extensive parameter tuning process of conventional regularization methods, we adopt a Bayesian approach to perform $T_2^*$ mapping and QSM using approximate message passing (AMP): the sparse prior is enforced through probability distributions, and the distribution parameters can be automatically and adaptively estimated. In this paper we propose a new nonlinear AMP framework that incorporates the mono-exponential decay model, and use it to recover the proton density, the $T_2^*$ map and complex multi-echo images. The QSM can be computed from the multi-echo images subsequently. Experimental results show that the proposed approach successfully recovers $T_2^*$ map and QSM across various sampling rates, and performs much better than the state-of-the-art $l_1$-norm regularization approach.
Fast Nonconvex $T_2^*$ Mapping Using ADMM
Aug 04, 2020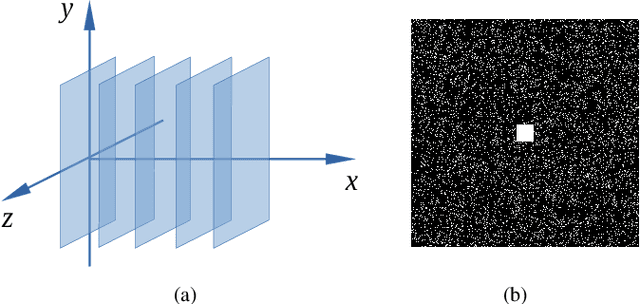
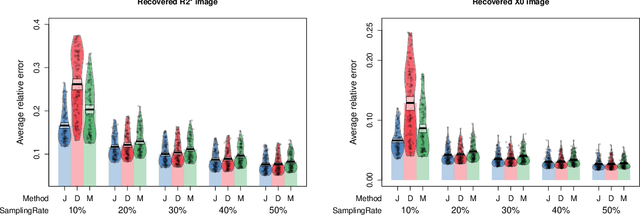
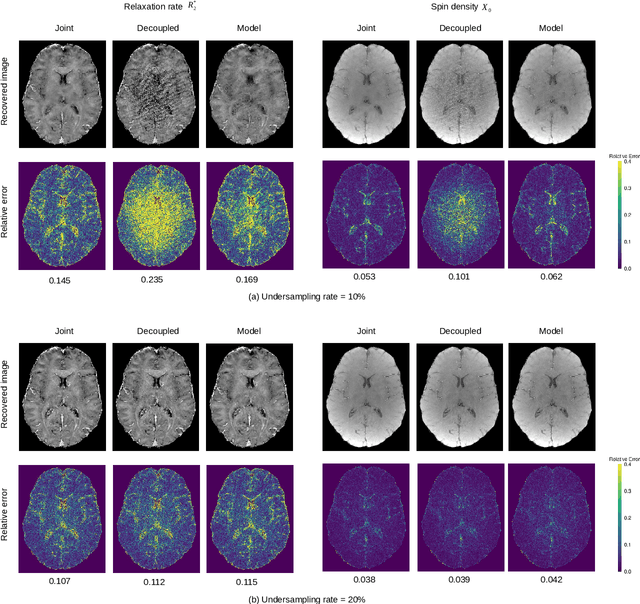
Abstract:Magnetic resonance (MR)-$T_2^*$ mapping is widely used to study hemorrhage, calcification and iron deposition in various clinical applications, it provides a direct and precise mapping of desired contrast in the tissue. However, the long acquisition time required by conventional 3D high-resolution $T_2^*$ mapping method causes discomfort to patients and introduces motion artifacts to reconstructed images, which limits its wider applicability. In this paper we address this issue by performing $T_2^*$ mapping from undersampled data using compressive sensing (CS). We formulate the reconstruction as a nonconvex problem that can be decomposed into two subproblems. They can be solved either separately via the standard approach or jointly via the alternating direction method of multipliers (ADMM). Compared to previous CS-based approaches that only apply sparse regularization on the spin density $\boldsymbol X_0$ and the relaxation rate $\boldsymbol R_2^*$, our formulation enforces additional sparse priors on the $T_2^*$-weighted images at multiple echoes to improve the reconstruction performance. We performed convergence analysis of the proposed algorithm, evaluated its performance on in vivo data, and studied the effects of different sampling schemes. Experimental results showed that the proposed joint-recovery approach generally outperforms the state-of-the-art method, especially in the low-sampling rate regime, making it a preferred choice to perform fast 3D $T_2^*$ mapping in practice. The framework adopted in this work can be easily extended to other problems arising from MR or other imaging modalities with non-linearly coupled variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge