Approximate Message Passing with Parameter Estimation for Heavily Quantized Measurements
Paper and Code
May 20, 2022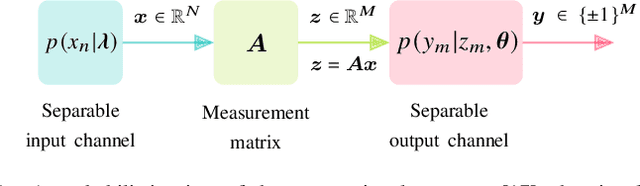
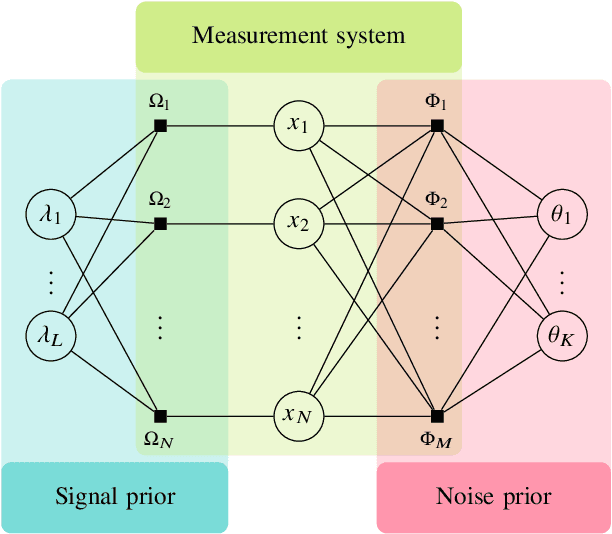
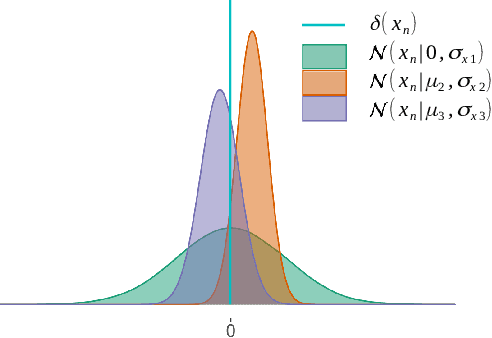
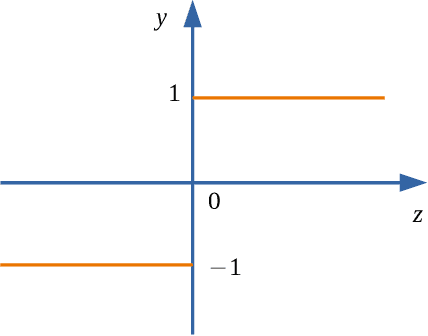
Designing efficient sparse recovery algorithms that could handle noisy quantized measurements is important in a variety of applications -- from radar to source localization, spectrum sensing and wireless networking. We take advantage of the approximate message passing (AMP) framework to achieve this goal given its high computational efficiency and state-of-the-art performance. In AMP, the signal of interest is assumed to follow certain prior distribution with unknown parameters. Previous works focused on finding the parameters that maximize the measurement likelihood via expectation maximization -- an increasingly difficult problem to solve in cases involving complicated probability models. In this paper, we treat the parameters as unknown variables and compute their posteriors via AMP. The parameters and signal of interest can then be jointly recovered. Compared to previous methods, the proposed approach leads to a simple and elegant parameter estimation scheme, allowing us to directly work with 1-bit quantization noise model. We then further extend our approach to general multi-bit quantization noise model. Experimental results show that the proposed framework provides significant improvement over state-of-the-art methods across a wide range of sparsity and noise levels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge