A Bayesian approach for $T_2^*$ Mapping and Quantitative Susceptibility Mapping

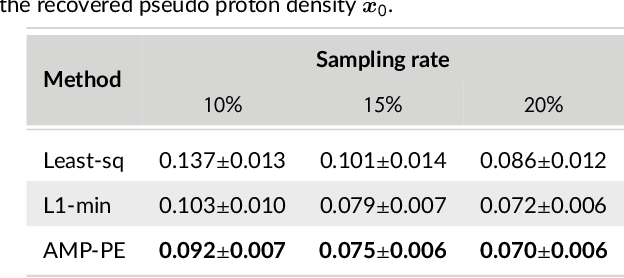
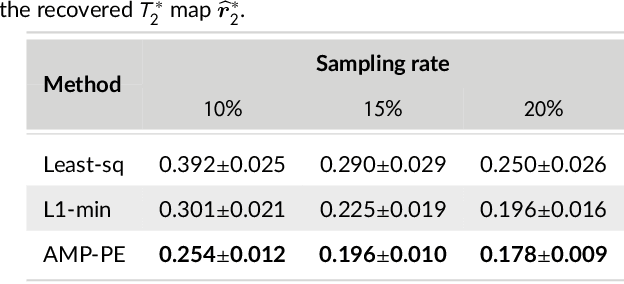
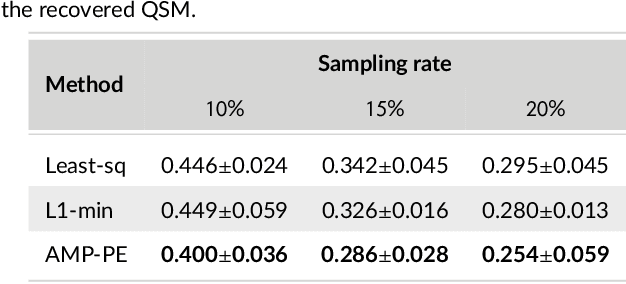
Magnetic resonance $T_2^*$ mapping and quantitative susceptibility mapping (QSM) provide direct and precise mappings of tissue contrasts. They are widely used to study iron deposition, hemorrhage and calcification in various clinical applications. In practice, the measurements can be undersampled in the $k$-space to reduce the scan time needed for high-resolution 3D maps, and sparse prior on the wavelet coefficients of images can be used to fill in the missing information via compressive sensing. To avoid the extensive parameter tuning process of conventional regularization methods, we adopt a Bayesian approach to perform $T_2^*$ mapping and QSM using approximate message passing (AMP): the sparse prior is enforced through probability distributions, and the distribution parameters can be automatically and adaptively estimated. In this paper we propose a new nonlinear AMP framework that incorporates the mono-exponential decay model, and use it to recover the proton density, the $T_2^*$ map and complex multi-echo images. The QSM can be computed from the multi-echo images subsequently. Experimental results show that the proposed approach successfully recovers $T_2^*$ map and QSM across various sampling rates, and performs much better than the state-of-the-art $l_1$-norm regularization approach.