DeepDRK: Deep Dependency Regularized Knockoff for Feature Selection

Model-X knockoff, among various feature selection methods, received much attention recently due to its guarantee on false discovery rate (FDR) control. Subsequent to its introduction in parametric design, knockoff is advanced to handle arbitrary data distributions using deep learning-based generative modeling. However, we observed that current implementations of the deep Model-X knockoff framework exhibit limitations. Notably, the "swap property" that knockoffs necessitate frequently encounter challenges on sample level, leading to a diminished selection power. To overcome, we develop "Deep Dependency Regularized Knockoff (DeepDRK)", a distribution-free deep learning method that strikes a balance between FDR and power. In DeepDRK, a generative model grounded in a transformer architecture is introduced to better achieve the "swap property". Novel efficient regularization techniques are also proposed to reach higher power. Our model outperforms other benchmarks in synthetic, semi-synthetic, and real-world data, especially when sample size is small and data distribution is complex.

Convolutional GRU Network for Seasonal Prediction of the El Niño-Southern Oscillation

Predicting sea surface temperature (SST) within the El Ni\~no-Southern Oscillation (ENSO) region has been extensively studied due to its significant influence on global temperature and precipitation patterns. Statistical models such as linear inverse model (LIM), analog forecasting (AF), and recurrent neural network (RNN) have been widely used for ENSO prediction, offering flexibility and relatively low computational expense compared to large dynamic models. However, these models have limitations in capturing spatial patterns in SST variability or relying on linear dynamics. Here we present a modified Convolutional Gated Recurrent Unit (ConvGRU) network for the ENSO region spatio-temporal sequence prediction problem, along with the Ni\~no 3.4 index prediction as a down stream task. The proposed ConvGRU network, with an encoder-decoder sequence-to-sequence structure, takes historical SST maps of the Pacific region as input and generates future SST maps for subsequent months within the ENSO region. To evaluate the performance of the ConvGRU network, we trained and tested it using data from multiple large climate models. The results demonstrate that the ConvGRU network significantly improves the predictability of the Ni\~no 3.4 index compared to LIM, AF, and RNN. This improvement is evidenced by extended useful prediction range, higher Pearson correlation, and lower root-mean-square error. The proposed model holds promise for improving our understanding and predicting capabilities of the ENSO phenomenon and can be broadly applicable to other weather and climate prediction scenarios with spatial patterns and teleconnections.

FAIR AI Models in High Energy Physics

The findable, accessible, interoperable, and reusable (FAIR) data principles have provided a framework for examining, evaluating, and improving how we share data with the aim of facilitating scientific discovery. Efforts have been made to generalize these principles to research software and other digital products. Artificial intelligence (AI) models -- algorithms that have been trained on data rather than explicitly programmed -- are an important target for this because of the ever-increasing pace with which AI is transforming scientific and engineering domains. In this paper, we propose a practical definition of FAIR principles for AI models and create a FAIR AI project template that promotes adherence to these principles. We demonstrate how to implement these principles using a concrete example from experimental high energy physics: a graph neural network for identifying Higgs bosons decaying to bottom quarks. We study the robustness of these FAIR AI models and their portability across hardware architectures and software frameworks, and report new insights on the interpretability of AI predictions by studying the interplay between FAIR datasets and AI models. Enabled by publishing FAIR AI models, these studies pave the way toward reliable and automated AI-driven scientific discovery.

Initialization and Alignment for Adversarial Texture Optimization

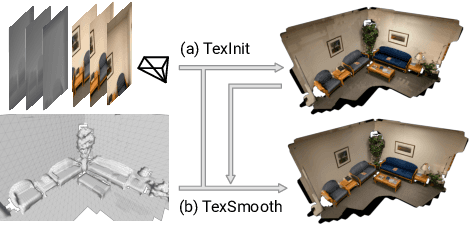
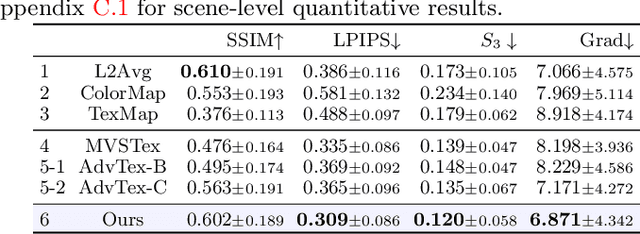
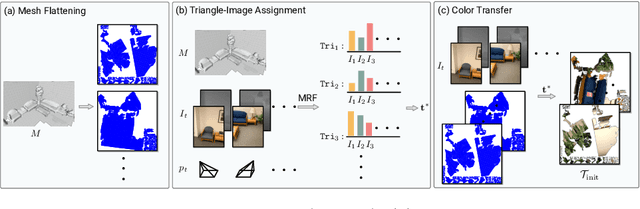
While recovery of geometry from image and video data has received a lot of attention in computer vision, methods to capture the texture for a given geometry are less mature. Specifically, classical methods for texture generation often assume clean geometry and reasonably well-aligned image data. While very recent methods, e.g., adversarial texture optimization, better handle lower-quality data obtained from hand-held devices, we find them to still struggle frequently. To improve robustness, particularly of recent adversarial texture optimization, we develop an explicit initialization and an alignment procedure. It deals with complex geometry due to a robust mapping of the geometry to the texture map and a hard-assignment-based initialization. It deals with misalignment of geometry and images by integrating fast image-alignment into the texture refinement optimization. We demonstrate efficacy of our texture generation on a dataset of 11 scenes with a total of 2807 frames, observing 7.8% and 11.1% relative improvements regarding perceptual and sharpness measurements.

Orthogonal Matrix Retrieval with Spatial Consensus for 3D Unknown-View Tomography

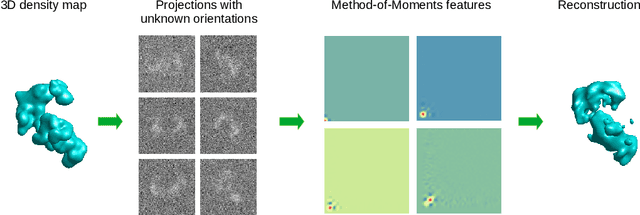
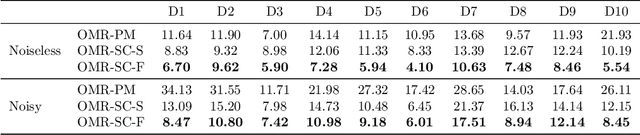
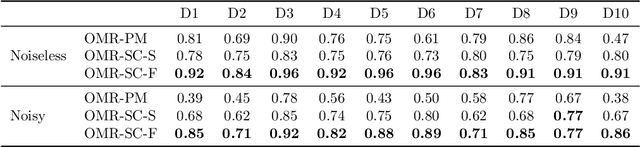
Unknown-view tomography (UVT) reconstructs a 3D density map from its 2D projections at unknown, random orientations. A line of work starting with Kam (1980) employs the method of moments (MoM) with rotation-invariant Fourier features to solve UVT in the frequency domain, assuming that the orientations are uniformly distributed. This line of work includes the recent orthogonal matrix retrieval (OMR) approaches based on matrix factorization, which, while elegant, either require side information about the density that is not available, or fail to be sufficiently robust. In order for OMR to break free from those restrictions, we propose to jointly recover the density map and the orthogonal matrices by requiring that they be mutually consistent. We regularize the resulting non-convex optimization problem by a denoised reference projection and a nonnegativity constraint. This is enabled by the new closed-form expressions for spatial autocorrelation features. Further, we design an easy-to-compute initial density map which effectively mitigates the non-convexity of the reconstruction problem. Experimental results show that the proposed OMR with spatial consensus is more robust and performs significantly better than the previous state-of-the-art OMR approach in the typical low-SNR scenario of 3D UVT.

Multi-Frequency Joint Community Detection and Phase Synchronization

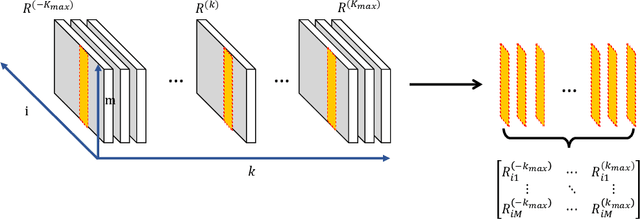
This paper studies the joint community detection and phase synchronization problem on the \textit{stochastic block model with relative phase}, where each node is associated with a phase. This problem, with a variety of real-world applications, aims to recover community memberships and associated phases simultaneously. By studying the maximum likelihood estimation formulation, we show that this problem exhibits a \textit{``multi-frequency''} structure. To this end, two simple yet efficient algorithms that leverage information across multiple frequencies are proposed. The former is a spectral method based on the novel multi-frequency column-pivoted QR factorization, and the latter is an iterative multi-frequency generalized power method. Numerical experiments indicate our proposed algorithms outperform state-of-the-art algorithms, in recovering community memberships and associated phases.

A Spectral Method for Joint Community Detection and Orthogonal Group Synchronization

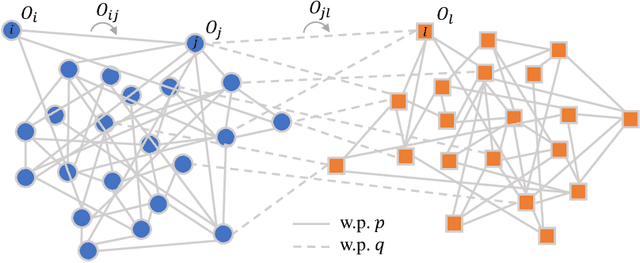
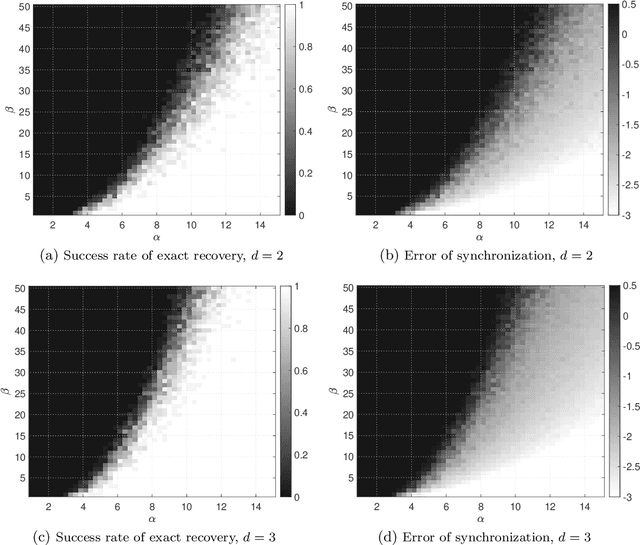
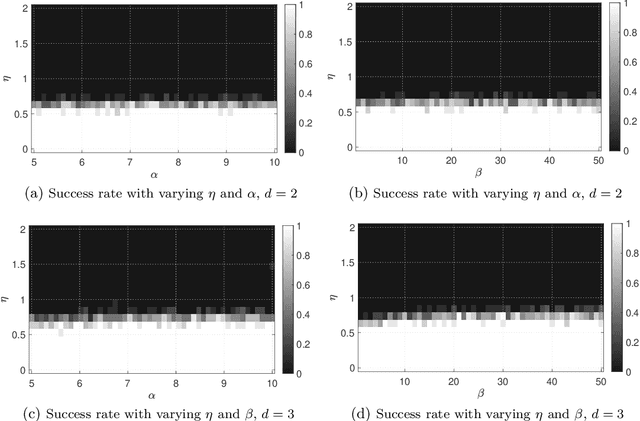
Community detection and orthogonal group synchronization are both fundamental problems with a variety of important applications in science and engineering. In this work, we consider the joint problem of community detection and orthogonal group synchronization which aims to recover the communities and perform synchronization simultaneously. To this end, we propose a simple algorithm that consists of a spectral decomposition step followed by a blockwise column pivoted QR factorization (CPQR). The proposed algorithm is efficient and scales linearly with the number of data points. We also leverage the recently developed `leave-one-out' technique to establish a near-optimal guarantee for exact recovery of the cluster memberships and stable recovery of the orthogonal transforms. Numerical experiments demonstrate the efficiency and efficacy of our algorithm and confirm our theoretical characterization of it.

An Adversarial Learning Based Approach for Unknown View Tomographic Reconstruction

The goal of 2D tomographic reconstruction is to recover an image given its projection lines from various views. It is often presumed that projection angles associated with the projection lines are known in advance. Under certain situations, however, these angles are known only approximately or are completely unknown. It becomes more challenging to reconstruct the image from a collection of random projection lines. We propose an adversarial learning based approach to recover the image and the projection angle distribution by matching the empirical distribution of the measurements with the generated data. Fitting the distributions is achieved through solving a min-max game between a generator and a critic based on Wasserstein generative adversarial network structure. To accommodate the update of the projection angle distribution through gradient back propagation, we approximate the loss using the Gumbel-Softmax reparameterization of samples from discrete distributions. Our theoretical analysis verifies the unique recovery of the image and the projection distribution up to a rotation and reflection upon convergence. Our extensive numerical experiments showcase the potential of our method to accurately recover the image and the projection angle distribution under noise contamination.

A FAIR and AI-ready Higgs Boson Decay Dataset

To enable the reusability of massive scientific datasets by humans and machines, researchers aim to create scientific datasets that adhere to the principles of findability, accessibility, interoperability, and reusability (FAIR) for data and artificial intelligence (AI) models. This article provides a domain-agnostic, step-by-step assessment guide to evaluate whether or not a given dataset meets each FAIR principle. We then demonstrate how to use this guide to evaluate the FAIRness of an open simulated dataset produced by the CMS Collaboration at the CERN Large Hadron Collider. This dataset consists of Higgs boson decays and quark and gluon background, and is available through the CERN Open Data Portal. We also use other available tools to assess the FAIRness of this dataset, and incorporate feedback from members of the FAIR community to validate our results. This article is accompanied by a Jupyter notebook to facilitate an understanding and exploration of the dataset, including visualization of its elements. This study marks the first in a planned series of articles that will guide scientists in the creation and quantification of FAIRness in high energy particle physics datasets and AI models.

Spacetime Neural Network for High Dimensional Quantum Dynamics

We develop a spacetime neural network method with second order optimization for solving quantum dynamics from the high dimensional Schr\"{o}dinger equation. In contrast to the standard iterative first order optimization and the time-dependent variational principle, our approach utilizes the implicit mid-point method and generates the solution for all spatial and temporal values simultaneously after optimization. We demonstrate the method in the Schr\"{o}dinger equation with a self-normalized autoregressive spacetime neural network construction. Future explorations for solving different high dimensional differential equations are discussed.