Lingda Wang
Convolutional GRU Network for Seasonal Prediction of the El Niño-Southern Oscillation
Jun 18, 2023Abstract:Predicting sea surface temperature (SST) within the El Ni\~no-Southern Oscillation (ENSO) region has been extensively studied due to its significant influence on global temperature and precipitation patterns. Statistical models such as linear inverse model (LIM), analog forecasting (AF), and recurrent neural network (RNN) have been widely used for ENSO prediction, offering flexibility and relatively low computational expense compared to large dynamic models. However, these models have limitations in capturing spatial patterns in SST variability or relying on linear dynamics. Here we present a modified Convolutional Gated Recurrent Unit (ConvGRU) network for the ENSO region spatio-temporal sequence prediction problem, along with the Ni\~no 3.4 index prediction as a down stream task. The proposed ConvGRU network, with an encoder-decoder sequence-to-sequence structure, takes historical SST maps of the Pacific region as input and generates future SST maps for subsequent months within the ENSO region. To evaluate the performance of the ConvGRU network, we trained and tested it using data from multiple large climate models. The results demonstrate that the ConvGRU network significantly improves the predictability of the Ni\~no 3.4 index compared to LIM, AF, and RNN. This improvement is evidenced by extended useful prediction range, higher Pearson correlation, and lower root-mean-square error. The proposed model holds promise for improving our understanding and predicting capabilities of the ENSO phenomenon and can be broadly applicable to other weather and climate prediction scenarios with spatial patterns and teleconnections.
Multi-Frequency Joint Community Detection and Phase Synchronization
Jun 16, 2022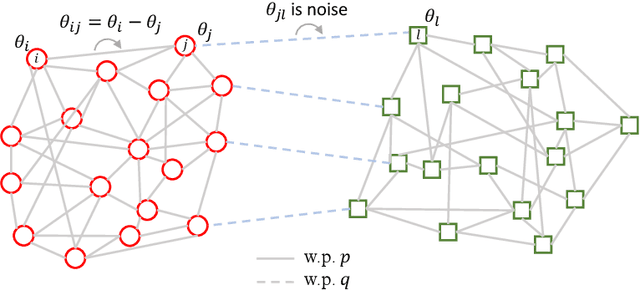


Abstract:This paper studies the joint community detection and phase synchronization problem on the \textit{stochastic block model with relative phase}, where each node is associated with a phase. This problem, with a variety of real-world applications, aims to recover community memberships and associated phases simultaneously. By studying the maximum likelihood estimation formulation, we show that this problem exhibits a \textit{``multi-frequency''} structure. To this end, two simple yet efficient algorithms that leverage information across multiple frequencies are proposed. The former is a spectral method based on the novel multi-frequency column-pivoted QR factorization, and the latter is an iterative multi-frequency generalized power method. Numerical experiments indicate our proposed algorithms outperform state-of-the-art algorithms, in recovering community memberships and associated phases.
Robust Nonparametric Distribution Forecast with Backtest-based Bootstrap and Adaptive Residual Selection
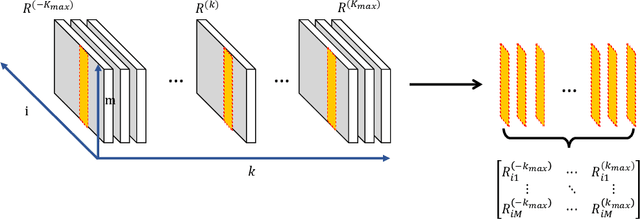
Feb 16, 2022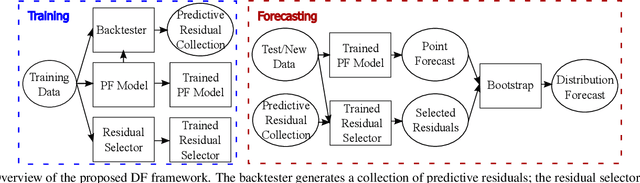
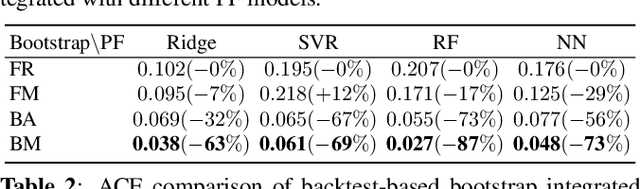
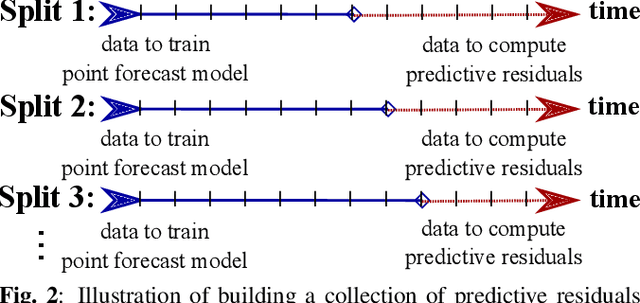

Abstract:Distribution forecast can quantify forecast uncertainty and provide various forecast scenarios with their corresponding estimated probabilities. Accurate distribution forecast is crucial for planning - for example when making production capacity or inventory allocation decisions. We propose a practical and robust distribution forecast framework that relies on backtest-based bootstrap and adaptive residual selection. The proposed approach is robust to the choice of the underlying forecasting model, accounts for uncertainty around the input covariates, and relaxes the independence between residuals and covariates assumption. It reduces the Absolute Coverage Error by more than 63% compared to the classic bootstrap approaches and by 2% - 32% compared to a variety of State-of-the-Art deep learning approaches on in-house product sales data and M4-hourly competition data.
Adversarial Linear Contextual Bandits with Graph-Structured Side Observations
Dec 28, 2020

Abstract:This paper studies the adversarial graphical contextual bandits, a variant of adversarial multi-armed bandits that leverage two categories of the most common side information: \emph{contexts} and \emph{side observations}. In this setting, a learning agent repeatedly chooses from a set of $K$ actions after being presented with a $d$-dimensional context vector. The agent not only incurs and observes the loss of the chosen action, but also observes the losses of its neighboring actions in the observation structures, which are encoded as a series of feedback graphs. This setting models a variety of applications in social networks, where both contexts and graph-structured side observations are available. Two efficient algorithms are developed based on \texttt{EXP3}. Under mild conditions, our analysis shows that for undirected feedback graphs the first algorithm, \texttt{EXP3-LGC-U}, achieves the regret of order $\mathcal{O}(\sqrt{(K+\alpha(G)d)T\log{K}})$ over the time horizon $T$, where $\alpha(G)$ is the average \emph{independence number} of the feedback graphs. A slightly weaker result is presented for the directed graph setting as well. The second algorithm, \texttt{EXP3-LGC-IX}, is developed for a special class of problems, for which the regret is reduced to $\mathcal{O}(\sqrt{\alpha(G)dT\log{K}\log(KT)})$ for both directed as well as undirected feedback graphs. Numerical tests corroborate the efficiency of proposed algorithms.
Enhancing Parameter-Free Frank Wolfe with an Extra Subproblem
Dec 09, 2020



Abstract:Aiming at convex optimization under structural constraints, this work introduces and analyzes a variant of the Frank Wolfe (FW) algorithm termed ExtraFW. The distinct feature of ExtraFW is the pair of gradients leveraged per iteration, thanks to which the decision variable is updated in a prediction-correction (PC) format. Relying on no problem dependent parameters in the step sizes, the convergence rate of ExtraFW for general convex problems is shown to be ${\cal O}(\frac{1}{k})$, which is optimal in the sense of matching the lower bound on the number of solved FW subproblems. However, the merit of ExtraFW is its faster rate ${\cal O}\big(\frac{1}{k^2} \big)$ on a class of machine learning problems. Compared with other parameter-free FW variants that have faster rates on the same problems, ExtraFW has improved rates and fine-grained analysis thanks to its PC update. Numerical tests on binary classification with different sparsity-promoting constraints demonstrate that the empirical performance of ExtraFW is significantly better than FW, and even faster than Nesterov's accelerated gradient on certain datasets. For matrix completion, ExtraFW enjoys smaller optimality gap, and lower rank than FW.
Be Aware of Non-Stationarity: Nearly Optimal Algorithms for Piecewise-Stationary Cascading Bandits
Oct 07, 2019



Abstract:Cascading bandit (CB) is a variant of both the multi-armed bandit (MAB) and the cascade model (CM), where a learning agent aims to maximize the total reward by recommending $K$ out of $L$ items to a user. We focus on a common real-world scenario where the user's preference can change in a piecewise-stationary manner. Two efficient algorithms, \texttt{GLRT-CascadeUCB} and \texttt{GLRT-CascadeKL-UCB}, are developed. The key idea behind the proposed algorithms is incorporating an almost parameter-free change-point detector, the Generalized Likelihood Ratio Test (GLRT), within classical upper confidence bound (UCB) based algorithms. Gap-dependent regret upper bounds of the proposed algorithms are derived, both on the order of $\mathcal{O}(\sqrt{NLT\log{T}})$, where $N$ is the number of piecewise-stationary segments, and $T$ is the time horizon. We also derive a minimax lower bound on the order of $\mathcal{O}(\sqrt{NLT})$ for piecewise-stationary CB, showing that our proposed algorithms are optimal up to a poly-logarithmic factor $\sqrt{\log T}$. Lastly, we present numerical experiments on both synthetic and real-world datasets to show that \texttt{GLRT-CascadeUCB} and \texttt{GLRT-CascadeKL-UCB} outperform state-of-the-art algorithms in the literature.
A Near-Optimal Change-Detection Based Algorithm for Piecewise-Stationary Combinatorial Semi-Bandits
Aug 29, 2019



Abstract:We investigate the piecewise-stationary combinatorial semi-bandit problem. Compared to the original combinatorial semi-bandit problem, our setting assumes the reward distributions of base arms may change in a piecewise-stationary manner at unknown time steps. We propose an algorithm, \texttt{GLR-CUCB}, which incorporates an efficient combinatorial semi-bandit algorithm, \texttt{CUCB}, with an almost parameter-free change-point detector, the \emph{Generalized Likelihood Ratio Test} (GLRT). Our analysis shows that the regret of \texttt{GLR-CUCB} is upper bounded by $\mathcal{O}(\sqrt{NKT\log{T}})$, where $N$ is the number of piecewise-stationary segments, $K$ is the number of base arms, and $T$ is the number of time steps. As a complement, we also derive a nearly matching regret lower bound on the order of $\Omega(\sqrt{NKT}$), for both piecewise-stationary multi-armed bandits and combinatorial semi-bandits, using information-theoretic techniques and judiciously constructed piecewise-stationary bandit instances. Our lower bound is tighter than the best available regret lower bound, which is $\Omega(\sqrt{T})$. Numerical experiments on both synthetic and real-world datasets demonstrate the superiority of \texttt{GLR-CUCB} compared to other state-of-the-art algorithms.
Almost Tune-Free Variance Reduction
Aug 25, 2019



Abstract:The variance reduction class of algorithms including the representative ones, abbreviated as SVRG and SARAH, have well documented merits for empirical risk minimization tasks. However, they require grid search to optimally tune parameters (step size and the number of iterations per inner loop) for best performance. This work introduces `almost tune-free' SVRG and SARAH schemes by equipping them with Barzilai-Borwein (BB) step sizes. To achieve the best performance, both i) averaging schemes; and, ii) the inner loop length are adjusted according to the BB step size. SVRG and SARAH are first reexamined through an `estimate sequence' lens. Such analysis provides new averaging methods that tighten the convergence rates of both SVRG and SARAH theoretically, and improve their performance empirically when the step size is chosen large. Then a simple yet effective means of adjusting the number of iterations per inner loop is developed, which completes the tune-free variance reduction together with BB step sizes. Numerical tests corroborate the proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge