Convolutional GRU Network for Seasonal Prediction of the El Niño-Southern Oscillation

Predicting sea surface temperature (SST) within the El Ni\~no-Southern Oscillation (ENSO) region has been extensively studied due to its significant influence on global temperature and precipitation patterns. Statistical models such as linear inverse model (LIM), analog forecasting (AF), and recurrent neural network (RNN) have been widely used for ENSO prediction, offering flexibility and relatively low computational expense compared to large dynamic models. However, these models have limitations in capturing spatial patterns in SST variability or relying on linear dynamics. Here we present a modified Convolutional Gated Recurrent Unit (ConvGRU) network for the ENSO region spatio-temporal sequence prediction problem, along with the Ni\~no 3.4 index prediction as a down stream task. The proposed ConvGRU network, with an encoder-decoder sequence-to-sequence structure, takes historical SST maps of the Pacific region as input and generates future SST maps for subsequent months within the ENSO region. To evaluate the performance of the ConvGRU network, we trained and tested it using data from multiple large climate models. The results demonstrate that the ConvGRU network significantly improves the predictability of the Ni\~no 3.4 index compared to LIM, AF, and RNN. This improvement is evidenced by extended useful prediction range, higher Pearson correlation, and lower root-mean-square error. The proposed model holds promise for improving our understanding and predicting capabilities of the ENSO phenomenon and can be broadly applicable to other weather and climate prediction scenarios with spatial patterns and teleconnections.

Spacetime Neural Network for High Dimensional Quantum Dynamics

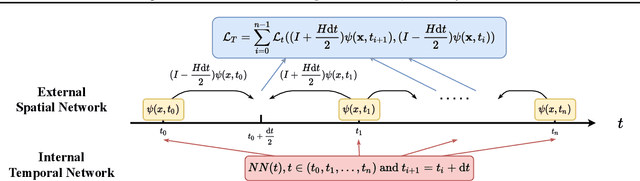
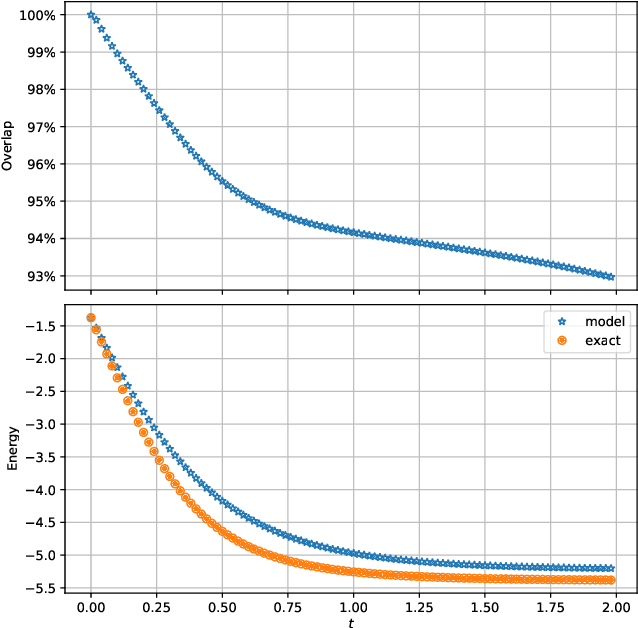
We develop a spacetime neural network method with second order optimization for solving quantum dynamics from the high dimensional Schr\"{o}dinger equation. In contrast to the standard iterative first order optimization and the time-dependent variational principle, our approach utilizes the implicit mid-point method and generates the solution for all spatial and temporal values simultaneously after optimization. We demonstrate the method in the Schr\"{o}dinger equation with a self-normalized autoregressive spacetime neural network construction. Future explorations for solving different high dimensional differential equations are discussed.

Gauge Invariant Autoregressive Neural Networks for Quantum Lattice Models

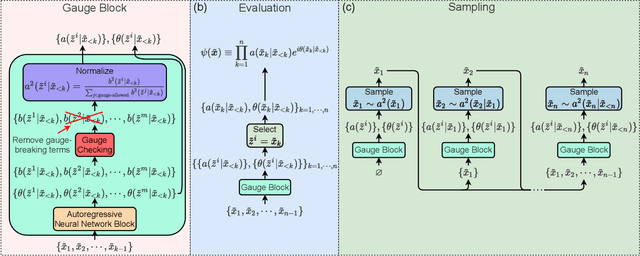
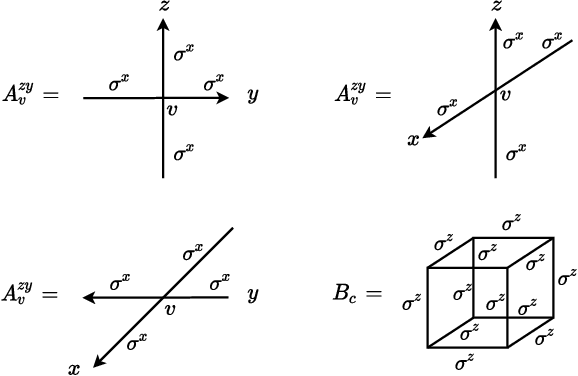
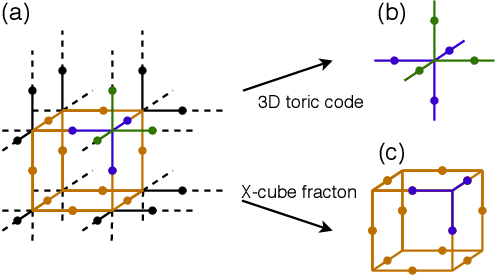
Gauge invariance plays a crucial role in quantum mechanics from condensed matter physics to high energy physics. We develop an approach to constructing gauge invariant autoregressive neural networks for quantum lattice models. These networks can be efficiently sampled and explicitly obey gauge symmetries. We variationally optimize our gauge invariant autoregressive neural networks for ground states as well as real-time dynamics for a variety of models. We exactly represent the ground and excited states of the 2D and 3D toric codes, and the X-cube fracton model. We simulate the dynamics of the quantum link model of $\text{U(1)}$ lattice gauge theory, obtain the phase diagram for the 2D $\mathbb{Z}_2$ gauge theory, determine the phase transition and the central charge of the $\text{SU(2)}_3$ anyonic chain, and also compute the ground state energy of the $\text{SU(2)}$ invariant Heisenberg spin chain. Our approach provides powerful tools for exploring condensed matter physics, high energy physics and quantum information science.