Understanding the Role of Equivariance in Self-supervised Learning

Contrastive learning has been a leading paradigm for self-supervised learning, but it is widely observed that it comes at the price of sacrificing useful features (\eg colors) by being invariant to data augmentations. Given this limitation, there has been a surge of interest in equivariant self-supervised learning (E-SSL) that learns features to be augmentation-aware. However, even for the simplest rotation prediction method, there is a lack of rigorous understanding of why, when, and how E-SSL learns useful features for downstream tasks. To bridge this gap between practice and theory, we establish an information-theoretic perspective to understand the generalization ability of E-SSL. In particular, we identify a critical explaining-away effect in E-SSL that creates a synergy between the equivariant and classification tasks. This synergy effect encourages models to extract class-relevant features to improve its equivariant prediction, which, in turn, benefits downstream tasks requiring semantic features. Based on this perspective, we theoretically analyze the influence of data transformations and reveal several principles for practical designs of E-SSL. Our theory not only aligns well with existing E-SSL methods but also sheds light on new directions by exploring the benefits of model equivariance. We believe that a theoretically grounded understanding on the role of equivariance would inspire more principled and advanced designs in this field. Code is available at https://github.com/kaotty/Understanding-ESSL.

Model Doctor for Diagnosing and Treating Segmentation Error

Despite the remarkable progress in semantic segmentation tasks with the advancement of deep neural networks, existing U-shaped hierarchical typical segmentation networks still suffer from local misclassification of categories and inaccurate target boundaries. In an effort to alleviate this issue, we propose a Model Doctor for semantic segmentation problems. The Model Doctor is designed to diagnose the aforementioned problems in existing pre-trained models and treat them without introducing additional data, with the goal of refining the parameters to achieve better performance. Extensive experiments on several benchmark datasets demonstrate the effectiveness of our method. Code is available at \url{https://github.com/zhijiejia/SegDoctor}.

Simulating 2+1D Lattice Quantum Electrodynamics at Finite Density with Neural Flow Wavefunctions

We present a neural flow wavefunction, Gauge-Fermion FlowNet, and use it to simulate 2+1D lattice compact quantum electrodynamics with finite density dynamical fermions. The gauge field is represented by a neural network which parameterizes a discretized flow-based transformation of the amplitude while the fermionic sign structure is represented by a neural net backflow. This approach directly represents the $U(1)$ degree of freedom without any truncation, obeys Guass's law by construction, samples autoregressively avoiding any equilibration time, and variationally simulates Gauge-Fermion systems with sign problems accurately. In this model, we investigate confinement and string breaking phenomena in different fermion density and hopping regimes. We study the phase transition from the charge crystal phase to the vacuum phase at zero density, and observe the phase seperation and the net charge penetration blocking effect under magnetic interaction at finite density. In addition, we investigate a magnetic phase transition due to the competition effect between the kinetic energy of fermions and the magnetic energy of the gauge field. With our method, we further note potential differences on the order of the phase transitions between a continuous $U(1)$ system and one with finite truncation. Our state-of-the-art neural network approach opens up new possibilities to study different gauge theories coupled to dynamical matter in higher dimensions.

Gauge Invariant Autoregressive Neural Networks for Quantum Lattice Models

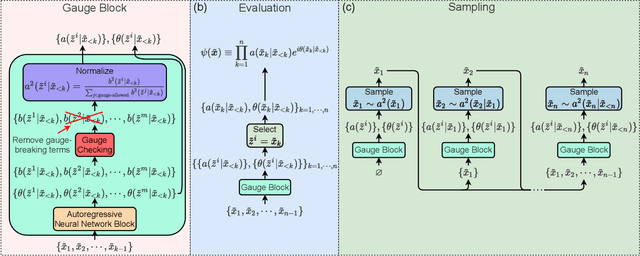
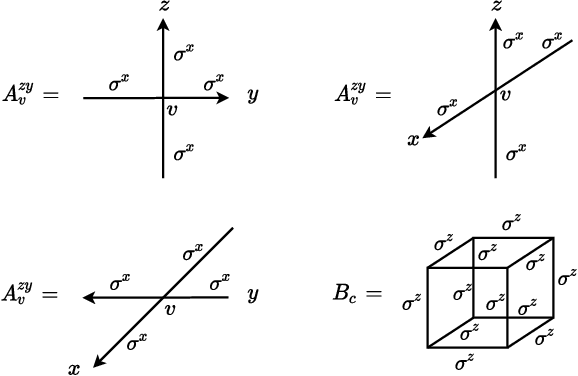
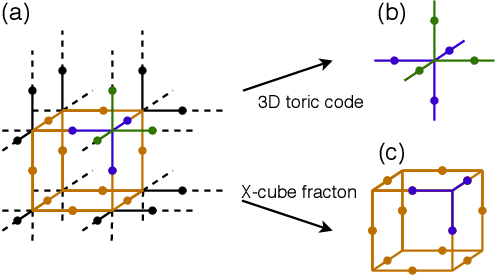
Gauge invariance plays a crucial role in quantum mechanics from condensed matter physics to high energy physics. We develop an approach to constructing gauge invariant autoregressive neural networks for quantum lattice models. These networks can be efficiently sampled and explicitly obey gauge symmetries. We variationally optimize our gauge invariant autoregressive neural networks for ground states as well as real-time dynamics for a variety of models. We exactly represent the ground and excited states of the 2D and 3D toric codes, and the X-cube fracton model. We simulate the dynamics of the quantum link model of $\text{U(1)}$ lattice gauge theory, obtain the phase diagram for the 2D $\mathbb{Z}_2$ gauge theory, determine the phase transition and the central charge of the $\text{SU(2)}_3$ anyonic chain, and also compute the ground state energy of the $\text{SU(2)}$ invariant Heisenberg spin chain. Our approach provides powerful tools for exploring condensed matter physics, high energy physics and quantum information science.