Transforming the Hybrid Cloud for Emerging AI Workloads

This white paper, developed through close collaboration between IBM Research and UIUC researchers within the IIDAI Institute, envisions transforming hybrid cloud systems to meet the growing complexity of AI workloads through innovative, full-stack co-design approaches, emphasizing usability, manageability, affordability, adaptability, efficiency, and scalability. By integrating cutting-edge technologies such as generative and agentic AI, cross-layer automation and optimization, unified control plane, and composable and adaptive system architecture, the proposed framework addresses critical challenges in energy efficiency, performance, and cost-effectiveness. Incorporating quantum computing as it matures will enable quantum-accelerated simulations for materials science, climate modeling, and other high-impact domains. Collaborative efforts between academia and industry are central to this vision, driving advancements in foundation models for material design and climate solutions, scalable multimodal data processing, and enhanced physics-based AI emulators for applications like weather forecasting and carbon sequestration. Research priorities include advancing AI agentic systems, LLM as an Abstraction (LLMaaA), AI model optimization and unified abstractions across heterogeneous infrastructure, end-to-end edge-cloud transformation, efficient programming model, middleware and platform, secure infrastructure, application-adaptive cloud systems, and new quantum-classical collaborative workflows. These ideas and solutions encompass both theoretical and practical research questions, requiring coordinated input and support from the research community. This joint initiative aims to establish hybrid clouds as secure, efficient, and sustainable platforms, fostering breakthroughs in AI-driven applications and scientific discovery across academia, industry, and society.

Using CycleGANs to Generate Realistic STEM Images for Machine Learning

The rise of automation and machine learning (ML) in electron microscopy has the potential to revolutionize materials research by enabling the autonomous collection and processing of vast amounts of atomic resolution data. However, a major challenge is developing ML models that can reliably and rapidly generalize to large data sets with varying experimental conditions. To overcome this challenge, we develop a cycle generative adversarial network (CycleGAN) that introduces a novel reciprocal space discriminator to augment simulated data with realistic, complex spatial frequency information learned from experimental data. This enables the CycleGAN to generate nearly indistinguishable images from real experimental data, while also providing labels for further ML applications. We demonstrate the effectiveness of this approach by training a fully convolutional network (FCN) to identify single atom defects in a large data set of 4.5 million atoms, which we collected using automated acquisition in an aberration-corrected scanning transmission electron microscope (STEM). Our approach yields highly adaptable FCNs that can adjust to dynamically changing experimental variables, such as lens aberrations, noise, and local contamination, with minimal manual intervention. This represents a significant step towards building fully autonomous approaches for harnessing microscopy big data.

Simulating 2+1D Lattice Quantum Electrodynamics at Finite Density with Neural Flow Wavefunctions

We present a neural flow wavefunction, Gauge-Fermion FlowNet, and use it to simulate 2+1D lattice compact quantum electrodynamics with finite density dynamical fermions. The gauge field is represented by a neural network which parameterizes a discretized flow-based transformation of the amplitude while the fermionic sign structure is represented by a neural net backflow. This approach directly represents the $U(1)$ degree of freedom without any truncation, obeys Guass's law by construction, samples autoregressively avoiding any equilibration time, and variationally simulates Gauge-Fermion systems with sign problems accurately. In this model, we investigate confinement and string breaking phenomena in different fermion density and hopping regimes. We study the phase transition from the charge crystal phase to the vacuum phase at zero density, and observe the phase seperation and the net charge penetration blocking effect under magnetic interaction at finite density. In addition, we investigate a magnetic phase transition due to the competition effect between the kinetic energy of fermions and the magnetic energy of the gauge field. With our method, we further note potential differences on the order of the phase transitions between a continuous $U(1)$ system and one with finite truncation. Our state-of-the-art neural network approach opens up new possibilities to study different gauge theories coupled to dynamical matter in higher dimensions.

Gauge Equivariant Neural Networks for 2+1D U Gauge Theory Simulations in Hamiltonian Formulation

Gauge Theory plays a crucial role in many areas in science, including high energy physics, condensed matter physics and quantum information science. In quantum simulations of lattice gauge theory, an important step is to construct a wave function that obeys gauge symmetry. In this paper, we have developed gauge equivariant neural network wave function techniques for simulating continuous-variable quantum lattice gauge theories in the Hamiltonian formulation. We have applied the gauge equivariant neural network approach to find the ground state of 2+1-dimensional lattice gauge theory with U(1) gauge group using variational Monte Carlo. We have benchmarked our approach against the state-of-the-art complex Gaussian wave functions, demonstrating improved performance in the strong coupling regime and comparable results in the weak coupling regime.

Learning ground states of quantum Hamiltonians with graph networks

Solving for the lowest energy eigenstate of the many-body Schrodinger equation is a cornerstone problem that hinders understanding of a variety of quantum phenomena. The difficulty arises from the exponential nature of the Hilbert space which casts the governing equations as an eigenvalue problem of exponentially large, structured matrices. Variational methods approach this problem by searching for the best approximation within a lower-dimensional variational manifold. In this work we use graph neural networks to define a structured variational manifold and optimize its parameters to find high quality approximations of the lowest energy solutions on a diverse set of Heisenberg Hamiltonians. Using graph networks we learn distributed representations that by construction respect underlying physical symmetries of the problem and generalize to problems of larger size. Our approach achieves state-of-the-art results on a set of quantum many-body benchmark problems and works well on problems whose solutions are not positive-definite. The discussed techniques hold promise of being a useful tool for studying quantum many-body systems and providing insights into optimization and implicit modeling of exponentially-sized objects.

Spacetime Neural Network for High Dimensional Quantum Dynamics

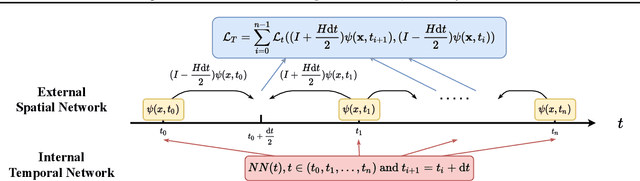
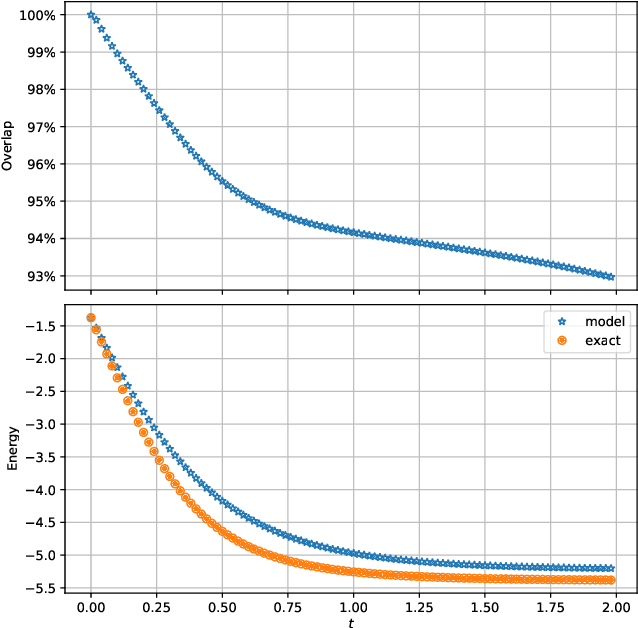
We develop a spacetime neural network method with second order optimization for solving quantum dynamics from the high dimensional Schr\"{o}dinger equation. In contrast to the standard iterative first order optimization and the time-dependent variational principle, our approach utilizes the implicit mid-point method and generates the solution for all spatial and temporal values simultaneously after optimization. We demonstrate the method in the Schr\"{o}dinger equation with a self-normalized autoregressive spacetime neural network construction. Future explorations for solving different high dimensional differential equations are discussed.

Gauge Invariant Autoregressive Neural Networks for Quantum Lattice Models

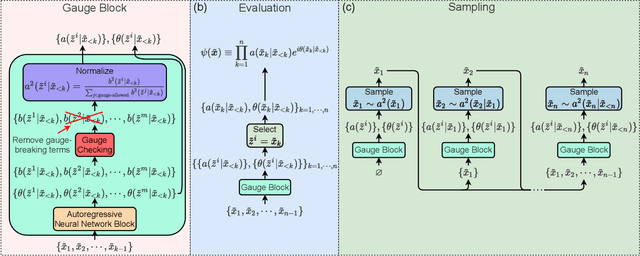
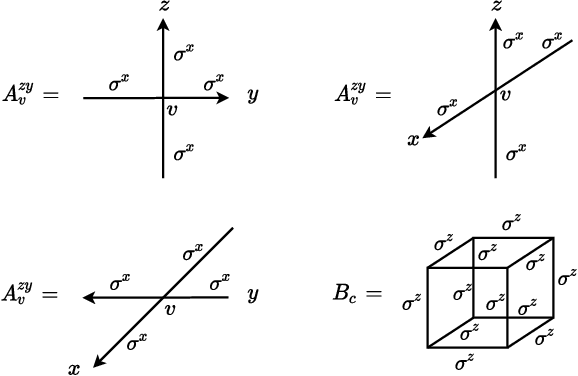
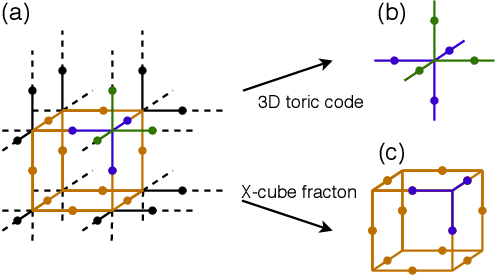
Gauge invariance plays a crucial role in quantum mechanics from condensed matter physics to high energy physics. We develop an approach to constructing gauge invariant autoregressive neural networks for quantum lattice models. These networks can be efficiently sampled and explicitly obey gauge symmetries. We variationally optimize our gauge invariant autoregressive neural networks for ground states as well as real-time dynamics for a variety of models. We exactly represent the ground and excited states of the 2D and 3D toric codes, and the X-cube fracton model. We simulate the dynamics of the quantum link model of $\text{U(1)}$ lattice gauge theory, obtain the phase diagram for the 2D $\mathbb{Z}_2$ gauge theory, determine the phase transition and the central charge of the $\text{SU(2)}_3$ anyonic chain, and also compute the ground state energy of the $\text{SU(2)}$ invariant Heisenberg spin chain. Our approach provides powerful tools for exploring condensed matter physics, high energy physics and quantum information science.

Gauge equivariant neural networks for quantum lattice gauge theories

Gauge symmetries play a key role in physics appearing in areas such as quantum field theories of the fundamental particles and emergent degrees of freedom in quantum materials. Motivated by the desire to efficiently simulate many-body quantum systems with exact local gauge invariance, gauge equivariant neural-network quantum states are introduced, which exactly satisfy the local Hilbert space constraints necessary for the description of quantum lattice gauge theory with Zd gauge group on different geometries. Focusing on the special case of Z2 gauge group on a periodically identified square lattice, the equivariant architecture is analytically shown to contain the loop-gas solution as a special case. Gauge equivariant neural-network quantum states are used in combination with variational quantum Monte Carlo to obtain compact descriptions of the ground state wavefunction for the Z2 theory away from the exactly solvable limit, and to demonstrate the confining/deconfining phase transition of the Wilson loop order parameter.