Adversarial Linear Contextual Bandits with Graph-Structured Side Observations

This paper studies the adversarial graphical contextual bandits, a variant of adversarial multi-armed bandits that leverage two categories of the most common side information: \emph{contexts} and \emph{side observations}. In this setting, a learning agent repeatedly chooses from a set of $K$ actions after being presented with a $d$-dimensional context vector. The agent not only incurs and observes the loss of the chosen action, but also observes the losses of its neighboring actions in the observation structures, which are encoded as a series of feedback graphs. This setting models a variety of applications in social networks, where both contexts and graph-structured side observations are available. Two efficient algorithms are developed based on \texttt{EXP3}. Under mild conditions, our analysis shows that for undirected feedback graphs the first algorithm, \texttt{EXP3-LGC-U}, achieves the regret of order $\mathcal{O}(\sqrt{(K+\alpha(G)d)T\log{K}})$ over the time horizon $T$, where $\alpha(G)$ is the average \emph{independence number} of the feedback graphs. A slightly weaker result is presented for the directed graph setting as well. The second algorithm, \texttt{EXP3-LGC-IX}, is developed for a special class of problems, for which the regret is reduced to $\mathcal{O}(\sqrt{\alpha(G)dT\log{K}\log(KT)})$ for both directed as well as undirected feedback graphs. Numerical tests corroborate the efficiency of proposed algorithms.

Nonstationary Reinforcement Learning with Linear Function Approximation

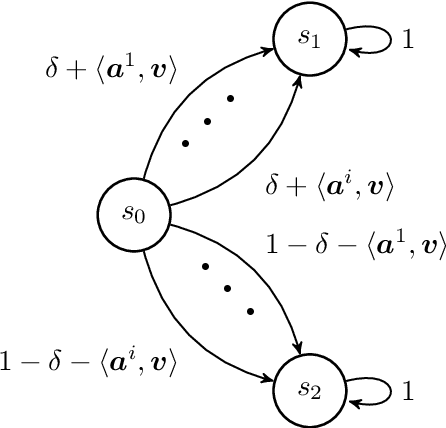
We consider reinforcement learning (RL) in episodic Markov decision processes (MDPs) with linear function approximation under drifting environment. Specifically, both the reward and state transition functions can evolve over time, as long as their respective total variations, quantified by suitable metrics, do not exceed certain \textit{variation budgets}. We first develop the $\texttt{LSVI-UCB-Restart}$ algorithm, an optimistic modification of least-squares value iteration combined with periodic restart, and establish its dynamic regret bound when variation budgets are known. We then propose a parameter-free algorithm, $\texttt{Ada-LSVI-UCB-Restart}$, that works without knowing the variation budgets, but with a slightly worse dynamic regret bound. We also derive the first minimax dynamic regret lower bound for nonstationary MDPs to show that our proposed algorithms are near-optimal. As a byproduct, we establish a minimax regret lower bound for linear MDPs, which is unsolved by \cite{jin2020provably}. In addition, we provide numerical experiments to demonstrate the effectiveness of our proposed algorithms. As far as we know, this is the first dynamic regret analysis in nonstationary reinforcement learning with function approximation.

Be Aware of Non-Stationarity: Nearly Optimal Algorithms for Piecewise-Stationary Cascading Bandits

Cascading bandit (CB) is a variant of both the multi-armed bandit (MAB) and the cascade model (CM), where a learning agent aims to maximize the total reward by recommending $K$ out of $L$ items to a user. We focus on a common real-world scenario where the user's preference can change in a piecewise-stationary manner. Two efficient algorithms, \texttt{GLRT-CascadeUCB} and \texttt{GLRT-CascadeKL-UCB}, are developed. The key idea behind the proposed algorithms is incorporating an almost parameter-free change-point detector, the Generalized Likelihood Ratio Test (GLRT), within classical upper confidence bound (UCB) based algorithms. Gap-dependent regret upper bounds of the proposed algorithms are derived, both on the order of $\mathcal{O}(\sqrt{NLT\log{T}})$, where $N$ is the number of piecewise-stationary segments, and $T$ is the time horizon. We also derive a minimax lower bound on the order of $\mathcal{O}(\sqrt{NLT})$ for piecewise-stationary CB, showing that our proposed algorithms are optimal up to a poly-logarithmic factor $\sqrt{\log T}$. Lastly, we present numerical experiments on both synthetic and real-world datasets to show that \texttt{GLRT-CascadeUCB} and \texttt{GLRT-CascadeKL-UCB} outperform state-of-the-art algorithms in the literature.

A Near-Optimal Change-Detection Based Algorithm for Piecewise-Stationary Combinatorial Semi-Bandits

We investigate the piecewise-stationary combinatorial semi-bandit problem. Compared to the original combinatorial semi-bandit problem, our setting assumes the reward distributions of base arms may change in a piecewise-stationary manner at unknown time steps. We propose an algorithm, \texttt{GLR-CUCB}, which incorporates an efficient combinatorial semi-bandit algorithm, \texttt{CUCB}, with an almost parameter-free change-point detector, the \emph{Generalized Likelihood Ratio Test} (GLRT). Our analysis shows that the regret of \texttt{GLR-CUCB} is upper bounded by $\mathcal{O}(\sqrt{NKT\log{T}})$, where $N$ is the number of piecewise-stationary segments, $K$ is the number of base arms, and $T$ is the number of time steps. As a complement, we also derive a nearly matching regret lower bound on the order of $\Omega(\sqrt{NKT}$), for both piecewise-stationary multi-armed bandits and combinatorial semi-bandits, using information-theoretic techniques and judiciously constructed piecewise-stationary bandit instances. Our lower bound is tighter than the best available regret lower bound, which is $\Omega(\sqrt{T})$. Numerical experiments on both synthetic and real-world datasets demonstrate the superiority of \texttt{GLR-CUCB} compared to other state-of-the-art algorithms.

$HS^2$: Active Learning over Hypergraphs

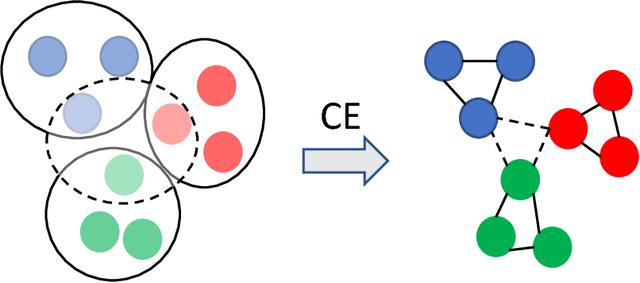
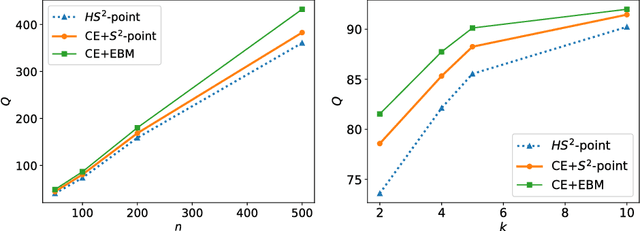
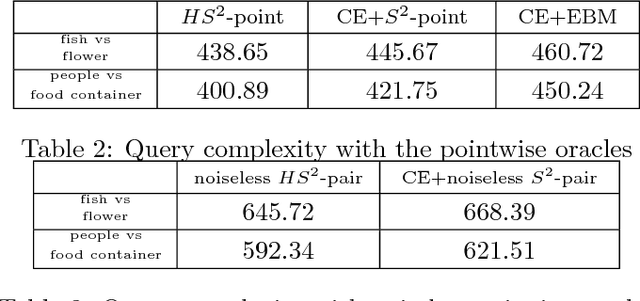
We propose a hypergraph-based active learning scheme which we term $HS^2$, $HS^2$ generalizes the previously reported algorithm $S^2$ originally proposed for graph-based active learning with pointwise queries [Dasarathy et al., COLT 2015]. Our $HS^2$ method can accommodate hypergraph structures and allows one to ask both pointwise queries and pairwise queries. Based on a novel parametric system particularly designed for hypergraphs, we derive theoretical results on the query complexity of $HS^2$ for the above described generalized settings. Both the theoretical and empirical results show that $HS^2$ requires a significantly fewer number of queries than $S^2$ when one uses $S^2$ over a graph obtained from the corresponding hypergraph via clique expansion.