$HS^2$: Active Learning over Hypergraphs

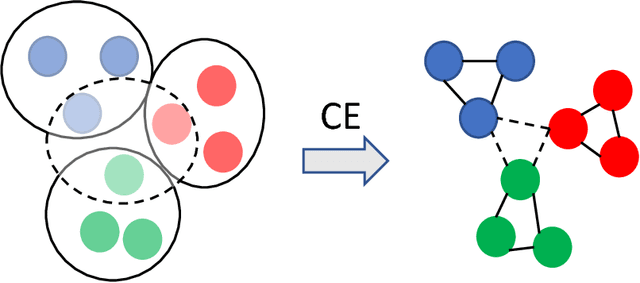
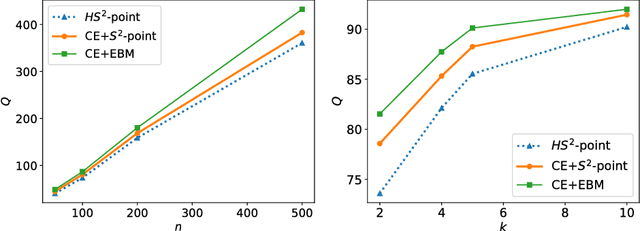
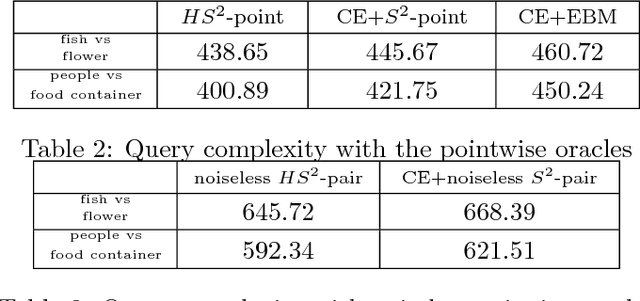
We propose a hypergraph-based active learning scheme which we term $HS^2$, $HS^2$ generalizes the previously reported algorithm $S^2$ originally proposed for graph-based active learning with pointwise queries [Dasarathy et al., COLT 2015]. Our $HS^2$ method can accommodate hypergraph structures and allows one to ask both pointwise queries and pairwise queries. Based on a novel parametric system particularly designed for hypergraphs, we derive theoretical results on the query complexity of $HS^2$ for the above described generalized settings. Both the theoretical and empirical results show that $HS^2$ requires a significantly fewer number of queries than $S^2$ when one uses $S^2$ over a graph obtained from the corresponding hypergraph via clique expansion.

Query K-means Clustering and the Double Dixie Cup Problem

We consider the problem of approximate $K$-means clustering with outliers and side information provided by same-cluster queries and possibly noisy answers. Our solution shows that, under some mild assumptions on the smallest cluster size, one can obtain an $(1+\epsilon)$-approximation for the optimal potential with probability at least $1-\delta$, where $\epsilon>0$ and $\delta\in(0,1)$, using an expected number of $O(\frac{K^3}{\epsilon \delta})$ noiseless same-cluster queries and comparison-based clustering of complexity $O(ndK + \frac{K^3}{\epsilon \delta})$, here, $n$ denotes the number of points and $d$ the dimension of space. Compared to a handful of other known approaches that perform importance sampling to account for small cluster sizes, the proposed query technique reduces the number of queries by a factor of roughly $O(\frac{K^6}{\epsilon^3})$, at the cost of possibly missing very small clusters. We extend this settings to the case where some queries to the oracle produce erroneous information, and where certain points, termed outliers, do not belong to any clusters. Our proof techniques differ from previous methods used for $K$-means clustering analysis, as they rely on estimating the sizes of the clusters and the number of points needed for accurate centroid estimation and subsequent nontrivial generalizations of the double Dixie cup problem. We illustrate the performance of the proposed algorithm both on synthetic and real datasets, including MNIST and CIFAR $10$.

On the Minimax Misclassification Ratio of Hypergraph Community Detection

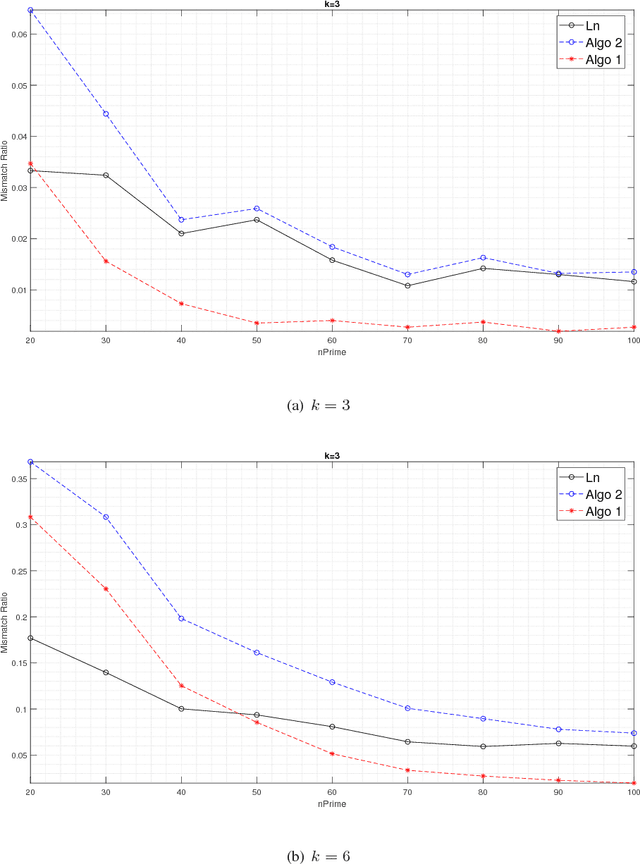
Community detection in hypergraphs is explored. Under a generative hypergraph model called "d-wise hypergraph stochastic block model" (d-hSBM) which naturally extends the Stochastic Block Model from graphs to d-uniform hypergraphs, the asymptotic minimax mismatch ratio is characterized. For proving the achievability, we propose a two-step polynomial time algorithm that achieves the fundamental limit. The first step of the algorithm is a hypergraph spectral clustering method which achieves partial recovery to a certain precision level. The second step is a local refinement method which leverages the underlying probabilistic model along with parameter estimation from the outcome of the first step. To characterize the asymptotic performance of the proposed algorithm, we first derive a sufficient condition for attaining weak consistency in the hypergraph spectral clustering step. Then, under the guarantee of weak consistency in the first step, we upper bound the worst-case risk attained in the local refinement step by an exponentially decaying function of the size of the hypergraph and characterize the decaying rate. For proving the converse, the lower bound of the minimax mismatch ratio is set by finding a smaller parameter space which contains the most dominant error events, inspired by the analysis in the achievability part. It turns out that the minimax mismatch ratio decays exponentially fast to zero as the number of nodes tends to infinity, and the rate function is a weighted combination of several divergence terms, each of which is the Renyi divergence of order 1/2 between two Bernoulli's. The Bernoulli's involved in the characterization of the rate function are those governing the random instantiation of hyperedges in d-hSBM. Experimental results on synthetic data validate our theoretical finding that the refinement step is critical in achieving the optimal statistical limit.