GUARD: Guided Unlearning and Retention via Data Attribution for Large Language Models

Unlearning in large language models (LLMs) is becoming increasingly important due to regulatory compliance, copyright protection, and privacy concerns. However, a key challenge in LLM unlearning is unintended forgetting, where the removal of specific data inadvertently impairs the utility of the model and its retention of valuable, desired information. While prior work has primarily focused on architectural innovations, the influence of data-level factors on unlearning performance remains underexplored. As a result, existing methods often suffer from degraded retention when forgetting high-impact data. To address this, we propose GUARD-a novel framework for Guided Unlearning And Retention via Data attribution. At its core, GUARD introduces a lightweight proxy data attribution metric tailored for LLM unlearning, which quantifies the "alignment" between the forget and retain sets while remaining computationally efficient. Building on this, we design a novel unlearning objective that assigns adaptive, nonuniform unlearning weights to samples, inversely proportional to their proxy attribution scores. Through such a reallocation of unlearning power, GUARD mitigates unintended losses in retention. We provide rigorous theoretical guarantees that GUARD significantly enhances retention while maintaining forgetting metrics comparable to prior methods. Extensive experiments on the TOFU benchmark across multiple LLM architectures demonstrate that GUARD substantially improves utility preservation while ensuring effective unlearning. Notably, GUARD reduces utility sacrifice on the Retain Set by up to 194.92% in terms of Truth Ratio when forgetting 10% of the training data.

Do LLMs Really Forget? Evaluating Unlearning with Knowledge Correlation and Confidence Awareness

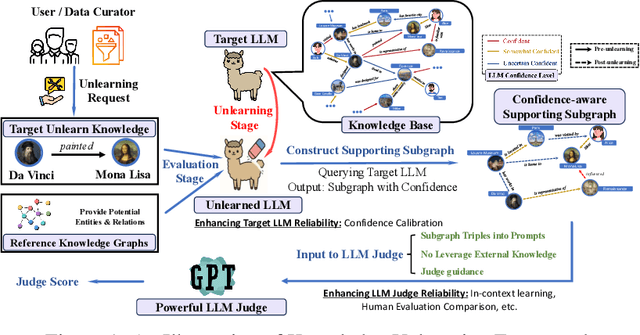
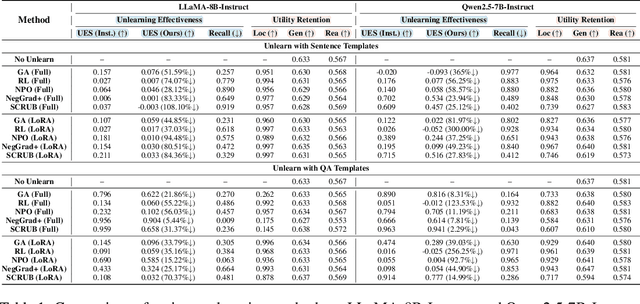
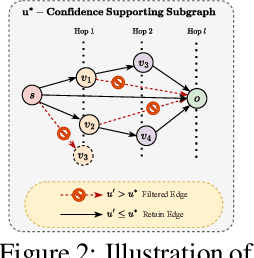
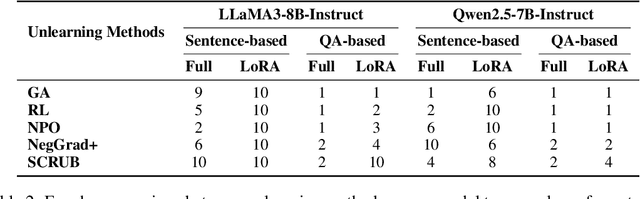
Machine unlearning techniques aim to mitigate unintended memorization in large language models (LLMs). However, existing approaches predominantly focus on the explicit removal of isolated facts, often overlooking latent inferential dependencies and the non-deterministic nature of knowledge within LLMs. Consequently, facts presumed forgotten may persist implicitly through correlated information. To address these challenges, we propose a knowledge unlearning evaluation framework that more accurately captures the implicit structure of real-world knowledge by representing relevant factual contexts as knowledge graphs with associated confidence scores. We further develop an inference-based evaluation protocol leveraging powerful LLMs as judges; these judges reason over the extracted knowledge subgraph to determine unlearning success. Our LLM judges utilize carefully designed prompts and are calibrated against human evaluations to ensure their trustworthiness and stability. Extensive experiments on our newly constructed benchmark demonstrate that our framework provides a more realistic and rigorous assessment of unlearning performance. Moreover, our findings reveal that current evaluation strategies tend to overestimate unlearning effectiveness. Our code is publicly available at https://github.com/Graph-COM/Knowledge_Unlearning.git.

DMol: A Schedule-Driven Diffusion Model for Highly Efficient and Versatile Molecule Generation

We introduce a new graph diffusion model for small molecule generation, \emph{DMol}, which outperforms the state-of-the-art DiGress model in terms of validity by roughly $1.5\%$ across all benchmarking datasets while reducing the number of diffusion steps by at least $10$-fold, and the running time to roughly one half. The performance improvements are a result of a careful change in the objective function and a ``graph noise" scheduling approach which, at each diffusion step, allows one to only change a subset of nodes of varying size in the molecule graph. Another relevant property of the method is that it can be easily combined with junction-tree-like graph representations that arise by compressing a collection of relevant ring structures into supernodes. Unlike classical junction-tree techniques that involve VAEs and require complicated reconstruction steps, compressed DMol directly performs graph diffusion on a graph that compresses only a carefully selected set of frequent carbon rings into supernodes, which results in straightforward sample generation. This compressed DMol method offers additional validity improvements over generic DMol of roughly $2\%$, increases the novelty of the method, and further improves the running time due to reductions in the graph size.

FedGTST: Boosting Global Transferability of Federated Models via Statistics Tuning

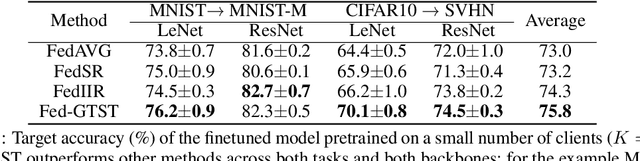
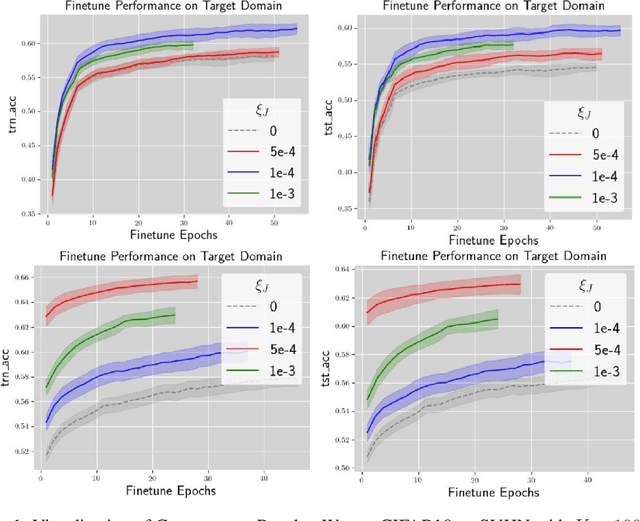
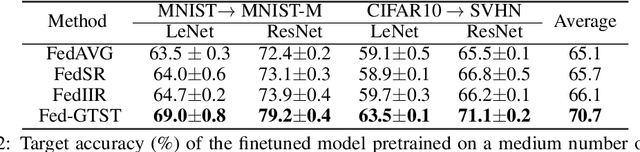
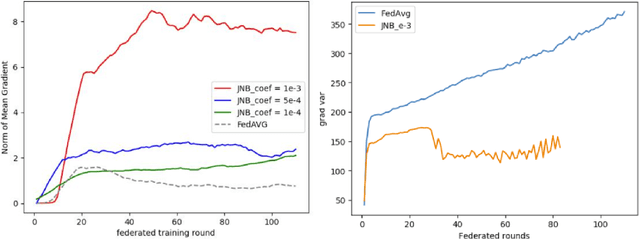
The performance of Transfer Learning (TL) heavily relies on effective pretraining, which demands large datasets and substantial computational resources. As a result, executing TL is often challenging for individual model developers. Federated Learning (FL) addresses these issues by facilitating collaborations among clients, expanding the dataset indirectly, distributing computational costs, and preserving privacy. However, key challenges remain unresolved. First, existing FL methods tend to optimize transferability only within local domains, neglecting the global learning domain. Second, most approaches rely on indirect transferability metrics, which do not accurately reflect the final target loss or true degree of transferability. To address these gaps, we propose two enhancements to FL. First, we introduce a client-server exchange protocol that leverages cross-client Jacobian (gradient) norms to boost transferability. Second, we increase the average Jacobian norm across clients at the server, using this as a local regularizer to reduce cross-client Jacobian variance. Our transferable federated algorithm, termed FedGTST (Federated Global Transferability via Statistics Tuning), demonstrates that increasing the average Jacobian and reducing its variance allows for tighter control of the target loss. This leads to an upper bound on the target loss in terms of the source loss and source-target domain discrepancy. Extensive experiments on datasets such as MNIST to MNIST-M and CIFAR10 to SVHN show that FedGTST outperforms relevant baselines, including FedSR. On the second dataset pair, FedGTST improves accuracy by 9.8% over FedSR and 7.6% over FedIIR when LeNet is used as the backbone.

Federated Aggregation of Mallows Rankings: A Comparative Analysis of Borda and Lehmer Coding

Rank aggregation combines multiple ranked lists into a consensus ranking. In fields like biomedical data sharing, rankings may be distributed and require privacy. This motivates the need for federated rank aggregation protocols, which support distributed, private, and communication-efficient learning across multiple clients with local data. We present the first known federated rank aggregation methods using Borda scoring and Lehmer codes, focusing on the sample complexity for federated algorithms on Mallows distributions with a known scaling factor $\phi$ and an unknown centroid permutation $\sigma_0$. Federated Borda approach involves local client scoring, nontrivial quantization, and privacy-preserving protocols. We show that for $\phi \in [0,1)$, and arbitrary $\sigma_0$ of length $N$, it suffices for each of the $L$ clients to locally aggregate $\max\{C_1(\phi), C_2(\phi)\frac{1}{L}\log \frac{N}{\delta}\}$ rankings, where $C_1(\phi)$ and $C_2(\phi)$ are constants, quantize the result, and send it to the server who can then recover $\sigma_0$ with probability $\geq 1-\delta$. Communication complexity scales as $NL \log N$. Our results represent the first rigorous analysis of Borda's method in centralized and distributed settings under the Mallows model. Federated Lehmer coding approach creates a local Lehmer code for each client, using a coordinate-majority aggregation approach with specialized quantization methods for efficiency and privacy. We show that for $\phi+\phi^2<1+\phi^N$, and arbitrary $\sigma_0$ of length $N$, it suffices for each of the $L$ clients to locally aggregate $\max\{C_3(\phi), C_4(\phi)\frac{1}{L}\log \frac{N}{\delta}\}$ rankings, where $C_3(\phi)$ and $C_4(\phi)$ are constants. Clients send truncated Lehmer coordinate histograms to the server, which can recover $\sigma_0$ with probability $\geq 1-\delta$. Communication complexity is $\sim O(N\log NL\log L)$.

Graph Transductive Defense: a Two-Stage Defense for Graph Membership Inference Attacks

Graph neural networks (GNNs) have become instrumental in diverse real-world applications, offering powerful graph learning capabilities for tasks such as social networks and medical data analysis. Despite their successes, GNNs are vulnerable to adversarial attacks, including membership inference attacks (MIA), which threaten privacy by identifying whether a record was part of the model's training data. While existing research has explored MIA in GNNs under graph inductive learning settings, the more common and challenging graph transductive learning setting remains understudied in this context. This paper addresses this gap and proposes an effective two-stage defense, Graph Transductive Defense (GTD), tailored to graph transductive learning characteristics. The gist of our approach is a combination of a train-test alternate training schedule and flattening strategy, which successfully reduces the difference between the training and testing loss distributions. Extensive empirical results demonstrate the superior performance of our method (a decrease in attack AUROC by $9.42\%$ and an increase in utility performance by $18.08\%$ on average compared to LBP), highlighting its potential for seamless integration into various classification models with minimal overhead.

Online Distribution Learning with Local Private Constraints

We study the problem of online conditional distribution estimation with \emph{unbounded} label sets under local differential privacy. Let $\mathcal{F}$ be a distribution-valued function class with unbounded label set. We aim at estimating an \emph{unknown} function $f\in \mathcal{F}$ in an online fashion so that at time $t$ when the context $\boldsymbol{x}_t$ is provided we can generate an estimate of $f(\boldsymbol{x}_t)$ under KL-divergence knowing only a privatized version of the true labels sampling from $f(\boldsymbol{x}_t)$. The ultimate objective is to minimize the cumulative KL-risk of a finite horizon $T$. We show that under $(\epsilon,0)$-local differential privacy of the privatized labels, the KL-risk grows as $\tilde{\Theta}(\frac{1}{\epsilon}\sqrt{KT})$ upto poly-logarithmic factors where $K=|\mathcal{F}|$. This is in stark contrast to the $\tilde{\Theta}(\sqrt{T\log K})$ bound demonstrated by Wu et al. (2023a) for bounded label sets. As a byproduct, our results recover a nearly tight upper bound for the hypothesis selection problem of gopi et al. (2020) established only for the batch setting.

Federated Classification in Hyperbolic Spaces via Secure Aggregation of Convex Hulls

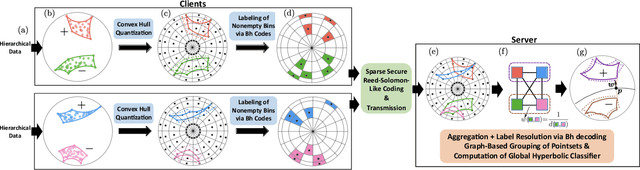
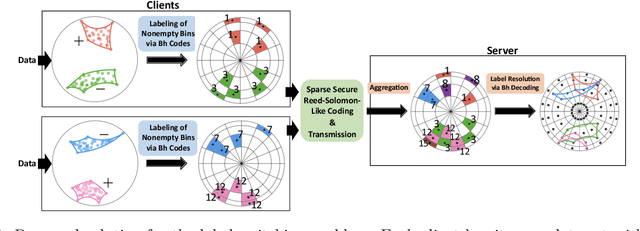
Hierarchical and tree-like data sets arise in many applications, including language processing, graph data mining, phylogeny and genomics. It is known that tree-like data cannot be embedded into Euclidean spaces of finite dimension with small distortion. This problem can be mitigated through the use of hyperbolic spaces. When such data also has to be processed in a distributed and privatized setting, it becomes necessary to work with new federated learning methods tailored to hyperbolic spaces. As an initial step towards the development of the field of federated learning in hyperbolic spaces, we propose the first known approach to federated classification in hyperbolic spaces. Our contributions are as follows. First, we develop distributed versions of convex SVM classifiers for Poincar\'e discs. In this setting, the information conveyed from clients to the global classifier are convex hulls of clusters present in individual client data. Second, to avoid label switching issues, we introduce a number-theoretic approach for label recovery based on the so-called integer $B_h$ sequences. Third, we compute the complexity of the convex hulls in hyperbolic spaces to assess the extent of data leakage; at the same time, in order to limit the communication cost for the hulls, we propose a new quantization method for the Poincar\'e disc coupled with Reed-Solomon-like encoding. Fourth, at server level, we introduce a new approach for aggregating convex hulls of the clients based on balanced graph partitioning. We test our method on a collection of diverse data sets, including hierarchical single-cell RNA-seq data from different patients distributed across different repositories that have stringent privacy constraints. The classification accuracy of our method is up to $\sim 11\%$ better than its Euclidean counterpart, demonstrating the importance of privacy-preserving learning in hyperbolic spaces.

Differentially Private Decoupled Graph Convolutions for Multigranular Topology Protection

Graph learning methods, such as Graph Neural Networks (GNNs) based on graph convolutions, are highly successful in solving real-world learning problems involving graph-structured data. However, graph learning methods expose sensitive user information and interactions not only through their model parameters but also through their model predictions. Consequently, standard Differential Privacy (DP) techniques that merely offer model weight privacy are inadequate. This is especially the case for node predictions that leverage neighboring node attributes directly via graph convolutions that create additional risks of privacy leakage. To address this problem, we introduce Graph Differential Privacy (GDP), a new formal DP framework tailored to graph learning settings that ensures both provably private model parameters and predictions. Furthermore, since there may be different privacy requirements for the node attributes and graph structure, we introduce a novel notion of relaxed node-level data adjacency. This relaxation can be used for establishing guarantees for different degrees of graph topology privacy while maintaining node attribute privacy. Importantly, this relaxation reveals a useful trade-off between utility and topology privacy for graph learning methods. In addition, our analysis of GDP reveals that existing DP-GNNs fail to exploit this trade-off due to the complex interplay between graph topology and attribute data in standard graph convolution designs. To mitigate this problem, we introduce the Differentially Private Decoupled Graph Convolution (DPDGC) model, which benefits from decoupled graph convolution while providing GDP guarantees. Extensive experiments on seven node classification benchmarking datasets demonstrate the superior privacy-utility trade-off of DPDGC over existing DP-GNNs based on standard graph convolution design.

PINA: Leveraging Side Information in eXtreme Multi-label Classification via Predicted Instance Neighborhood Aggregation

The eXtreme Multi-label Classification~(XMC) problem seeks to find relevant labels from an exceptionally large label space. Most of the existing XMC learners focus on the extraction of semantic features from input query text. However, conventional XMC studies usually neglect the side information of instances and labels, which can be of use in many real-world applications such as recommendation systems and e-commerce product search. We propose Predicted Instance Neighborhood Aggregation (PINA), a data enhancement method for the general XMC problem that leverages beneficial side information. Unlike most existing XMC frameworks that treat labels and input instances as featureless indicators and independent entries, PINA extracts information from the label metadata and the correlations among training instances. Extensive experimental results demonstrate the consistent gain of PINA on various XMC tasks compared to the state-of-the-art methods: PINA offers a gain in accuracy compared to standard XR-Transformers on five public benchmark datasets. Moreover, PINA achieves a $\sim 5\%$ gain in accuracy on the largest dataset LF-AmazonTitles-1.3M. Our implementation is publicly available.