DMol: A Schedule-Driven Diffusion Model for Highly Efficient and Versatile Molecule Generation

We introduce a new graph diffusion model for small molecule generation, \emph{DMol}, which outperforms the state-of-the-art DiGress model in terms of validity by roughly $1.5\%$ across all benchmarking datasets while reducing the number of diffusion steps by at least $10$-fold, and the running time to roughly one half. The performance improvements are a result of a careful change in the objective function and a ``graph noise" scheduling approach which, at each diffusion step, allows one to only change a subset of nodes of varying size in the molecule graph. Another relevant property of the method is that it can be easily combined with junction-tree-like graph representations that arise by compressing a collection of relevant ring structures into supernodes. Unlike classical junction-tree techniques that involve VAEs and require complicated reconstruction steps, compressed DMol directly performs graph diffusion on a graph that compresses only a carefully selected set of frequent carbon rings into supernodes, which results in straightforward sample generation. This compressed DMol method offers additional validity improvements over generic DMol of roughly $2\%$, increases the novelty of the method, and further improves the running time due to reductions in the graph size.

Federated Aggregation of Mallows Rankings: A Comparative Analysis of Borda and Lehmer Coding

Rank aggregation combines multiple ranked lists into a consensus ranking. In fields like biomedical data sharing, rankings may be distributed and require privacy. This motivates the need for federated rank aggregation protocols, which support distributed, private, and communication-efficient learning across multiple clients with local data. We present the first known federated rank aggregation methods using Borda scoring and Lehmer codes, focusing on the sample complexity for federated algorithms on Mallows distributions with a known scaling factor $\phi$ and an unknown centroid permutation $\sigma_0$. Federated Borda approach involves local client scoring, nontrivial quantization, and privacy-preserving protocols. We show that for $\phi \in [0,1)$, and arbitrary $\sigma_0$ of length $N$, it suffices for each of the $L$ clients to locally aggregate $\max\{C_1(\phi), C_2(\phi)\frac{1}{L}\log \frac{N}{\delta}\}$ rankings, where $C_1(\phi)$ and $C_2(\phi)$ are constants, quantize the result, and send it to the server who can then recover $\sigma_0$ with probability $\geq 1-\delta$. Communication complexity scales as $NL \log N$. Our results represent the first rigorous analysis of Borda's method in centralized and distributed settings under the Mallows model. Federated Lehmer coding approach creates a local Lehmer code for each client, using a coordinate-majority aggregation approach with specialized quantization methods for efficiency and privacy. We show that for $\phi+\phi^2<1+\phi^N$, and arbitrary $\sigma_0$ of length $N$, it suffices for each of the $L$ clients to locally aggregate $\max\{C_3(\phi), C_4(\phi)\frac{1}{L}\log \frac{N}{\delta}\}$ rankings, where $C_3(\phi)$ and $C_4(\phi)$ are constants. Clients send truncated Lehmer coordinate histograms to the server, which can recover $\sigma_0$ with probability $\geq 1-\delta$. Communication complexity is $\sim O(N\log NL\log L)$.

Machine Unlearning of Federated Clusters

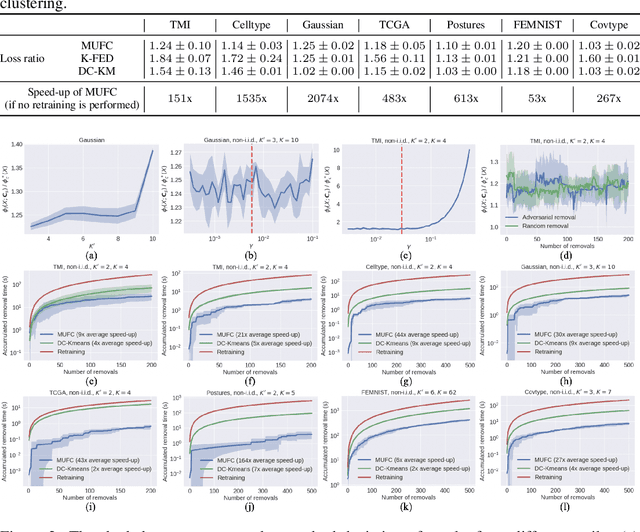
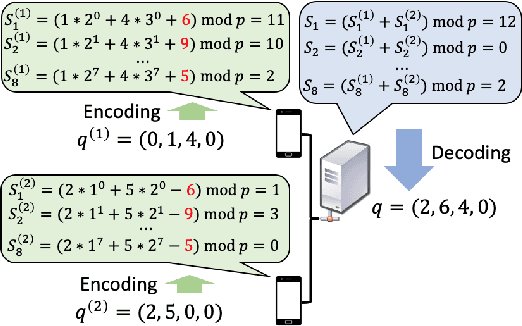
Federated clustering is an unsupervised learning problem that arises in a number of practical applications, including personalized recommender and healthcare systems. With the adoption of recent laws ensuring the "right to be forgotten", the problem of machine unlearning for federated clustering methods has become of significant importance. This work proposes the first known unlearning mechanism for federated clustering with privacy criteria that support simple, provable, and efficient data removal at the client and server level. The gist of our approach is to combine special initialization procedures with quantization methods that allow for secure aggregation of estimated local cluster counts at the server unit. As part of our platform, we introduce secure compressed multiset aggregation (SCMA), which is of independent interest for secure sparse model aggregation. In order to simultaneously facilitate low communication complexity and secret sharing protocols, we integrate Reed-Solomon encoding with special evaluation points into the new SCMA pipeline and derive bounds on the time and communication complexity of different components of the scheme. Compared to completely retraining K-means++ locally and globally for each removal request, we obtain an average speed-up of roughly 84x across seven datasets, two of which contain biological and medical information that is subject to frequent unlearning requests.