Nearest Neighbor Representations of Neural Circuits

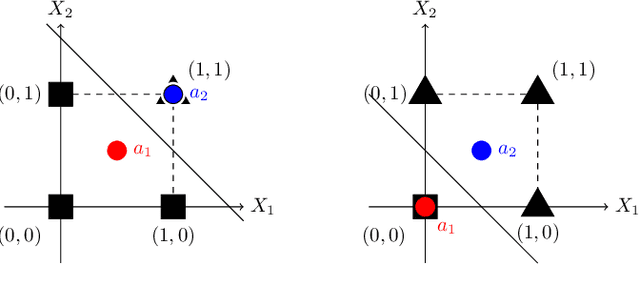
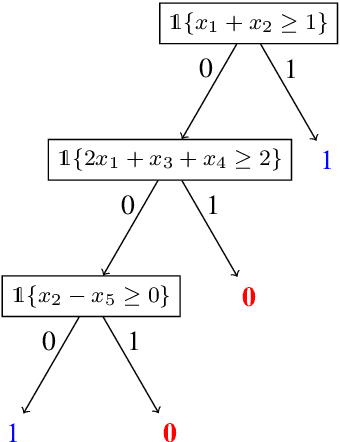
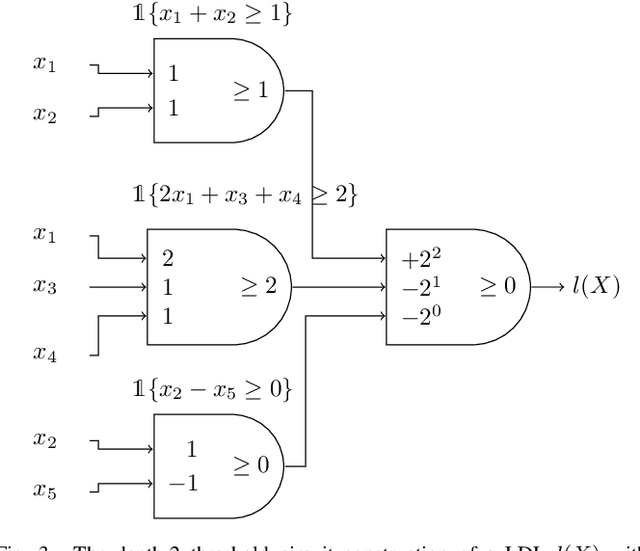
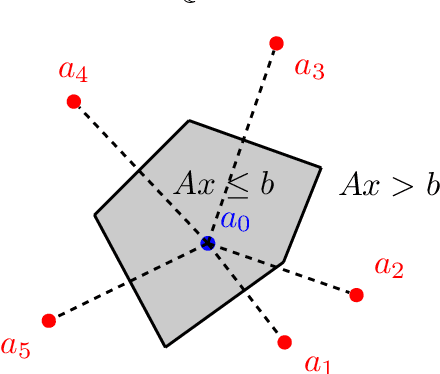
Neural networks successfully capture the computational power of the human brain for many tasks. Similarly inspired by the brain architecture, Nearest Neighbor (NN) representations is a novel approach of computation. We establish a firmer correspondence between NN representations and neural networks. Although it was known how to represent a single neuron using NN representations, there were no results even for small depth neural networks. Specifically, for depth-2 threshold circuits, we provide explicit constructions for their NN representation with an explicit bound on the number of bits to represent it. Example functions include NN representations of convex polytopes (AND of threshold gates), IP2, OR of threshold gates, and linear or exact decision lists.

Nearest Neighbor Representations of Neurons

The Nearest Neighbor (NN) Representation is an emerging computational model that is inspired by the brain. We study the complexity of representing a neuron (threshold function) using the NN representations. It is known that two anchors (the points to which NN is computed) are sufficient for a NN representation of a threshold function, however, the resolution (the maximum number of bits required for the entries of an anchor) is $O(n\log{n})$. In this work, the trade-off between the number of anchors and the resolution of a NN representation of threshold functions is investigated. We prove that the well-known threshold functions EQUALITY, COMPARISON, and ODD-MAX-BIT, which require 2 or 3 anchors and resolution of $O(n)$, can be represented by polynomially large number of anchors in $n$ and $O(\log{n})$ resolution. We conjecture that for all threshold functions, there are NN representations with polynomially large size and logarithmic resolution in $n$.

Online Distribution Learning with Local Private Constraints

We study the problem of online conditional distribution estimation with \emph{unbounded} label sets under local differential privacy. Let $\mathcal{F}$ be a distribution-valued function class with unbounded label set. We aim at estimating an \emph{unknown} function $f\in \mathcal{F}$ in an online fashion so that at time $t$ when the context $\boldsymbol{x}_t$ is provided we can generate an estimate of $f(\boldsymbol{x}_t)$ under KL-divergence knowing only a privatized version of the true labels sampling from $f(\boldsymbol{x}_t)$. The ultimate objective is to minimize the cumulative KL-risk of a finite horizon $T$. We show that under $(\epsilon,0)$-local differential privacy of the privatized labels, the KL-risk grows as $\tilde{\Theta}(\frac{1}{\epsilon}\sqrt{KT})$ upto poly-logarithmic factors where $K=|\mathcal{F}|$. This is in stark contrast to the $\tilde{\Theta}(\sqrt{T\log K})$ bound demonstrated by Wu et al. (2023a) for bounded label sets. As a byproduct, our results recover a nearly tight upper bound for the hypothesis selection problem of gopi et al. (2020) established only for the batch setting.

Oracle-Efficient Hybrid Online Learning with Unknown Distribution

We study the problem of oracle-efficient hybrid online learning when the features are generated by an unknown i.i.d. process and the labels are generated adversarially. Assuming access to an (offline) ERM oracle, we show that there exists a computationally efficient online predictor that achieves a regret upper bounded by $\tilde{O}(T^{\frac{3}{4}})$ for a finite-VC class, and upper bounded by $\tilde{O}(T^{\frac{p+1}{p+2}})$ for a class with $\alpha$ fat-shattering dimension $\alpha^{-p}$. This provides the first known oracle-efficient sublinear regret bounds for hybrid online learning with an unknown feature generation process. In particular, it confirms a conjecture of Lazaric and Munos (JCSS 2012). We then extend our result to the scenario of shifting distributions with $K$ changes, yielding a regret of order $\tilde{O}(T^{\frac{4}{5}}K^{\frac{1}{5}})$. Finally, we establish a regret of $\tilde{O}((K^{\frac{2}{3}}(\log|\mathcal{H}|)^{\frac{1}{3}}+K)\cdot T^{\frac{4}{5}})$ for the contextual $K$-armed bandits with a finite policy set $\mathcal{H}$, i.i.d. generated contexts from an unknown distribution, and adversarially generated costs.

Federated Classification in Hyperbolic Spaces via Secure Aggregation of Convex Hulls

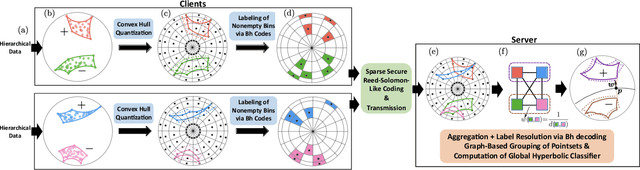
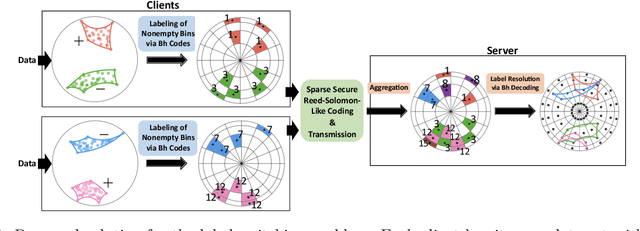
Hierarchical and tree-like data sets arise in many applications, including language processing, graph data mining, phylogeny and genomics. It is known that tree-like data cannot be embedded into Euclidean spaces of finite dimension with small distortion. This problem can be mitigated through the use of hyperbolic spaces. When such data also has to be processed in a distributed and privatized setting, it becomes necessary to work with new federated learning methods tailored to hyperbolic spaces. As an initial step towards the development of the field of federated learning in hyperbolic spaces, we propose the first known approach to federated classification in hyperbolic spaces. Our contributions are as follows. First, we develop distributed versions of convex SVM classifiers for Poincar\'e discs. In this setting, the information conveyed from clients to the global classifier are convex hulls of clusters present in individual client data. Second, to avoid label switching issues, we introduce a number-theoretic approach for label recovery based on the so-called integer $B_h$ sequences. Third, we compute the complexity of the convex hulls in hyperbolic spaces to assess the extent of data leakage; at the same time, in order to limit the communication cost for the hulls, we propose a new quantization method for the Poincar\'e disc coupled with Reed-Solomon-like encoding. Fourth, at server level, we introduce a new approach for aggregating convex hulls of the clients based on balanced graph partitioning. We test our method on a collection of diverse data sets, including hierarchical single-cell RNA-seq data from different patients distributed across different repositories that have stringent privacy constraints. The classification accuracy of our method is up to $\sim 11\%$ better than its Euclidean counterpart, demonstrating the importance of privacy-preserving learning in hyperbolic spaces.

On the Information Capacity of Nearest Neighbor Representations

The $\textit{von Neumann Computer Architecture}$ has a distinction between computation and memory. In contrast, the brain has an integrated architecture where computation and memory are indistinguishable. Motivated by the architecture of the brain, we propose a model of $\textit{associative computation}$ where memory is defined by a set of vectors in $\mathbb{R}^n$ (that we call $\textit{anchors}$), computation is performed by convergence from an input vector to a nearest neighbor anchor, and the output is a label associated with an anchor. Specifically, in this paper, we study the representation of Boolean functions in the associative computation model, where the inputs are binary vectors and the corresponding outputs are the labels ($0$ or $1$) of the nearest neighbor anchors. The information capacity of a Boolean function in this model is associated with two quantities: $\textit{(i)}$ the number of anchors (called $\textit{Nearest Neighbor (NN) Complexity}$) and $\textit{(ii)}$ the maximal number of bits representing entries of anchors (called $\textit{Resolution}$). We study symmetric Boolean functions and present constructions that have optimal NN complexity and resolution.

Machine Unlearning of Federated Clusters

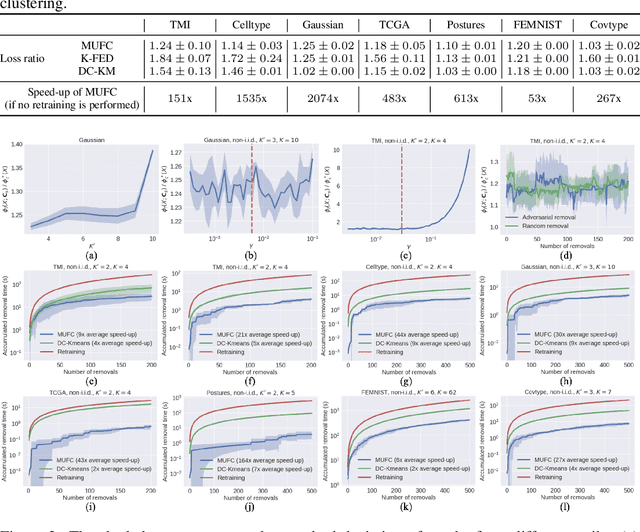
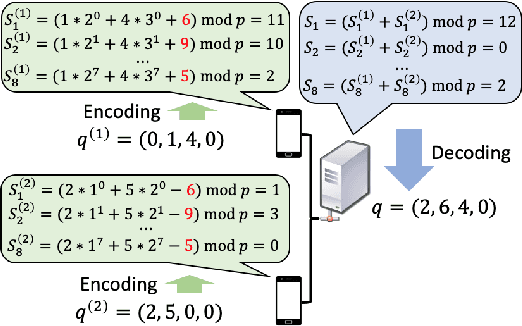
Federated clustering is an unsupervised learning problem that arises in a number of practical applications, including personalized recommender and healthcare systems. With the adoption of recent laws ensuring the "right to be forgotten", the problem of machine unlearning for federated clustering methods has become of significant importance. This work proposes the first known unlearning mechanism for federated clustering with privacy criteria that support simple, provable, and efficient data removal at the client and server level. The gist of our approach is to combine special initialization procedures with quantization methods that allow for secure aggregation of estimated local cluster counts at the server unit. As part of our platform, we introduce secure compressed multiset aggregation (SCMA), which is of independent interest for secure sparse model aggregation. In order to simultaneously facilitate low communication complexity and secret sharing protocols, we integrate Reed-Solomon encoding with special evaluation points into the new SCMA pipeline and derive bounds on the time and communication complexity of different components of the scheme. Compared to completely retraining K-means++ locally and globally for each removal request, we obtain an average speed-up of roughly 84x across seven datasets, two of which contain biological and medical information that is subject to frequent unlearning requests.

On Algebraic Constructions of Neural Networks with Small Weights

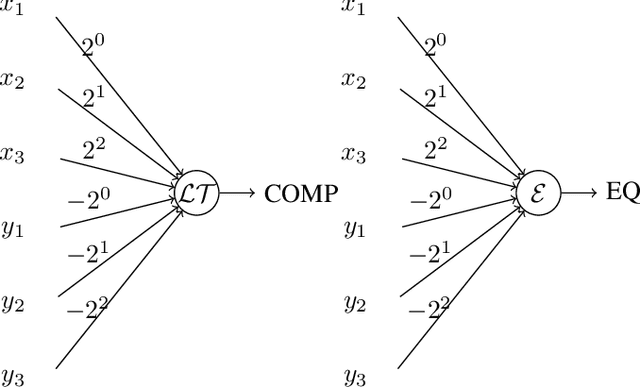
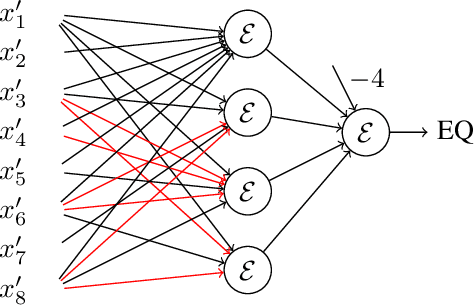
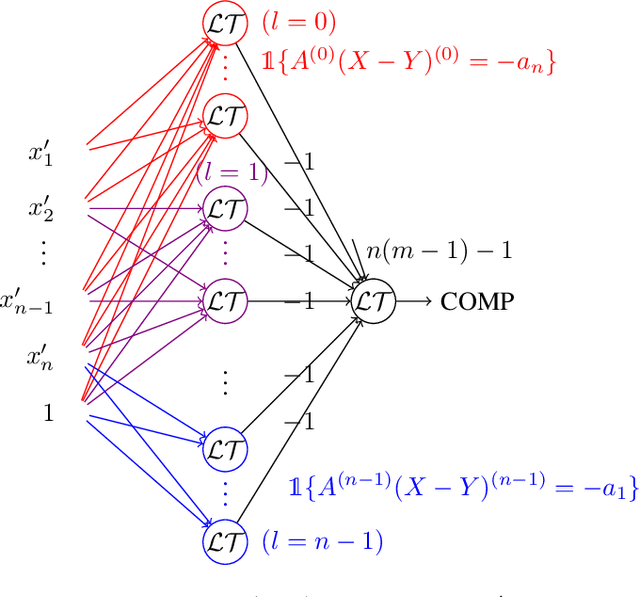
Neural gates compute functions based on weighted sums of the input variables. The expressive power of neural gates (number of distinct functions it can compute) depends on the weight sizes and, in general, large weights (exponential in the number of inputs) are required. Studying the trade-offs among the weight sizes, circuit size and depth is a well-studied topic both in circuit complexity theory and the practice of neural computation. We propose a new approach for studying these complexity trade-offs by considering a related algebraic framework. Specifically, given a single linear equation with arbitrary coefficients, we would like to express it using a system of linear equations with smaller (even constant) coefficients. The techniques we developed are based on Siegel's Lemma for the bounds, anti-concentration inequalities for the existential results and extensions of Sylvester-type Hadamard matrices for the constructions. We explicitly construct a constant weight, optimal size matrix to compute the EQUALITY function (checking if two integers expressed in binary are equal). Computing EQUALITY with a single linear equation requires exponentially large weights. In addition, we prove the existence of the best-known weight size (linear) matrices to compute the COMPARISON function (comparing between two integers expressed in binary). In the context of the circuit complexity theory, our results improve the upper bounds on the weight sizes for the best-known circuit sizes for EQUALITY and COMPARISON.