Kordag Mehmet Kilic
Nearest Neighbor Representations of Neurons
Feb 13, 2024Abstract:The Nearest Neighbor (NN) Representation is an emerging computational model that is inspired by the brain. We study the complexity of representing a neuron (threshold function) using the NN representations. It is known that two anchors (the points to which NN is computed) are sufficient for a NN representation of a threshold function, however, the resolution (the maximum number of bits required for the entries of an anchor) is $O(n\log{n})$. In this work, the trade-off between the number of anchors and the resolution of a NN representation of threshold functions is investigated. We prove that the well-known threshold functions EQUALITY, COMPARISON, and ODD-MAX-BIT, which require 2 or 3 anchors and resolution of $O(n)$, can be represented by polynomially large number of anchors in $n$ and $O(\log{n})$ resolution. We conjecture that for all threshold functions, there are NN representations with polynomially large size and logarithmic resolution in $n$.
Nearest Neighbor Representations of Neural Circuits
Feb 13, 2024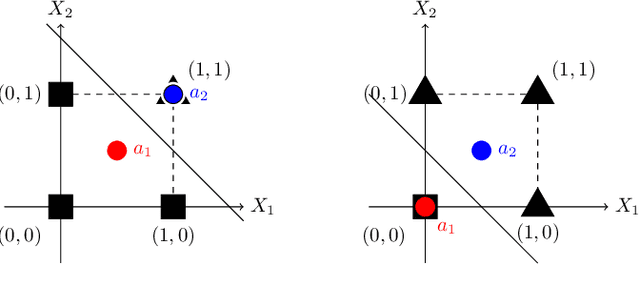
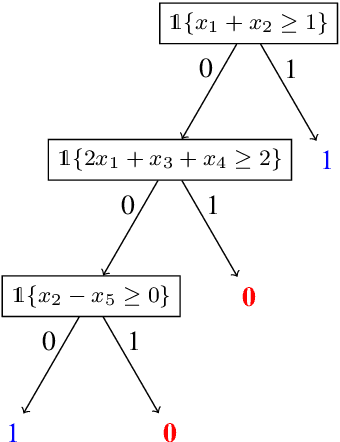
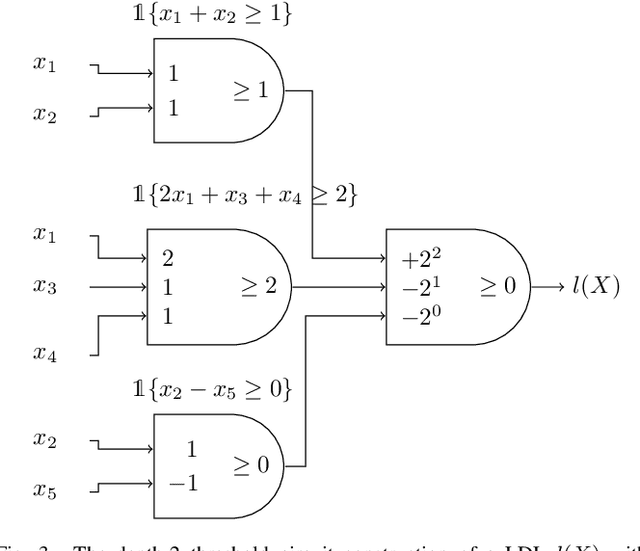
Abstract:Neural networks successfully capture the computational power of the human brain for many tasks. Similarly inspired by the brain architecture, Nearest Neighbor (NN) representations is a novel approach of computation. We establish a firmer correspondence between NN representations and neural networks. Although it was known how to represent a single neuron using NN representations, there were no results even for small depth neural networks. Specifically, for depth-2 threshold circuits, we provide explicit constructions for their NN representation with an explicit bound on the number of bits to represent it. Example functions include NN representations of convex polytopes (AND of threshold gates), IP2, OR of threshold gates, and linear or exact decision lists.
On the Information Capacity of Nearest Neighbor Representations
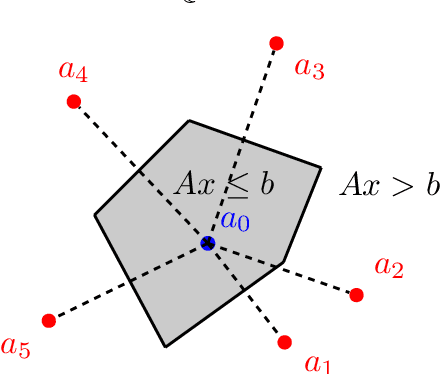
May 09, 2023Abstract:The $\textit{von Neumann Computer Architecture}$ has a distinction between computation and memory. In contrast, the brain has an integrated architecture where computation and memory are indistinguishable. Motivated by the architecture of the brain, we propose a model of $\textit{associative computation}$ where memory is defined by a set of vectors in $\mathbb{R}^n$ (that we call $\textit{anchors}$), computation is performed by convergence from an input vector to a nearest neighbor anchor, and the output is a label associated with an anchor. Specifically, in this paper, we study the representation of Boolean functions in the associative computation model, where the inputs are binary vectors and the corresponding outputs are the labels ($0$ or $1$) of the nearest neighbor anchors. The information capacity of a Boolean function in this model is associated with two quantities: $\textit{(i)}$ the number of anchors (called $\textit{Nearest Neighbor (NN) Complexity}$) and $\textit{(ii)}$ the maximal number of bits representing entries of anchors (called $\textit{Resolution}$). We study symmetric Boolean functions and present constructions that have optimal NN complexity and resolution.
On Algebraic Constructions of Neural Networks with Small Weights
May 17, 2022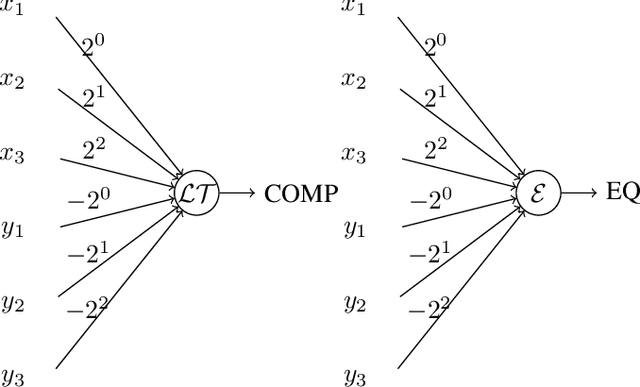
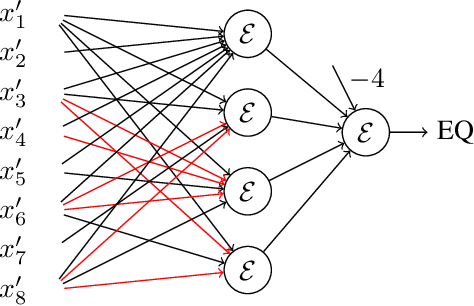
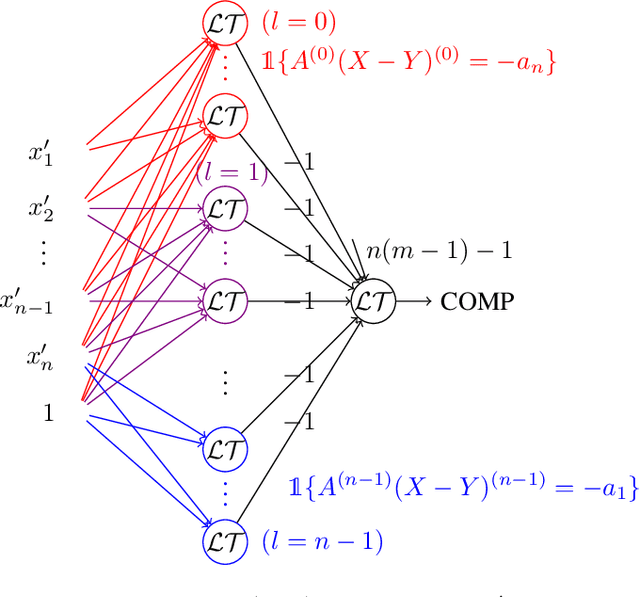

Abstract:Neural gates compute functions based on weighted sums of the input variables. The expressive power of neural gates (number of distinct functions it can compute) depends on the weight sizes and, in general, large weights (exponential in the number of inputs) are required. Studying the trade-offs among the weight sizes, circuit size and depth is a well-studied topic both in circuit complexity theory and the practice of neural computation. We propose a new approach for studying these complexity trade-offs by considering a related algebraic framework. Specifically, given a single linear equation with arbitrary coefficients, we would like to express it using a system of linear equations with smaller (even constant) coefficients. The techniques we developed are based on Siegel's Lemma for the bounds, anti-concentration inequalities for the existential results and extensions of Sylvester-type Hadamard matrices for the constructions. We explicitly construct a constant weight, optimal size matrix to compute the EQUALITY function (checking if two integers expressed in binary are equal). Computing EQUALITY with a single linear equation requires exponentially large weights. In addition, we prove the existence of the best-known weight size (linear) matrices to compute the COMPARISON function (comparing between two integers expressed in binary). In the context of the circuit complexity theory, our results improve the upper bounds on the weight sizes for the best-known circuit sizes for EQUALITY and COMPARISON.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge