$HS^2$: Active Learning over Hypergraphs

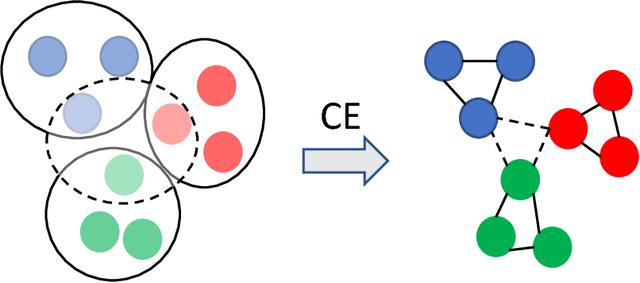
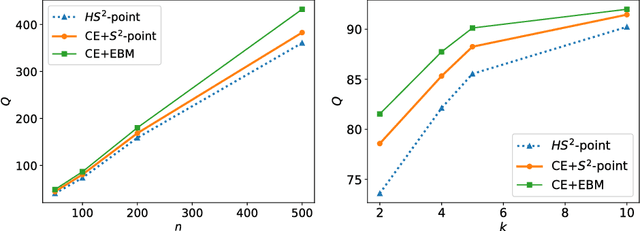
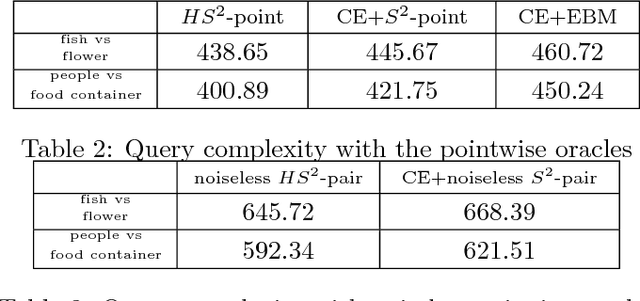
We propose a hypergraph-based active learning scheme which we term $HS^2$, $HS^2$ generalizes the previously reported algorithm $S^2$ originally proposed for graph-based active learning with pointwise queries [Dasarathy et al., COLT 2015]. Our $HS^2$ method can accommodate hypergraph structures and allows one to ask both pointwise queries and pairwise queries. Based on a novel parametric system particularly designed for hypergraphs, we derive theoretical results on the query complexity of $HS^2$ for the above described generalized settings. Both the theoretical and empirical results show that $HS^2$ requires a significantly fewer number of queries than $S^2$ when one uses $S^2$ over a graph obtained from the corresponding hypergraph via clique expansion.