Chung-Yi Lin
Improving Generalization Ability for 3D Object Detection by Learning Sparsity-invariant Features
Feb 04, 2025Abstract:In autonomous driving, 3D object detection is essential for accurately identifying and tracking objects. Despite the continuous development of various technologies for this task, a significant drawback is observed in most of them-they experience substantial performance degradation when detecting objects in unseen domains. In this paper, we propose a method to improve the generalization ability for 3D object detection on a single domain. We primarily focus on generalizing from a single source domain to target domains with distinct sensor configurations and scene distributions. To learn sparsity-invariant features from a single source domain, we selectively subsample the source data to a specific beam, using confidence scores determined by the current detector to identify the density that holds utmost importance for the detector. Subsequently, we employ the teacher-student framework to align the Bird's Eye View (BEV) features for different point clouds densities. We also utilize feature content alignment (FCA) and graph-based embedding relationship alignment (GERA) to instruct the detector to be domain-agnostic. Extensive experiments demonstrate that our method exhibits superior generalization capabilities compared to other baselines. Furthermore, our approach even outperforms certain domain adaptation methods that can access to the target domain data.
Tracking-Assisted Object Detection with Event Cameras
Mar 27, 2024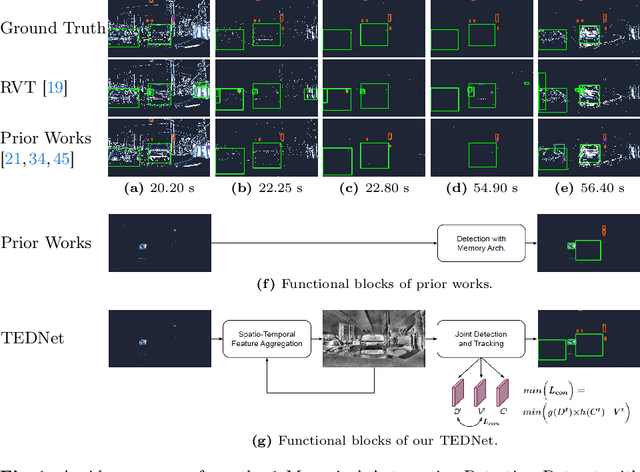

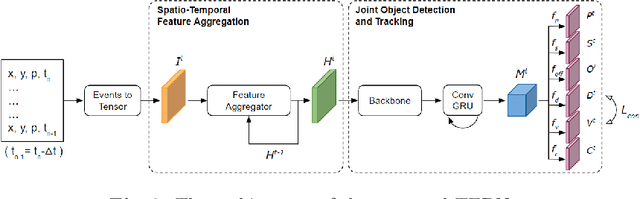

Abstract:Event-based object detection has recently garnered attention in the computer vision community due to the exceptional properties of event cameras, such as high dynamic range and no motion blur. However, feature asynchronism and sparsity cause invisible objects due to no relative motion to the camera, posing a significant challenge in the task. Prior works have studied various memory mechanisms to preserve as many features as possible at the current time, guided by temporal clues. While these implicit-learned memories retain some short-term information, they still struggle to preserve long-term features effectively. In this paper, we consider those invisible objects as pseudo-occluded objects and aim to reveal their features. Firstly, we introduce visibility attribute of objects and contribute an auto-labeling algorithm to append additional visibility labels on an existing event camera dataset. Secondly, we exploit tracking strategies for pseudo-occluded objects to maintain their permanence and retain their bounding boxes, even when features have not been available for a very long time. These strategies can be treated as an explicit-learned memory guided by the tracking objective to record the displacements of objects across frames. Lastly, we propose a spatio-temporal feature aggregation module to enrich the latent features and a consistency loss to increase the robustness of the overall pipeline. We conduct comprehensive experiments to verify our method's effectiveness where still objects are retained but real occluded objects are discarded. The results demonstrate that (1) the additional visibility labels can assist in supervised training, and (2) our method outperforms state-of-the-art approaches with a significant improvement of 7.9% absolute mAP.
Multivariate and Propagation Graph Attention Network for Spatial-Temporal Prediction with Outdoor Cellular Traffic
Aug 23, 2021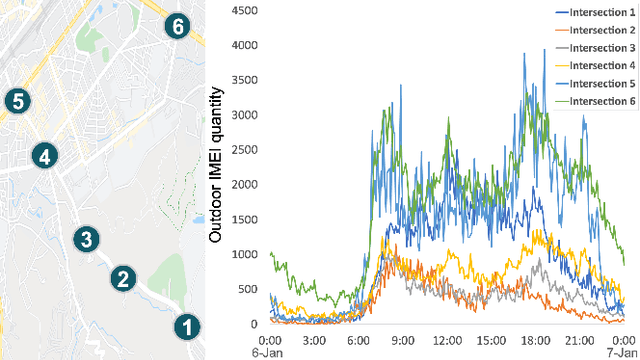

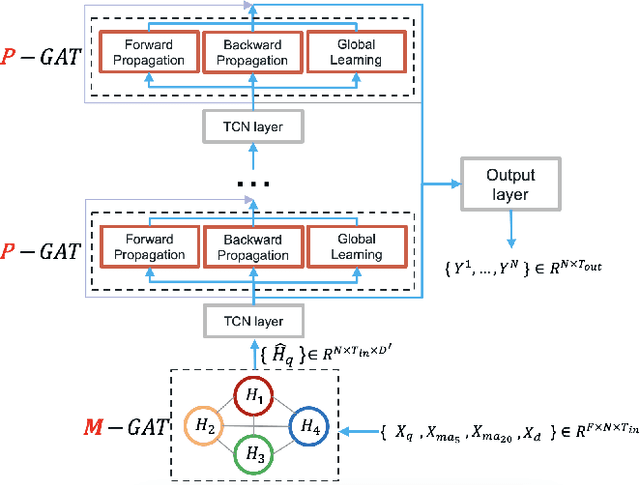
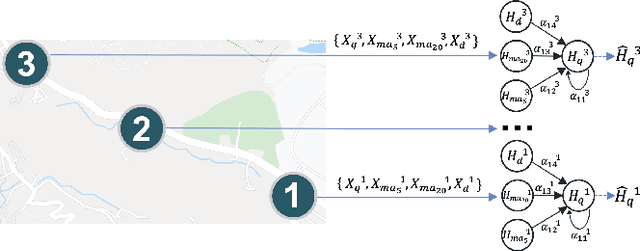
Abstract:Spatial-temporal prediction is a critical problem for intelligent transportation, which is helpful for tasks such as traffic control and accident prevention. Previous studies rely on large-scale traffic data collected from sensors. However, it is unlikely to deploy sensors in all regions due to the device and maintenance costs. This paper addresses the problem via outdoor cellular traffic distilled from over two billion records per day in a telecom company, because outdoor cellular traffic induced by user mobility is highly related to transportation traffic. We study road intersections in urban and aim to predict future outdoor cellular traffic of all intersections given historic outdoor cellular traffic. Furthermore, we propose a new model for multivariate spatial-temporal prediction, mainly consisting of two extending graph attention networks (GAT). First GAT is used to explore correlations among multivariate cellular traffic. Another GAT leverages the attention mechanism into graph propagation to increase the efficiency of capturing spatial dependency. Experiments show that the proposed model significantly outperforms the state-of-the-art methods on our dataset.
Achieving the fundamental convergence-communication tradeoff with Differentially Quantized Gradient Descent
Feb 06, 2020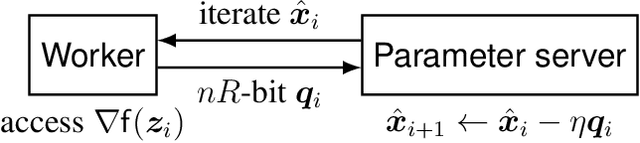

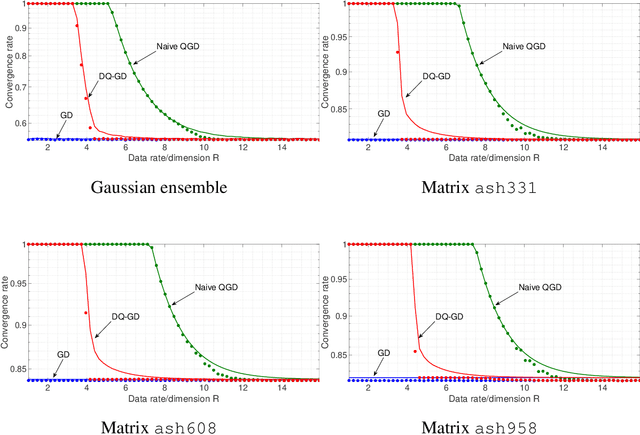
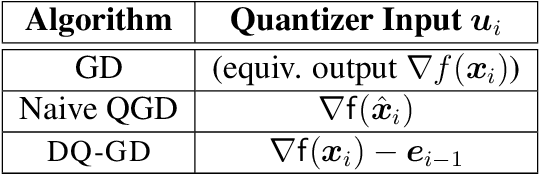
Abstract:The problem of reducing the communication cost in distributed training through gradient quantization is considered. For the class of smooth and strongly convex objective functions, we characterize the minimum achievable linear convergence rate for a given number of bits per problem dimension $n$. We propose Differentially Quantized Gradient Descent, a quantization algorithm with error compensation, and prove that it achieves the fundamental tradeoff between communication rate and convergence rate as $n$ goes to infinity. In contrast, the naive quantizer that compresses the current gradient directly fails to achieve that optimal tradeoff. Experimental results on both simulated and real-world least-squares problems confirm our theoretical analysis.
On the Minimax Misclassification Ratio of Hypergraph Community Detection
Feb 03, 2018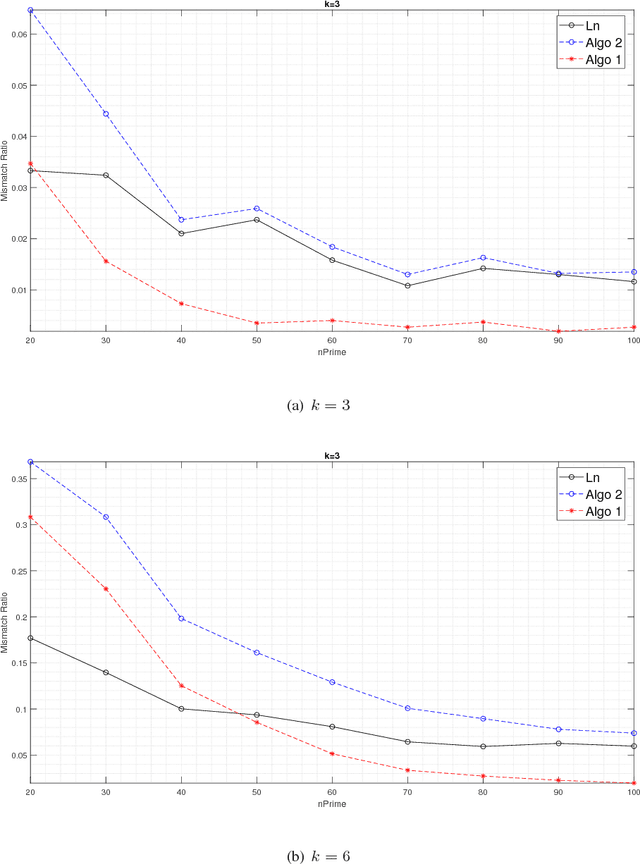
Abstract:Community detection in hypergraphs is explored. Under a generative hypergraph model called "d-wise hypergraph stochastic block model" (d-hSBM) which naturally extends the Stochastic Block Model from graphs to d-uniform hypergraphs, the asymptotic minimax mismatch ratio is characterized. For proving the achievability, we propose a two-step polynomial time algorithm that achieves the fundamental limit. The first step of the algorithm is a hypergraph spectral clustering method which achieves partial recovery to a certain precision level. The second step is a local refinement method which leverages the underlying probabilistic model along with parameter estimation from the outcome of the first step. To characterize the asymptotic performance of the proposed algorithm, we first derive a sufficient condition for attaining weak consistency in the hypergraph spectral clustering step. Then, under the guarantee of weak consistency in the first step, we upper bound the worst-case risk attained in the local refinement step by an exponentially decaying function of the size of the hypergraph and characterize the decaying rate. For proving the converse, the lower bound of the minimax mismatch ratio is set by finding a smaller parameter space which contains the most dominant error events, inspired by the analysis in the achievability part. It turns out that the minimax mismatch ratio decays exponentially fast to zero as the number of nodes tends to infinity, and the rate function is a weighted combination of several divergence terms, each of which is the Renyi divergence of order 1/2 between two Bernoulli's. The Bernoulli's involved in the characterization of the rate function are those governing the random instantiation of hyperedges in d-hSBM. Experimental results on synthetic data validate our theoretical finding that the refinement step is critical in achieving the optimal statistical limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge