Babak Hassibi
Concentration of Measure for Distributions Generated via Diffusion Models
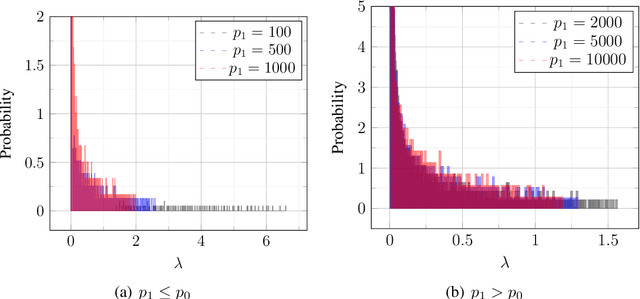
Jan 13, 2025Abstract:We show via a combination of mathematical arguments and empirical evidence that data distributions sampled from diffusion models satisfy a Concentration of Measure Property saying that any Lipschitz $1$-dimensional projection of a random vector is not too far from its mean with high probability. This implies that such models are quite restrictive and gives an explanation for a fact previously observed in arXiv:2410.14171 that conventional diffusion models cannot capture "heavy-tailed" data (i.e. data $\mathbf{x}$ for which the norm $\|\mathbf{x}\|_2$ does not possess a subgaussian tail) well. We then proceed to train a generalized linear model using stochastic gradient descent (SGD) on the diffusion-generated data for a multiclass classification task and observe empirically that a Gaussian universality result holds for the test error. In other words, the test error depends only on the first and second order statistics of the diffusion-generated data in the linear setting. Results of such forms are desirable because they allow one to assume the data itself is Gaussian for analyzing performance of the trained classifier. Finally, we note that current approaches to proving universality do not apply to this case as the covariance matrices of the data tend to have vanishing minimum singular values for the diffusion-generated data, while the current proofs assume that this is not the case (see Subsection 3.4 for more details). This leaves extending previous mathematical universality results as an intriguing open question.
Universality in Transfer Learning for Linear Models
Oct 03, 2024Abstract:Transfer learning is an attractive framework for problems where there is a paucity of data, or where data collection is costly. One common approach to transfer learning is referred to as "model-based", and involves using a model that is pretrained on samples from a source distribution, which is easier to acquire, and then fine-tuning the model on a few samples from the target distribution. The hope is that, if the source and target distributions are ``close", then the fine-tuned model will perform well on the target distribution even though it has seen only a few samples from it. In this work, we study the problem of transfer learning in linear models for both regression and binary classification. In particular, we consider the use of stochastic gradient descent (SGD) on a linear model initialized with pretrained weights and using a small training data set from the target distribution. In the asymptotic regime of large models, we provide an exact and rigorous analysis and relate the generalization errors (in regression) and classification errors (in binary classification) for the pretrained and fine-tuned models. In particular, we give conditions under which the fine-tuned model outperforms the pretrained one. An important aspect of our work is that all the results are "universal", in the sense that they depend only on the first and second order statistics of the target distribution. They thus extend well beyond the standard Gaussian assumptions commonly made in the literature.
Distributionally Robust Kalman Filtering over Finite and Infinite Horizon
Jul 26, 2024Abstract:This paper investigates the distributionally robust filtering of signals generated by state-space models driven by exogenous disturbances with noisy observations in finite and infinite horizon scenarios. The exact joint probability distribution of the disturbances and noise is unknown but assumed to reside within a Wasserstein-2 ambiguity ball centered around a given nominal distribution. We aim to derive a causal estimator that minimizes the worst-case mean squared estimation error among all possible distributions within this ambiguity set. We remove the iid restriction in prior works by permitting arbitrarily time-correlated disturbances and noises. In the finite horizon setting, we reduce this problem to a semi-definite program (SDP), with computational complexity scaling with the time horizon. For infinite horizon settings, we characterize the optimal estimator using Karush-Kuhn-Tucker (KKT) conditions. Although the optimal estimator lacks a rational form, i.e., a finite-dimensional state-space realization, it can be fully described by a finite-dimensional parameter. {Leveraging this parametrization, we propose efficient algorithms that compute the optimal estimator with arbitrary fidelity in the frequency domain.} Moreover, given any finite degree, we provide an efficient convex optimization algorithm that finds the finite-dimensional state-space estimator that best approximates the optimal non-rational filter in ${\cal H}_\infty$ norm. This facilitates the practical implementation of the infinite horizon filter without having to grapple with the ill-scaled SDP from finite time. Finally, numerical simulations demonstrate the effectiveness of our approach in practical scenarios.
One-Bit Quantization and Sparsification for Multiclass Linear Classification via Regularized Regression
Feb 16, 2024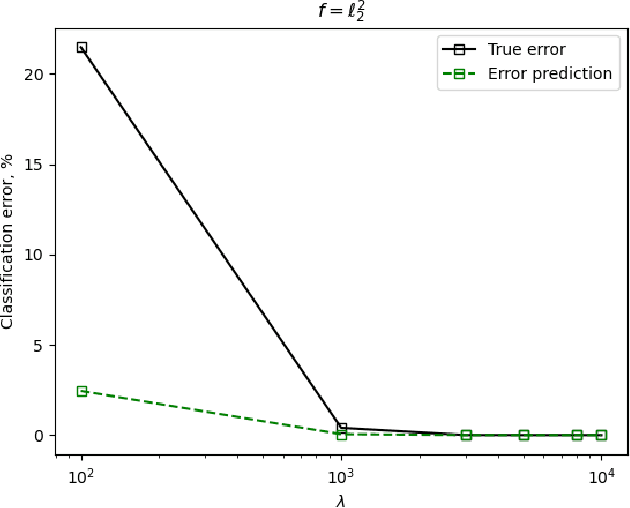
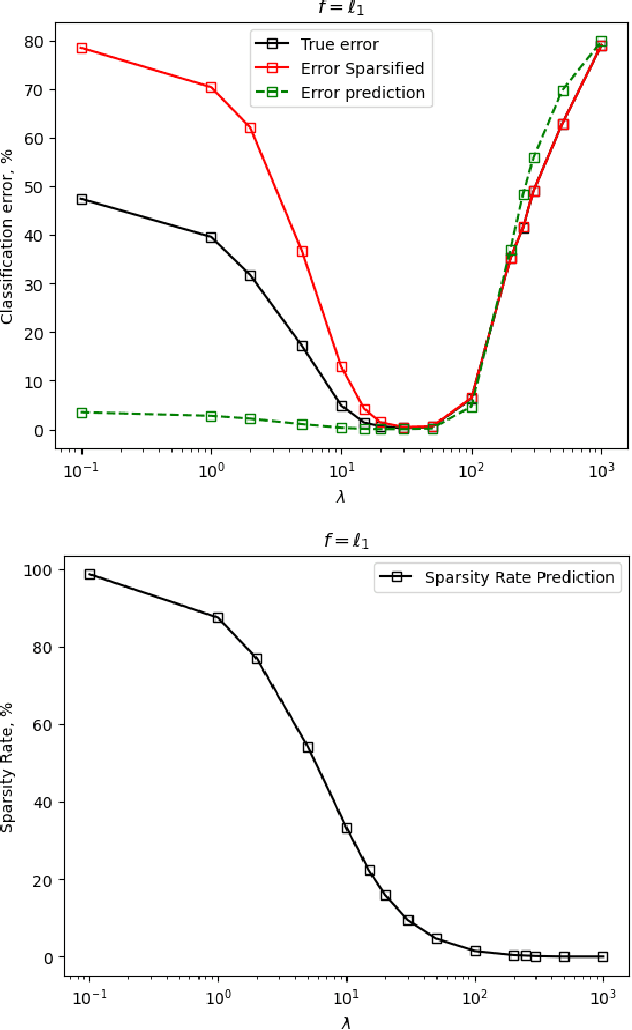
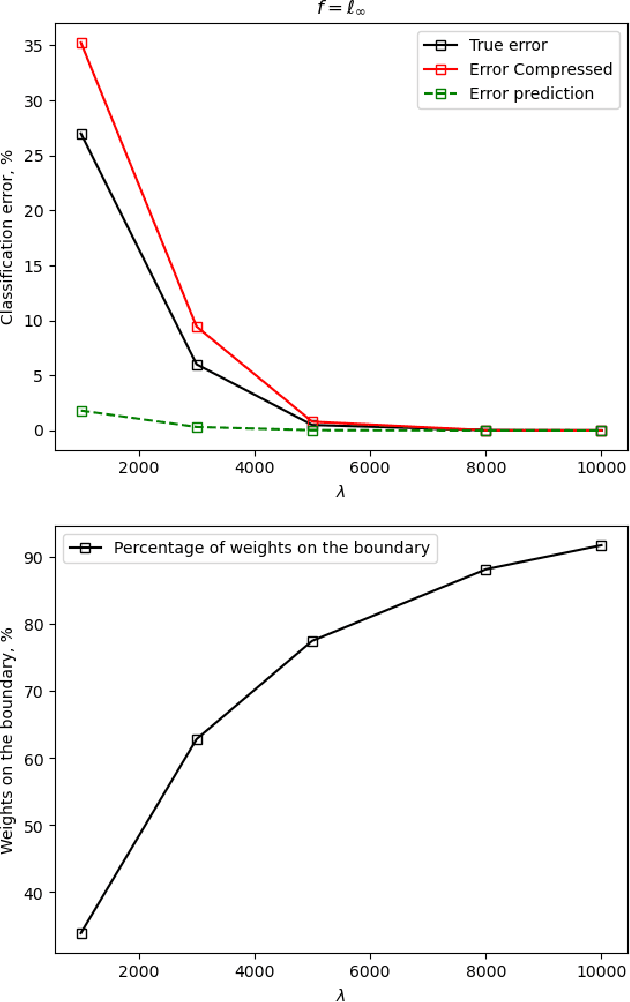
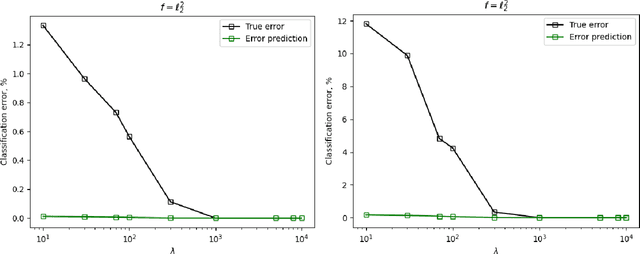
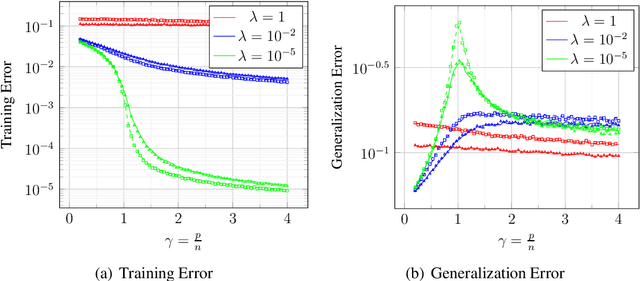
Abstract:We study the use of linear regression for multiclass classification in the over-parametrized regime where some of the training data is mislabeled. In such scenarios it is necessary to add an explicit regularization term, $\lambda f(w)$, for some convex function $f(\cdot)$, to avoid overfitting the mislabeled data. In our analysis, we assume that the data is sampled from a Gaussian Mixture Model with equal class sizes, and that a proportion $c$ of the training labels is corrupted for each class. Under these assumptions, we prove that the best classification performance is achieved when $f(\cdot) = \|\cdot\|^2_2$ and $\lambda \to \infty$. We then proceed to analyze the classification errors for $f(\cdot) = \|\cdot\|_1$ and $f(\cdot) = \|\cdot\|_\infty$ in the large $\lambda$ regime and notice that it is often possible to find sparse and one-bit solutions, respectively, that perform almost as well as the one corresponding to $f(\cdot) = \|\cdot\|_2^2$.
A Novel Gaussian Min-Max Theorem and its Applications
Feb 12, 2024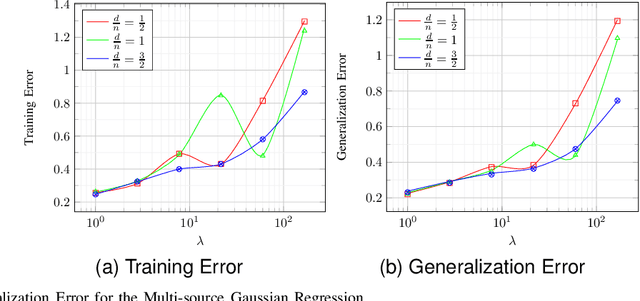
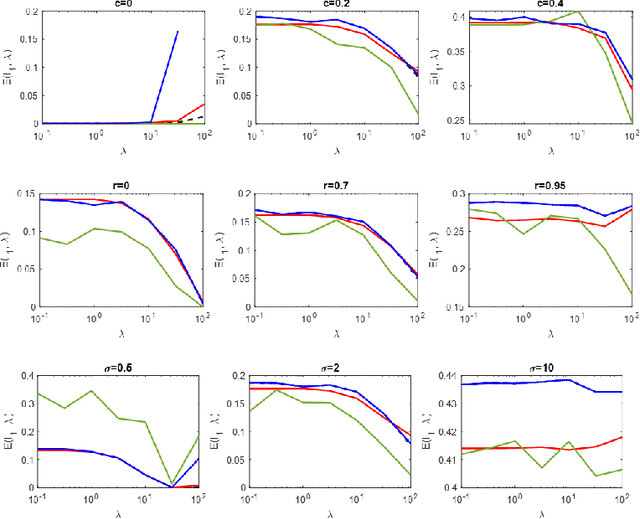
Abstract:A celebrated result by Gordon allows one to compare the min-max behavior of two Gaussian processes if certain inequality conditions are met. The consequences of this result include the Gaussian min-max (GMT) and convex Gaussian min-max (CGMT) theorems which have had far-reaching implications in high-dimensional statistics, machine learning, non-smooth optimization, and signal processing. Both theorems rely on a pair of Gaussian processes, first identified by Slepian, that satisfy Gordon's comparison inequalities. To date, no other pair of Gaussian processes satisfying these inequalities has been discovered. In this paper, we identify such a new pair. The resulting theorems extend the classical GMT and CGMT Theorems from the case where the underlying Gaussian matrix in the primary process has iid rows to where it has independent but non-identically-distributed ones. The new CGMT is applied to the problems of multi-source Gaussian regression, as well as to binary classification of general Gaussian mixture models.
Regularized Linear Regression for Binary Classification
Nov 03, 2023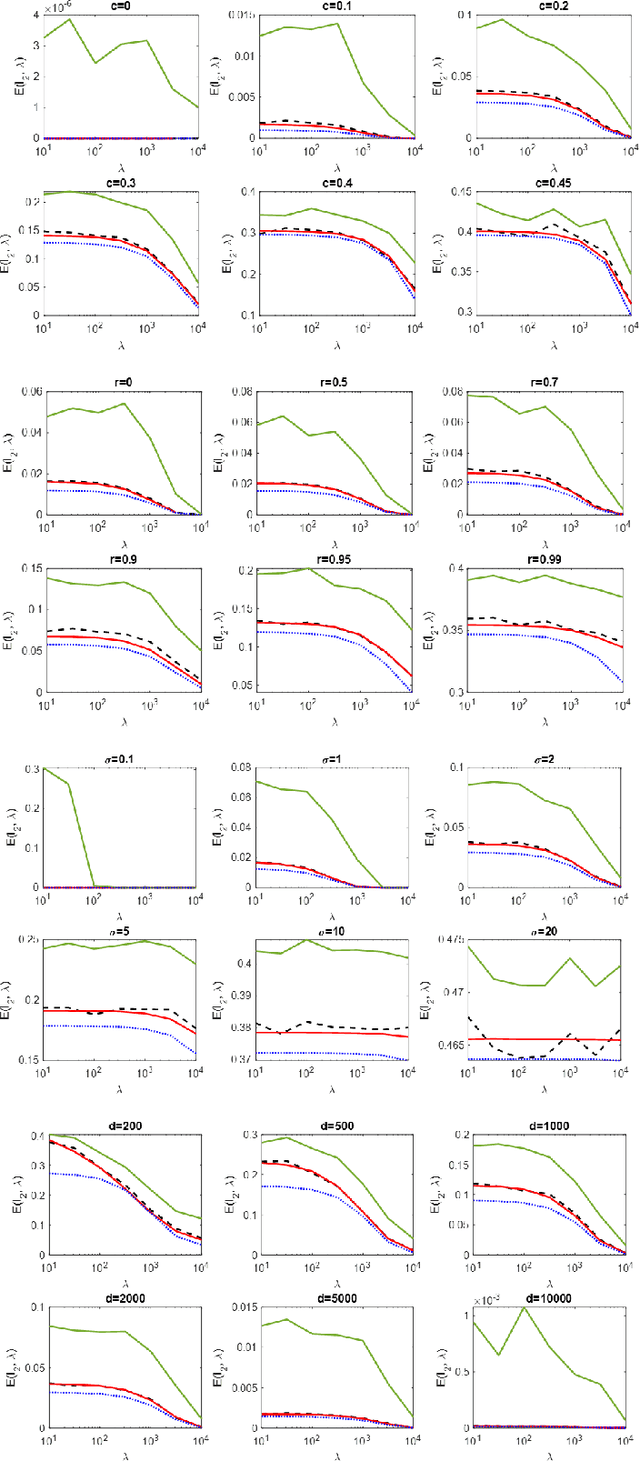
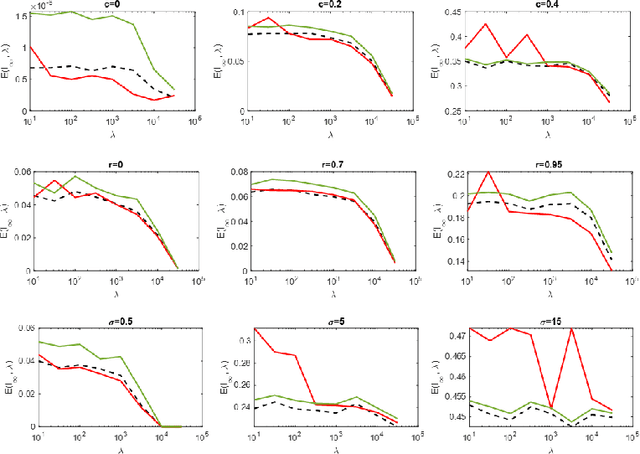
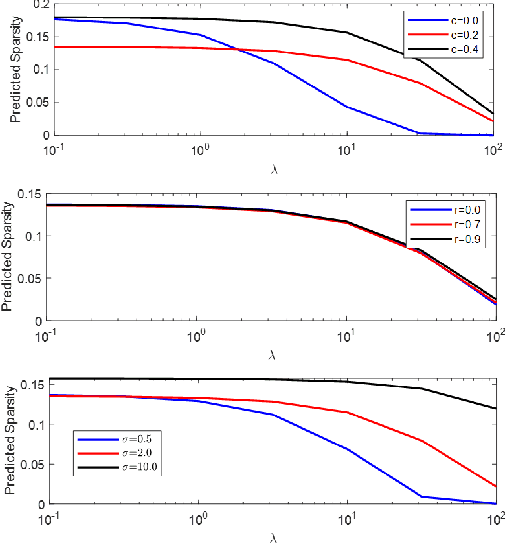
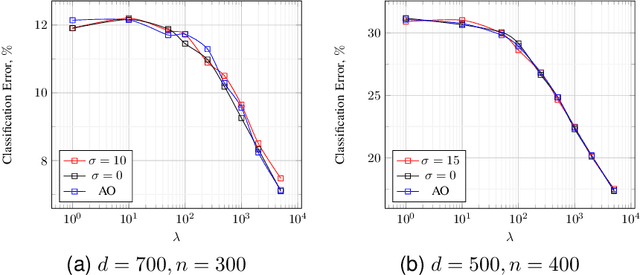
Abstract:Regularized linear regression is a promising approach for binary classification problems in which the training set has noisy labels since the regularization term can help to avoid interpolating the mislabeled data points. In this paper we provide a systematic study of the effects of the regularization strength on the performance of linear classifiers that are trained to solve binary classification problems by minimizing a regularized least-squares objective. We consider the over-parametrized regime and assume that the classes are generated from a Gaussian Mixture Model (GMM) where a fraction $c<\frac{1}{2}$ of the training data is mislabeled. Under these assumptions, we rigorously analyze the classification errors resulting from the application of ridge, $\ell_1$, and $\ell_\infty$ regression. In particular, we demonstrate that ridge regression invariably improves the classification error. We prove that $\ell_1$ regularization induces sparsity and observe that in many cases one can sparsify the solution by up to two orders of magnitude without any considerable loss of performance, even though the GMM has no underlying sparsity structure. For $\ell_\infty$ regularization we show that, for large enough regularization strength, the optimal weights concentrate around two values of opposite sign. We observe that in many cases the corresponding "compression" of each weight to a single bit leads to very little loss in performance. These latter observations can have significant practical ramifications.
The Generalization Error of Stochastic Mirror Descent on Over-Parametrized Linear Models
Feb 18, 2023Abstract:Despite being highly over-parametrized, and having the ability to fully interpolate the training data, deep networks are known to generalize well to unseen data. It is now understood that part of the reason for this is that the training algorithms used have certain implicit regularization properties that ensure interpolating solutions with "good" properties are found. This is best understood in linear over-parametrized models where it has been shown that the celebrated stochastic gradient descent (SGD) algorithm finds an interpolating solution that is closest in Euclidean distance to the initial weight vector. Different regularizers, replacing Euclidean distance with Bregman divergence, can be obtained if we replace SGD with stochastic mirror descent (SMD). Empirical observations have shown that in the deep network setting, SMD achieves a generalization performance that is different from that of SGD (and which depends on the choice of SMD's potential function. In an attempt to begin to understand this behavior, we obtain the generalization error of SMD for over-parametrized linear models for a binary classification problem where the two classes are drawn from a Gaussian mixture model. We present simulation results that validate the theory and, in particular, introduce two data models, one for which SMD with an $\ell_2$ regularizer (i.e., SGD) outperforms SMD with an $\ell_1$ regularizer, and one for which the reverse happens.
Precise Asymptotic Analysis of Deep Random Feature Models
Feb 13, 2023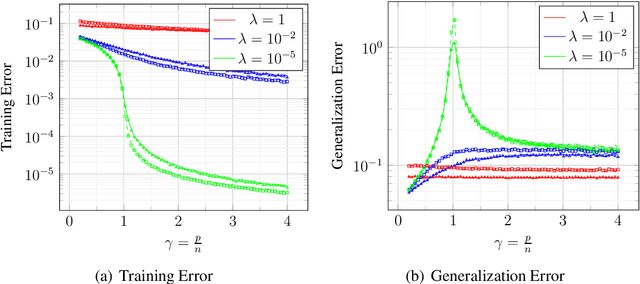
Abstract:We provide exact asymptotic expressions for the performance of regression by an $L-$layer deep random feature (RF) model, where the input is mapped through multiple random embedding and non-linear activation functions. For this purpose, we establish two key steps: First, we prove a novel universality result for RF models and deterministic data, by which we demonstrate that a deep random feature model is equivalent to a deep linear Gaussian model that matches it in the first and second moments, at each layer. Second, we make use of the convex Gaussian Min-Max theorem multiple times to obtain the exact behavior of deep RF models. We further characterize the variation of the eigendistribution in different layers of the equivalent Gaussian model, demonstrating that depth has a tangible effect on model performance despite the fact that only the last layer of the model is being trained.
Stochastic Mirror Descent in Average Ensemble Models
Oct 27, 2022Abstract:The stochastic mirror descent (SMD) algorithm is a general class of training algorithms, which includes the celebrated stochastic gradient descent (SGD), as a special case. It utilizes a mirror potential to influence the implicit bias of the training algorithm. In this paper we explore the performance of the SMD iterates on mean-field ensemble models. Our results generalize earlier ones obtained for SGD on such models. The evolution of the distribution of parameters is mapped to a continuous time process in the space of probability distributions. Our main result gives a nonlinear partial differential equation to which the continuous time process converges in the asymptotic regime of large networks. The impact of the mirror potential appears through a multiplicative term that is equal to the inverse of its Hessian and which can be interpreted as defining a gradient flow over an appropriately defined Riemannian manifold. We provide numerical simulations which allow us to study and characterize the effect of the mirror potential on the performance of networks trained with SMD for some binary classification problems.
Thompson Sampling Achieves $\tilde O$ Regret in Linear Quadratic Control
Jun 17, 2022
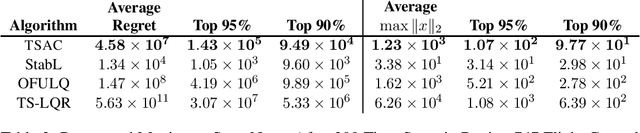

Abstract:Thompson Sampling (TS) is an efficient method for decision-making under uncertainty, where an action is sampled from a carefully prescribed distribution which is updated based on the observed data. In this work, we study the problem of adaptive control of stabilizable linear-quadratic regulators (LQRs) using TS, where the system dynamics are unknown. Previous works have established that $\tilde O(\sqrt{T})$ frequentist regret is optimal for the adaptive control of LQRs. However, the existing methods either work only in restrictive settings, require a priori known stabilizing controllers, or utilize computationally intractable approaches. We propose an efficient TS algorithm for the adaptive control of LQRs, TS-based Adaptive Control, TSAC, that attains $\tilde O(\sqrt{T})$ regret, even for multidimensional systems, thereby solving the open problem posed in Abeille and Lazaric (2018). TSAC does not require a priori known stabilizing controller and achieves fast stabilization of the underlying system by effectively exploring the environment in the early stages. Our result hinges on developing a novel lower bound on the probability that the TS provides an optimistic sample. By carefully prescribing an early exploration strategy and a policy update rule, we show that TS achieves order-optimal regret in adaptive control of multidimensional stabilizable LQRs. We empirically demonstrate the performance and the efficiency of TSAC in several adaptive control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge