Distributionally Robust Kalman Filtering over Finite and Infinite Horizon

This paper investigates the distributionally robust filtering of signals generated by state-space models driven by exogenous disturbances with noisy observations in finite and infinite horizon scenarios. The exact joint probability distribution of the disturbances and noise is unknown but assumed to reside within a Wasserstein-2 ambiguity ball centered around a given nominal distribution. We aim to derive a causal estimator that minimizes the worst-case mean squared estimation error among all possible distributions within this ambiguity set. We remove the iid restriction in prior works by permitting arbitrarily time-correlated disturbances and noises. In the finite horizon setting, we reduce this problem to a semi-definite program (SDP), with computational complexity scaling with the time horizon. For infinite horizon settings, we characterize the optimal estimator using Karush-Kuhn-Tucker (KKT) conditions. Although the optimal estimator lacks a rational form, i.e., a finite-dimensional state-space realization, it can be fully described by a finite-dimensional parameter. {Leveraging this parametrization, we propose efficient algorithms that compute the optimal estimator with arbitrary fidelity in the frequency domain.} Moreover, given any finite degree, we provide an efficient convex optimization algorithm that finds the finite-dimensional state-space estimator that best approximates the optimal non-rational filter in ${\cal H}_\infty$ norm. This facilitates the practical implementation of the infinite horizon filter without having to grapple with the ill-scaled SDP from finite time. Finally, numerical simulations demonstrate the effectiveness of our approach in practical scenarios.

Stochastic Mirror Descent in Average Ensemble Models

The stochastic mirror descent (SMD) algorithm is a general class of training algorithms, which includes the celebrated stochastic gradient descent (SGD), as a special case. It utilizes a mirror potential to influence the implicit bias of the training algorithm. In this paper we explore the performance of the SMD iterates on mean-field ensemble models. Our results generalize earlier ones obtained for SGD on such models. The evolution of the distribution of parameters is mapped to a continuous time process in the space of probability distributions. Our main result gives a nonlinear partial differential equation to which the continuous time process converges in the asymptotic regime of large networks. The impact of the mirror potential appears through a multiplicative term that is equal to the inverse of its Hessian and which can be interpreted as defining a gradient flow over an appropriately defined Riemannian manifold. We provide numerical simulations which allow us to study and characterize the effect of the mirror potential on the performance of networks trained with SMD for some binary classification problems.

Thompson Sampling Achieves $\tilde O$ Regret in Linear Quadratic Control

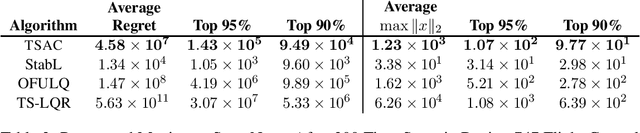
Thompson Sampling (TS) is an efficient method for decision-making under uncertainty, where an action is sampled from a carefully prescribed distribution which is updated based on the observed data. In this work, we study the problem of adaptive control of stabilizable linear-quadratic regulators (LQRs) using TS, where the system dynamics are unknown. Previous works have established that $\tilde O(\sqrt{T})$ frequentist regret is optimal for the adaptive control of LQRs. However, the existing methods either work only in restrictive settings, require a priori known stabilizing controllers, or utilize computationally intractable approaches. We propose an efficient TS algorithm for the adaptive control of LQRs, TS-based Adaptive Control, TSAC, that attains $\tilde O(\sqrt{T})$ regret, even for multidimensional systems, thereby solving the open problem posed in Abeille and Lazaric (2018). TSAC does not require a priori known stabilizing controller and achieves fast stabilization of the underlying system by effectively exploring the environment in the early stages. Our result hinges on developing a novel lower bound on the probability that the TS provides an optimistic sample. By carefully prescribing an early exploration strategy and a policy update rule, we show that TS achieves order-optimal regret in adaptive control of multidimensional stabilizable LQRs. We empirically demonstrate the performance and the efficiency of TSAC in several adaptive control tasks.