EKGNet: A 10.96μW Fully Analog Neural Network for Intra-Patient Arrhythmia Classification

We present an integrated approach by combining analog computing and deep learning for electrocardiogram (ECG) arrhythmia classification. We propose EKGNet, a hardware-efficient and fully analog arrhythmia classification architecture that archives high accuracy with low power consumption. The proposed architecture leverages the energy efficiency of transistors operating in the subthreshold region, eliminating the need for analog-to-digital converters (ADC) and static random access memory (SRAM). The system design includes a novel analog sequential Multiply-Accumulate (MAC) circuit that mitigates process, supply voltage, and temperature variations. Experimental evaluations on PhysioNet's MIT-BIH and PTB Diagnostics datasets demonstrate the effectiveness of the proposed method, achieving average balanced accuracy of 95% and 94.25% for intra-patient arrhythmia classification and myocardial infarction (MI) classification, respectively. This innovative approach presents a promising avenue for developing low-power arrhythmia classification systems with enhanced accuracy and transferability in biomedical applications.

Forecasting subcritical cylinder wakes with Fourier Neural Operators

We apply Fourier neural operators (FNOs), a state-of-the-art operator learning technique, to forecast the temporal evolution of experimentally measured velocity fields. FNOs are a recently developed machine learning method capable of approximating solution operators to systems of partial differential equations through data alone. The learned FNO solution operator can be evaluated in milliseconds, potentially enabling faster-than-real-time modeling for predictive flow control in physical systems. Here we use FNOs to predict how physical fluid flows evolve in time, training with particle image velocimetry measurements depicting cylinder wakes in the subcritical vortex shedding regime. We train separate FNOs at Reynolds numbers ranging from Re = 240 to Re = 3060 and study how increasingly turbulent flow phenomena impact prediction accuracy. We focus here on a short prediction horizon of ten non-dimensionalized time-steps, as would be relevant for problems of predictive flow control. We find that FNOs are capable of accurately predicting the evolution of experimental velocity fields throughout the range of Reynolds numbers tested (L2 norm error < 0.1) despite being provided with limited and imperfect flow observations. Given these results, we conclude that this method holds significant potential for real-time predictive flow control of physical systems.

Thompson Sampling Achieves $\tilde O$ Regret in Linear Quadratic Control

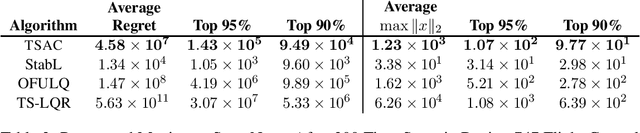
Thompson Sampling (TS) is an efficient method for decision-making under uncertainty, where an action is sampled from a carefully prescribed distribution which is updated based on the observed data. In this work, we study the problem of adaptive control of stabilizable linear-quadratic regulators (LQRs) using TS, where the system dynamics are unknown. Previous works have established that $\tilde O(\sqrt{T})$ frequentist regret is optimal for the adaptive control of LQRs. However, the existing methods either work only in restrictive settings, require a priori known stabilizing controllers, or utilize computationally intractable approaches. We propose an efficient TS algorithm for the adaptive control of LQRs, TS-based Adaptive Control, TSAC, that attains $\tilde O(\sqrt{T})$ regret, even for multidimensional systems, thereby solving the open problem posed in Abeille and Lazaric (2018). TSAC does not require a priori known stabilizing controller and achieves fast stabilization of the underlying system by effectively exploring the environment in the early stages. Our result hinges on developing a novel lower bound on the probability that the TS provides an optimistic sample. By carefully prescribing an early exploration strategy and a policy update rule, we show that TS achieves order-optimal regret in adaptive control of multidimensional stabilizable LQRs. We empirically demonstrate the performance and the efficiency of TSAC in several adaptive control tasks.

Optimal Competitive-Ratio Control

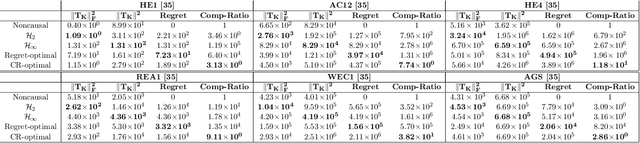
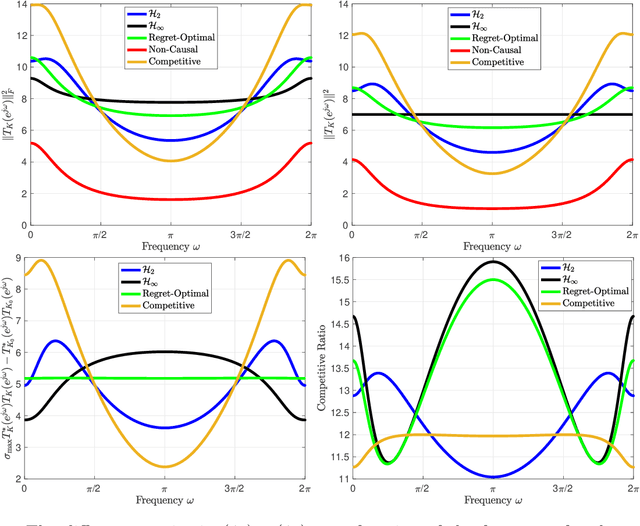
Inspired by competitive policy designs approaches in online learning, new control paradigms such as competitive-ratio and regret-optimal control have been recently proposed as alternatives to the classical $\mathcal{H}_2$ and $\mathcal{H}_\infty$ approaches. These competitive metrics compare the control cost of the designed controller against the cost of a clairvoyant controller, which has access to past, present, and future disturbances in terms of ratio and difference, respectively. While prior work provided the optimal solution for the regret-optimal control problem, in competitive-ratio control, the solution is only provided for the sub-optimal problem. In this work, we derive the optimal solution to the competitive-ratio control problem. We show that the optimal competitive ratio formula can be computed as the maximal eigenvalue of a simple matrix, and provide a state-space controller that achieves the optimal competitive ratio. We conduct an extensive numerical study to verify this analytical solution, and demonstrate that the optimal competitive-ratio controller outperforms other controllers on several large scale practical systems. The key techniques that underpin our explicit solution is a reduction of the control problem to a Nehari problem, along with a novel factorization of the clairvoyant controller's cost. We reveal an interesting relation between the explicit solutions that now exist for both competitive control paradigms by formulating a regret-optimal control framework with weight functions that can also be utilized for practical purposes.

KCRL: Krasovskii-Constrained Reinforcement Learning with Guaranteed Stability in Nonlinear Dynamical Systems

Learning a dynamical system requires stabilizing the unknown dynamics to avoid state blow-ups. However, current reinforcement learning (RL) methods lack stabilization guarantees, which limits their applicability for the control of safety-critical systems. We propose a model-based RL framework with formal stability guarantees, Krasovskii Constrained RL (KCRL), that adopts Krasovskii's family of Lyapunov functions as a stability constraint. The proposed method learns the system dynamics up to a confidence interval using feature representation, e.g. Random Fourier Features. It then solves a constrained policy optimization problem with a stability constraint based on Krasovskii's method using a primal-dual approach to recover a stabilizing policy. We show that KCRL is guaranteed to learn a stabilizing policy in a finite number of interactions with the underlying unknown system. We also derive the sample complexity upper bound for stabilization of unknown nonlinear dynamical systems via the KCRL framework.

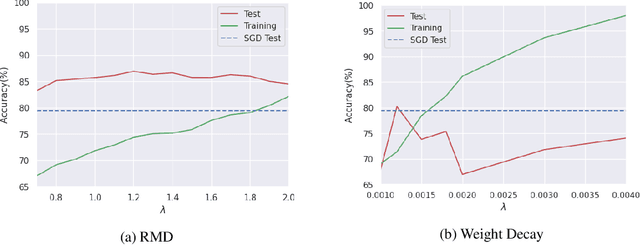
Explicit Regularization via Regularizer Mirror Descent

Despite perfectly interpolating the training data, deep neural networks (DNNs) can often generalize fairly well, in part due to the "implicit regularization" induced by the learning algorithm. Nonetheless, various forms of regularization, such as "explicit regularization" (via weight decay), are often used to avoid overfitting, especially when the data is corrupted. There are several challenges with explicit regularization, most notably unclear convergence properties. Inspired by convergence properties of stochastic mirror descent (SMD) algorithms, we propose a new method for training DNNs with regularization, called regularizer mirror descent (RMD). In highly overparameterized DNNs, SMD simultaneously interpolates the training data and minimizes a certain potential function of the weights. RMD starts with a standard cost which is the sum of the training loss and a convex regularizer of the weights. Reinterpreting this cost as the potential of an "augmented" overparameterized network and applying SMD yields RMD. As a result, RMD inherits the properties of SMD and provably converges to a point "close" to the minimizer of this cost. RMD is computationally comparable to stochastic gradient descent (SGD) and weight decay, and is parallelizable in the same manner. Our experimental results on training sets with various levels of corruption suggest that the generalization performance of RMD is remarkably robust and significantly better than both SGD and weight decay, which implicitly and explicitly regularize the $\ell_2$ norm of the weights. RMD can also be used to regularize the weights to a desired weight vector, which is particularly relevant for continual learning.

CEM-GD: Cross-Entropy Method with Gradient Descent Planner for Model-Based Reinforcement Learning

Current state-of-the-art model-based reinforcement learning algorithms use trajectory sampling methods, such as the Cross-Entropy Method (CEM), for planning in continuous control settings. These zeroth-order optimizers require sampling a large number of trajectory rollouts to select an optimal action, which scales poorly for large prediction horizons or high dimensional action spaces. First-order methods that use the gradients of the rewards with respect to the actions as an update can mitigate this issue, but suffer from local optima due to the non-convex optimization landscape. To overcome these issues and achieve the best of both worlds, we propose a novel planner, Cross-Entropy Method with Gradient Descent (CEM-GD), that combines first-order methods with CEM. At the beginning of execution, CEM-GD uses CEM to sample a significant amount of trajectory rollouts to explore the optimization landscape and avoid poor local minima. It then uses the top trajectories as initialization for gradient descent and applies gradient updates to each of these trajectories to find the optimal action sequence. At each subsequent time step, however, CEM-GD samples much fewer trajectories from CEM before applying gradient updates. We show that as the dimensionality of the planning problem increases, CEM-GD maintains desirable performance with a constant small number of samples by using the gradient information, while avoiding local optima using initially well-sampled trajectories. Furthermore, CEM-GD achieves better performance than CEM on a variety of continuous control benchmarks in MuJoCo with 100x fewer samples per time step, resulting in around 25% less computation time and 10% less memory usage. The implementation of CEM-GD is available at $\href{https://github.com/KevinHuang8/CEM-GD}{\text{https://github.com/KevinHuang8/CEM-GD}}$.

Finite-time System Identification and Adaptive Control in Autoregressive Exogenous Systems

Autoregressive exogenous (ARX) systems are the general class of input-output dynamical systems used for modeling stochastic linear dynamical systems (LDS) including partially observable LDS such as LQG systems. In this work, we study the problem of system identification and adaptive control of unknown ARX systems. We provide finite-time learning guarantees for the ARX systems under both open-loop and closed-loop data collection. Using these guarantees, we design adaptive control algorithms for unknown ARX systems with arbitrary strongly convex or convex quadratic regulating costs. Under strongly convex cost functions, we design an adaptive control algorithm based on online gradient descent to design and update the controllers that are constructed via a convex controller reparametrization. We show that our algorithm has $\tilde{\mathcal{O}}(\sqrt{T})$ regret via explore and commit approach and if the model estimates are updated in epochs using closed-loop data collection, it attains the optimal regret of $\text{polylog}(T)$ after $T$ time-steps of interaction. For the case of convex quadratic cost functions, we propose an adaptive control algorithm that deploys the optimism in the face of uncertainty principle to design the controller. In this setting, we show that the explore and commit approach has a regret upper bound of $\tilde{\mathcal{O}}(T^{2/3})$, and the adaptive control with continuous model estimate updates attains $\tilde{\mathcal{O}}(\sqrt{T})$ regret after $T$ time-steps.

Regret-Optimal Full-Information Control

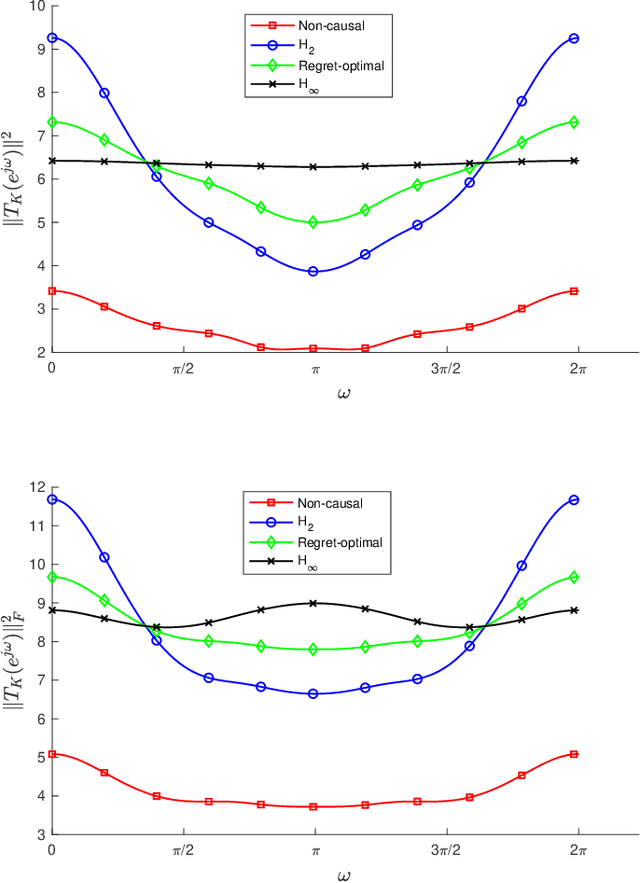
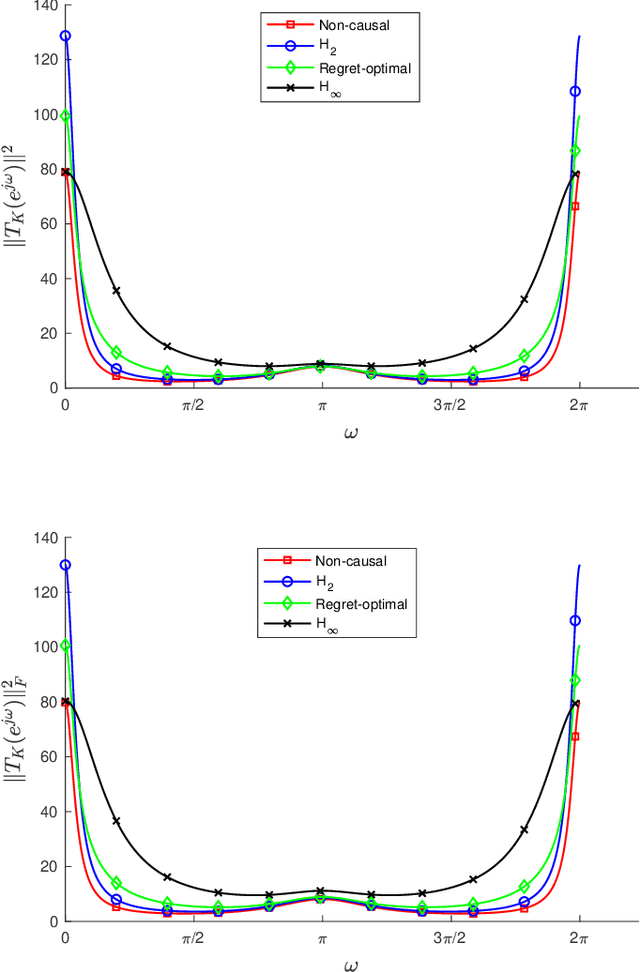
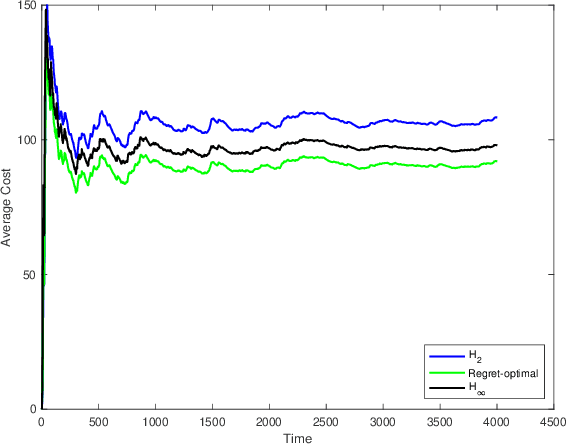
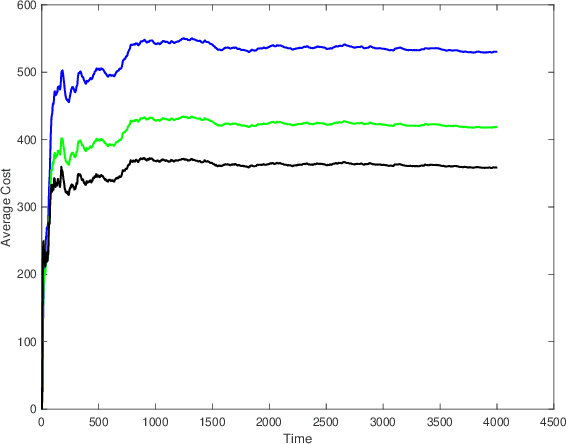
We consider the infinite-horizon, discrete-time full-information control problem. Motivated by learning theory, as a criterion for controller design we focus on regret, defined as the difference between the LQR cost of a causal controller (that has only access to past and current disturbances) and the LQR cost of a clairvoyant one (that has also access to future disturbances). In the full-information setting, there is a unique optimal non-causal controller that in terms of LQR cost dominates all other controllers. Since the regret itself is a function of the disturbances, we consider the worst-case regret over all possible bounded energy disturbances, and propose to find a causal controller that minimizes this worst-case regret. The resulting controller has the interpretation of guaranteeing the smallest possible regret compared to the best non-causal controller, no matter what the future disturbances are. We show that the regret-optimal control problem can be reduced to a Nehari problem, i.e., to approximate an anticausal operator with a causal one in the operator norm. In the state-space setting, explicit formulas for the optimal regret and for the regret-optimal controller (in both the causal and the strictly causal settings) are derived. The regret-optimal controller is the sum of the classical $H_2$ state-feedback law and a finite-dimensional controller obtained from the Nehari problem. The controller construction simply requires the solution to the standard LQR Riccati equation, in addition to two Lyapunov equations. Simulations over a range of plants demonstrates that the regret-optimal controller interpolates nicely between the $H_2$ and the $H_\infty$ optimal controllers, and generally has $H_2$ and $H_\infty$ costs that are simultaneously close to their optimal values. The regret-optimal controller thus presents itself as a viable option for control system design.

Stable Online Control of Linear Time-Varying Systems

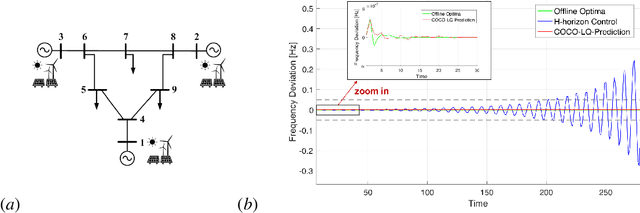
Linear time-varying (LTV) systems are widely used for modeling real-world dynamical systems due to their generality and simplicity. Providing stability guarantees for LTV systems is one of the central problems in control theory. However, existing approaches that guarantee stability typically lead to significantly sub-optimal cumulative control cost in online settings where only current or short-term system information is available. In this work, we propose an efficient online control algorithm, COvariance Constrained Online Linear Quadratic (COCO-LQ) control, that guarantees input-to-state stability for a large class of LTV systems while also minimizing the control cost. The proposed method incorporates a state covariance constraint into the semi-definite programming (SDP) formulation of the LQ optimal controller. We empirically demonstrate the performance of COCO-LQ in both synthetic experiments and a power system frequency control example.