Optimal Competitive-Ratio Control

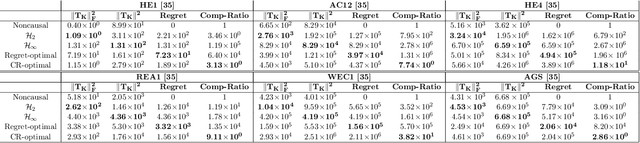
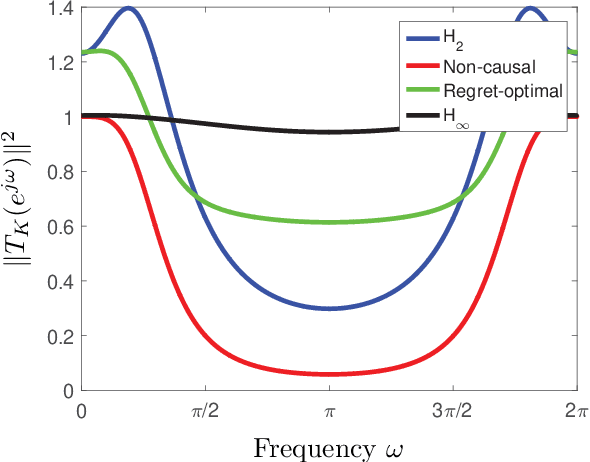
Inspired by competitive policy designs approaches in online learning, new control paradigms such as competitive-ratio and regret-optimal control have been recently proposed as alternatives to the classical $\mathcal{H}_2$ and $\mathcal{H}_\infty$ approaches. These competitive metrics compare the control cost of the designed controller against the cost of a clairvoyant controller, which has access to past, present, and future disturbances in terms of ratio and difference, respectively. While prior work provided the optimal solution for the regret-optimal control problem, in competitive-ratio control, the solution is only provided for the sub-optimal problem. In this work, we derive the optimal solution to the competitive-ratio control problem. We show that the optimal competitive ratio formula can be computed as the maximal eigenvalue of a simple matrix, and provide a state-space controller that achieves the optimal competitive ratio. We conduct an extensive numerical study to verify this analytical solution, and demonstrate that the optimal competitive-ratio controller outperforms other controllers on several large scale practical systems. The key techniques that underpin our explicit solution is a reduction of the control problem to a Nehari problem, along with a novel factorization of the clairvoyant controller's cost. We reveal an interesting relation between the explicit solutions that now exist for both competitive control paradigms by formulating a regret-optimal control framework with weight functions that can also be utilized for practical purposes.

Regret-Optimal Full-Information Control

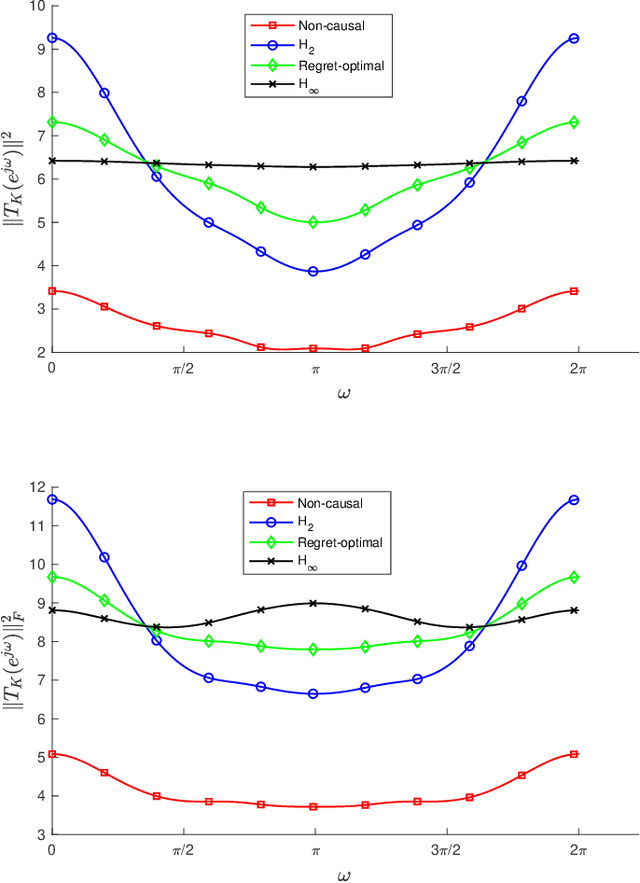
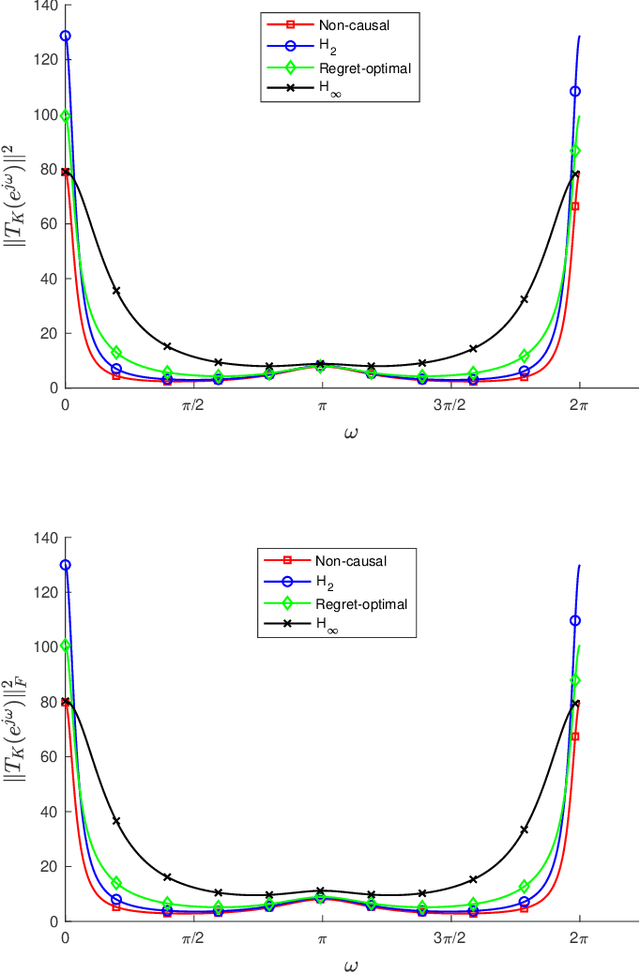
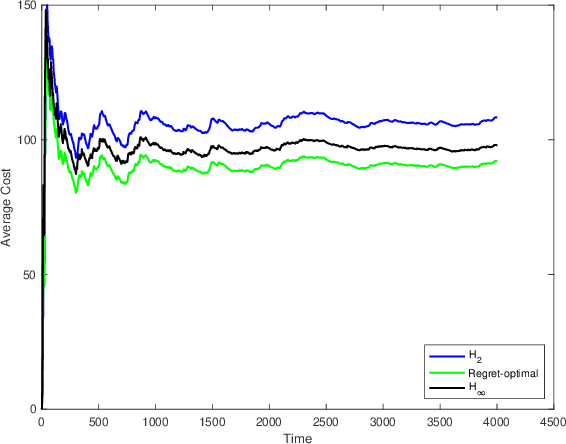
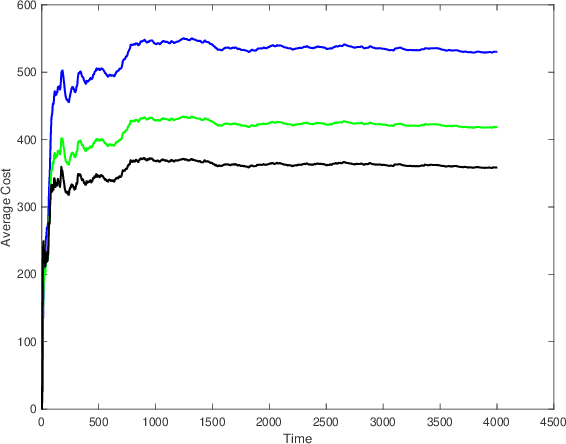
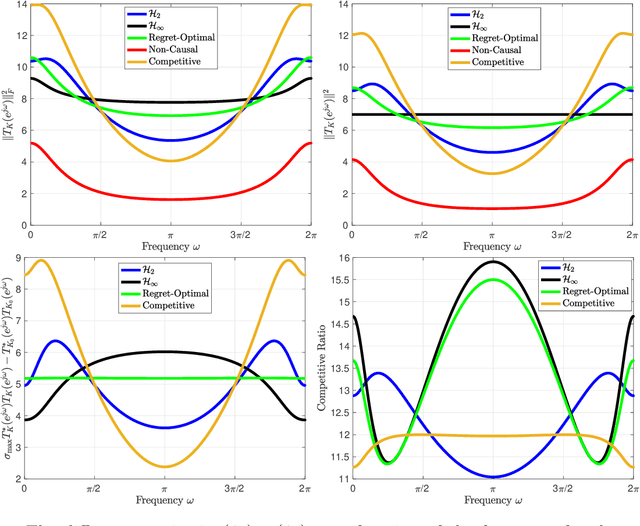
We consider the infinite-horizon, discrete-time full-information control problem. Motivated by learning theory, as a criterion for controller design we focus on regret, defined as the difference between the LQR cost of a causal controller (that has only access to past and current disturbances) and the LQR cost of a clairvoyant one (that has also access to future disturbances). In the full-information setting, there is a unique optimal non-causal controller that in terms of LQR cost dominates all other controllers. Since the regret itself is a function of the disturbances, we consider the worst-case regret over all possible bounded energy disturbances, and propose to find a causal controller that minimizes this worst-case regret. The resulting controller has the interpretation of guaranteeing the smallest possible regret compared to the best non-causal controller, no matter what the future disturbances are. We show that the regret-optimal control problem can be reduced to a Nehari problem, i.e., to approximate an anticausal operator with a causal one in the operator norm. In the state-space setting, explicit formulas for the optimal regret and for the regret-optimal controller (in both the causal and the strictly causal settings) are derived. The regret-optimal controller is the sum of the classical $H_2$ state-feedback law and a finite-dimensional controller obtained from the Nehari problem. The controller construction simply requires the solution to the standard LQR Riccati equation, in addition to two Lyapunov equations. Simulations over a range of plants demonstrates that the regret-optimal controller interpolates nicely between the $H_2$ and the $H_\infty$ optimal controllers, and generally has $H_2$ and $H_\infty$ costs that are simultaneously close to their optimal values. The regret-optimal controller thus presents itself as a viable option for control system design.

Regret-Optimal Filtering

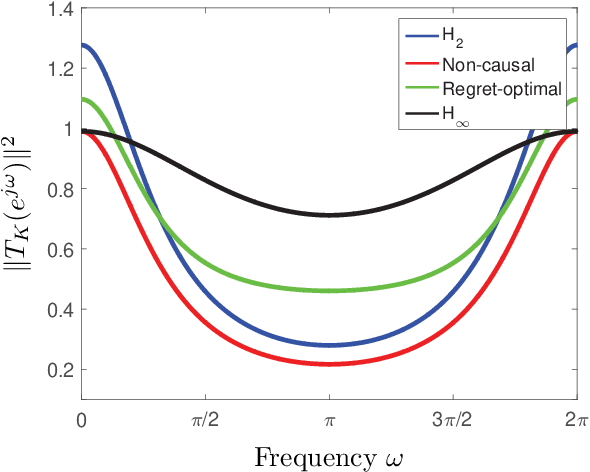
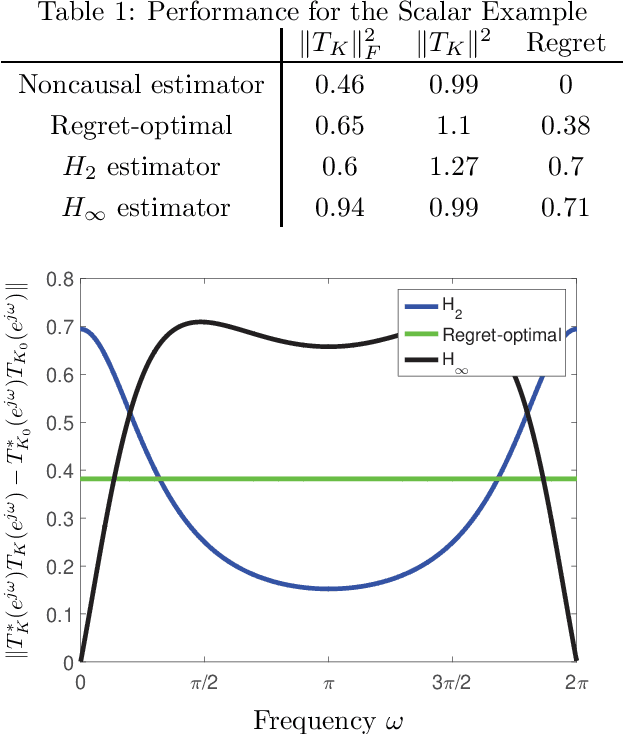
We consider the problem of filtering in linear state-space models (e.g., the Kalman filter setting) through the lens of regret optimization. Different assumptions on the driving disturbance and the observation noise sequences give rise to different estimators: in the stochastic setting to the celebrated Kalman filter, and in the deterministic setting of bounded energy disturbances to $H_\infty$ estimators. In this work, we formulate a novel criterion for filter design based on the concept of regret between the estimation error energy of a clairvoyant estimator that has access to all future observations (a so-called smoother) and a causal one that only has access to current and past observations. The regret-optimal estimator is chosen to minimize this worst-case difference across all bounded-energy noise sequences. The resulting estimator is adaptive in the sense that it aims to mimic the behavior of the clairvoyant estimator, irrespective of what the realization of the noise will be and thus interpolates between the stochastic and deterministic approaches. We provide a solution for the regret estimation problem at two different levels. First, we provide a solution at the operator level by reducing it to the Nehari problem. Second, for state-space models, we explicitly find the estimator that achieves the optimal regret. From a computational perspective, the regret-optimal estimator can be easily implemented by solving three Riccati equations and a single Lyapunov equation. For a state-space model of dimension $n$, the regret-optimal estimator has a state-space structure of dimension $3n$. We demonstrate the applicability and efficacy of the estimator in a variety of problems and observe that the estimator has average and worst-case performances that are simultaneously close to their optimal values. We therefore argue that regret-optimality is a viable approach to estimator design.

Computing the Feedback Capacity of Finite State Channels using Reinforcement Learning

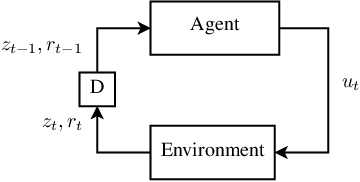
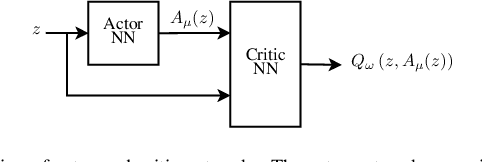
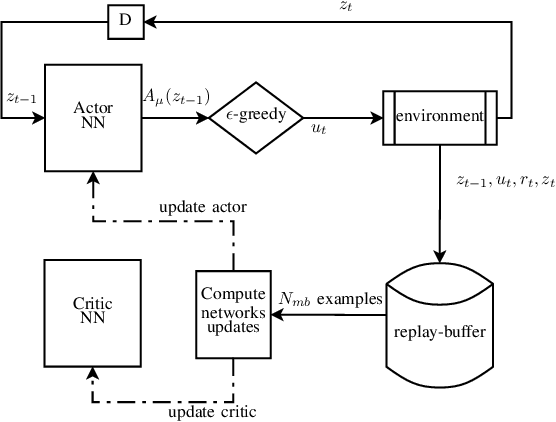
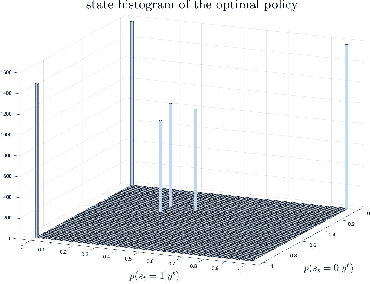
In this paper, we propose a novel method to compute the feedback capacity of channels with memory using reinforcement learning (RL). In RL, one seeks to maximize cumulative rewards collected in a sequential decision-making environment. This is done by collecting samples of the underlying environment and using them to learn the optimal decision rule. The main advantage of this approach is its computational efficiency, even in high dimensional problems. Hence, RL can be used to estimate numerically the feedback capacity of unifilar finite state channels (FSCs) with large alphabet size. The outcome of the RL algorithm sheds light on the properties of the optimal decision rule, which in our case, is the optimal input distribution of the channel. These insights can be converted into analytic, single-letter capacity expressions by solving corresponding lower and upper bounds. We demonstrate the efficiency of this method by analytically solving the feedback capacity of the well-known Ising channel with a ternary alphabet. We also provide a simple coding scheme that achieves the feedback capacity.