Regret-Optimal Full-Information Control

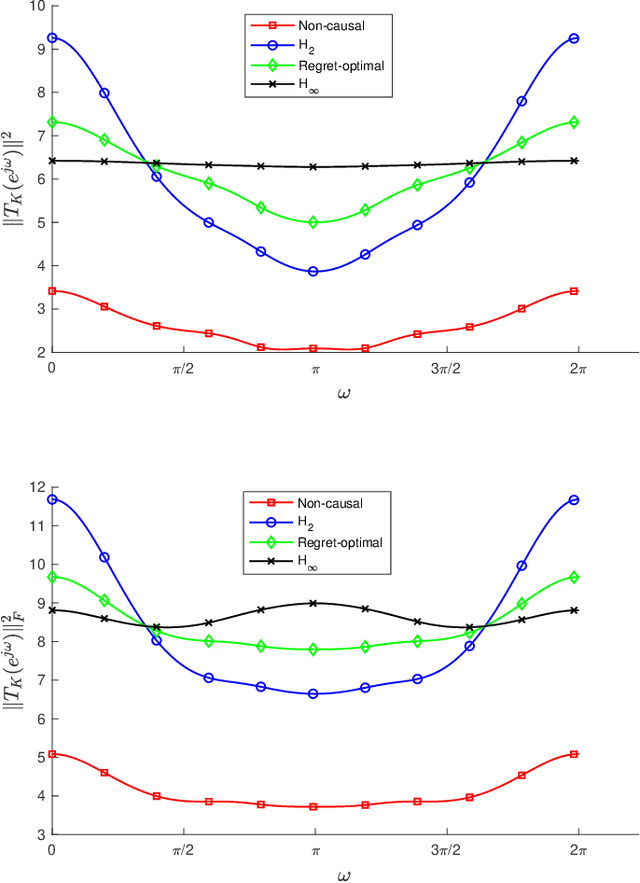
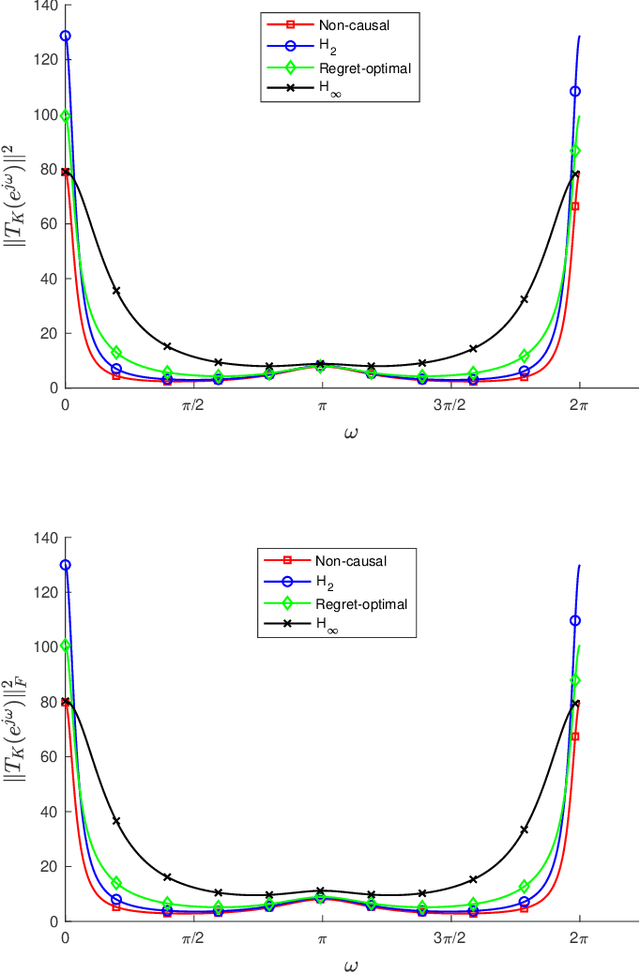
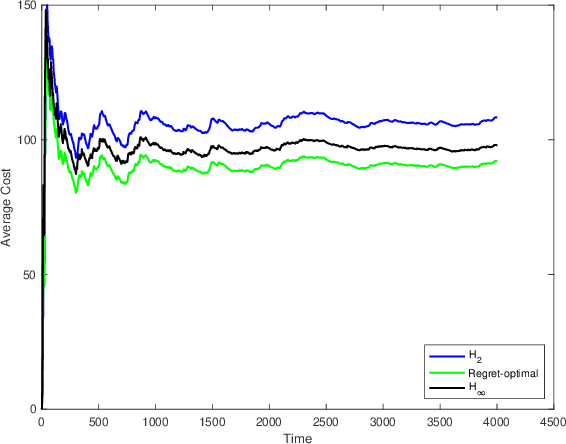
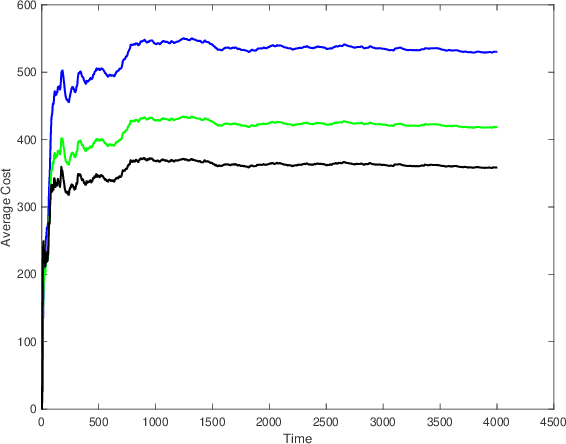
We consider the infinite-horizon, discrete-time full-information control problem. Motivated by learning theory, as a criterion for controller design we focus on regret, defined as the difference between the LQR cost of a causal controller (that has only access to past and current disturbances) and the LQR cost of a clairvoyant one (that has also access to future disturbances). In the full-information setting, there is a unique optimal non-causal controller that in terms of LQR cost dominates all other controllers. Since the regret itself is a function of the disturbances, we consider the worst-case regret over all possible bounded energy disturbances, and propose to find a causal controller that minimizes this worst-case regret. The resulting controller has the interpretation of guaranteeing the smallest possible regret compared to the best non-causal controller, no matter what the future disturbances are. We show that the regret-optimal control problem can be reduced to a Nehari problem, i.e., to approximate an anticausal operator with a causal one in the operator norm. In the state-space setting, explicit formulas for the optimal regret and for the regret-optimal controller (in both the causal and the strictly causal settings) are derived. The regret-optimal controller is the sum of the classical $H_2$ state-feedback law and a finite-dimensional controller obtained from the Nehari problem. The controller construction simply requires the solution to the standard LQR Riccati equation, in addition to two Lyapunov equations. Simulations over a range of plants demonstrates that the regret-optimal controller interpolates nicely between the $H_2$ and the $H_\infty$ optimal controllers, and generally has $H_2$ and $H_\infty$ costs that are simultaneously close to their optimal values. The regret-optimal controller thus presents itself as a viable option for control system design.