Stochastic Mirror Descent in Average Ensemble Models

The stochastic mirror descent (SMD) algorithm is a general class of training algorithms, which includes the celebrated stochastic gradient descent (SGD), as a special case. It utilizes a mirror potential to influence the implicit bias of the training algorithm. In this paper we explore the performance of the SMD iterates on mean-field ensemble models. Our results generalize earlier ones obtained for SGD on such models. The evolution of the distribution of parameters is mapped to a continuous time process in the space of probability distributions. Our main result gives a nonlinear partial differential equation to which the continuous time process converges in the asymptotic regime of large networks. The impact of the mirror potential appears through a multiplicative term that is equal to the inverse of its Hessian and which can be interpreted as defining a gradient flow over an appropriately defined Riemannian manifold. We provide numerical simulations which allow us to study and characterize the effect of the mirror potential on the performance of networks trained with SMD for some binary classification problems.

Robustifying Binary Classification to Adversarial Perturbation

Despite the enormous success of machine learning models in various applications, most of these models lack resilience to (even small) perturbations in their input data. Hence, new methods to robustify machine learning models seem very essential. To this end, in this paper we consider the problem of binary classification with adversarial perturbations. Investigating the solution to a min-max optimization (which considers the worst-case loss in the presence of adversarial perturbations) we introduce a generalization to the max-margin classifier which takes into account the power of the adversary in manipulating the data. We refer to this classifier as the "Robust Max-margin" (RM) classifier. Under some mild assumptions on the loss function, we theoretically show that the gradient descent iterates (with sufficiently small step size) converge to the RM classifier in its direction. Therefore, the RM classifier can be studied to compute various performance measures (e.g. generalization error) of binary classification with adversarial perturbations.

The Performance Analysis of Generalized Margin Maximizer (GMM) on Separable Data

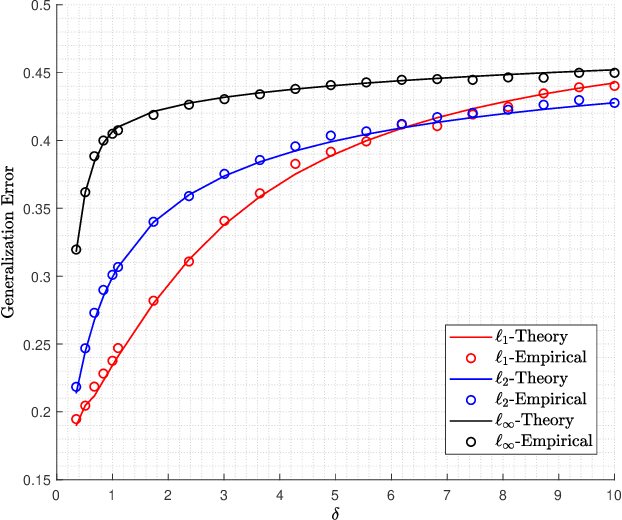
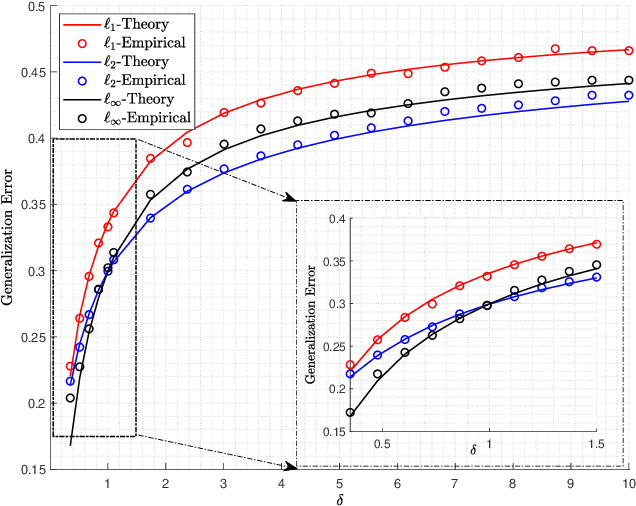
Logistic models are commonly used for binary classification tasks. The success of such models has often been attributed to their connection to maximum-likelihood estimators. It has been shown that gradient descent algorithm, when applied on the logistic loss, converges to the max-margin classifier (a.k.a. hard-margin SVM). The performance of the max-margin classifier has been recently analyzed. Inspired by these results, in this paper, we present and study a more general setting, where the underlying parameters of the logistic model possess certain structures (sparse, block-sparse, low-rank, etc.) and introduce a more general framework (which is referred to as "Generalized Margin Maximizer", GMM). While classical max-margin classifiers minimize the $2$-norm of the parameter vector subject to linearly separating the data, GMM minimizes any arbitrary convex function of the parameter vector. We provide a precise analysis of the performance of GMM via the solution of a system of nonlinear equations. We also provide a detailed study for three special cases: ($1$) $\ell_2$-GMM that is the max-margin classifier, ($2$) $\ell_1$-GMM which encourages sparsity, and ($3$) $\ell_{\infty}$-GMM which is often used when the parameter vector has binary entries. Our theoretical results are validated by extensive simulation results across a range of parameter values, problem instances, and model structures.

Federated Learning with Autotuned Communication-Efficient Secure Aggregation

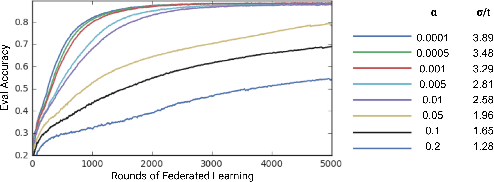
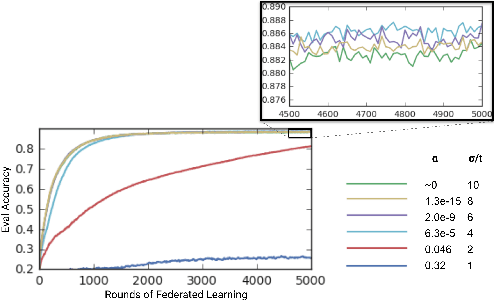
Federated Learning enables mobile devices to collaboratively learn a shared inference model while keeping all the training data on a user's device, decoupling the ability to do machine learning from the need to store the data in the cloud. Existing work on federated learning with limited communication demonstrates how random rotation can enable users' model updates to be quantized much more efficiently, reducing the communication cost between users and the server. Meanwhile, secure aggregation enables the server to learn an aggregate of at least a threshold number of device's model contributions without observing any individual device's contribution in unaggregated form. In this paper, we highlight some of the challenges of setting the parameters for secure aggregation to achieve communication efficiency, especially in the context of the aggressively quantized inputs enabled by random rotation. We then develop a recipe for auto-tuning communication-efficient secure aggregation, based on specific properties of random rotation and secure aggregation -- namely, the predictable distribution of vector entries post-rotation and the modular wrapping inherent in secure aggregation. We present both theoretical results and initial experiments.

The Impact of Regularization on High-dimensional Logistic Regression

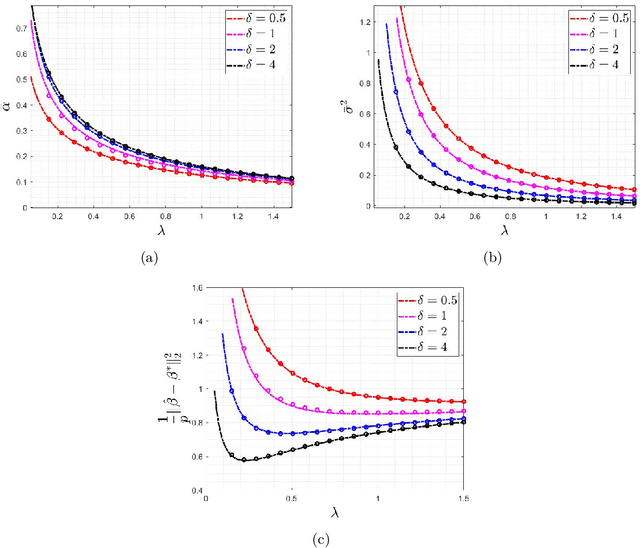
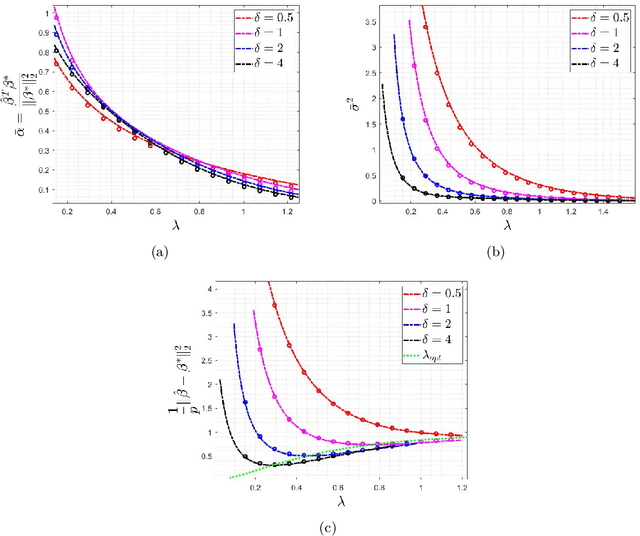
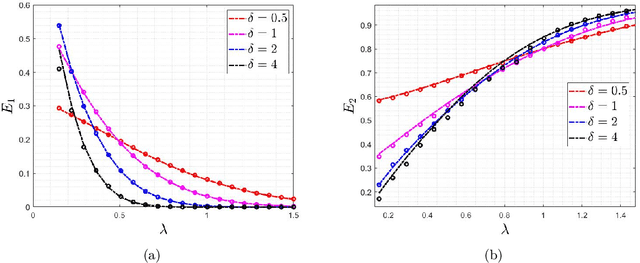
Logistic regression is commonly used for modeling dichotomous outcomes. In the classical setting, where the number of observations is much larger than the number of parameters, properties of the maximum likelihood estimator in logistic regression are well understood. Recently, Sur and Candes have studied logistic regression in the high-dimensional regime, where the number of observations and parameters are comparable, and show, among other things, that the maximum likelihood estimator is biased. In the high-dimensional regime the underlying parameter vector is often structured (sparse, block-sparse, finite-alphabet, etc.) and so in this paper we study regularized logistic regression (RLR), where a convex regularizer that encourages the desired structure is added to the negative of the log-likelihood function. An advantage of RLR is that it allows parameter recovery even for instances where the (unconstrained) maximum likelihood estimate does not exist. We provide a precise analysis of the performance of RLR via the solution of a system of six nonlinear equations, through which any performance metric of interest (mean, mean-squared error, probability of support recovery, etc.) can be explicitly computed. Our results generalize those of Sur and Candes and we provide a detailed study for the cases of $\ell_2^2$-RLR and sparse ($\ell_1$-regularized) logistic regression. In both cases, we obtain explicit expressions for various performance metrics and can find the values of the regularizer parameter that optimizes the desired performance. The theory is validated by extensive numerical simulations across a range of parameter values and problem instances.