The Performance Analysis of Generalized Margin Maximizer (GMM) on Separable Data

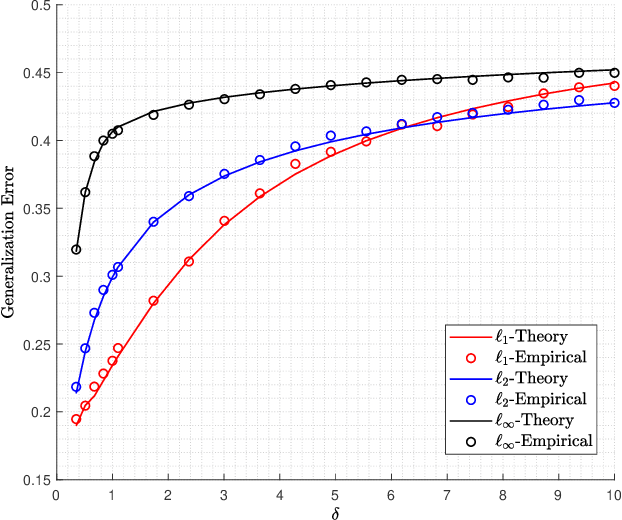
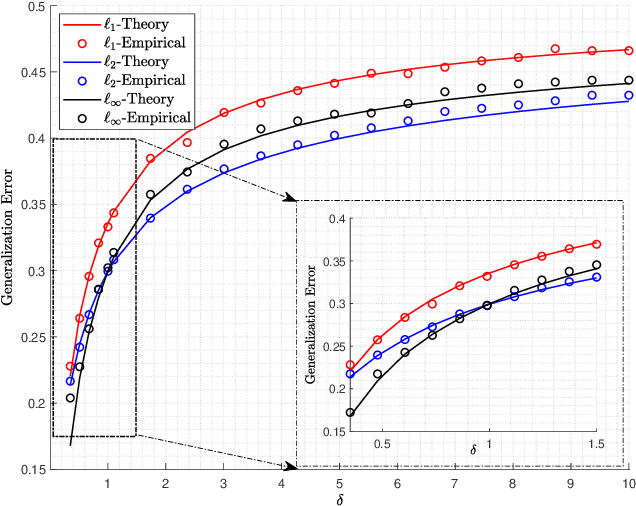
Logistic models are commonly used for binary classification tasks. The success of such models has often been attributed to their connection to maximum-likelihood estimators. It has been shown that gradient descent algorithm, when applied on the logistic loss, converges to the max-margin classifier (a.k.a. hard-margin SVM). The performance of the max-margin classifier has been recently analyzed. Inspired by these results, in this paper, we present and study a more general setting, where the underlying parameters of the logistic model possess certain structures (sparse, block-sparse, low-rank, etc.) and introduce a more general framework (which is referred to as "Generalized Margin Maximizer", GMM). While classical max-margin classifiers minimize the $2$-norm of the parameter vector subject to linearly separating the data, GMM minimizes any arbitrary convex function of the parameter vector. We provide a precise analysis of the performance of GMM via the solution of a system of nonlinear equations. We also provide a detailed study for three special cases: ($1$) $\ell_2$-GMM that is the max-margin classifier, ($2$) $\ell_1$-GMM which encourages sparsity, and ($3$) $\ell_{\infty}$-GMM which is often used when the parameter vector has binary entries. Our theoretical results are validated by extensive simulation results across a range of parameter values, problem instances, and model structures.

The Impact of Regularization on High-dimensional Logistic Regression

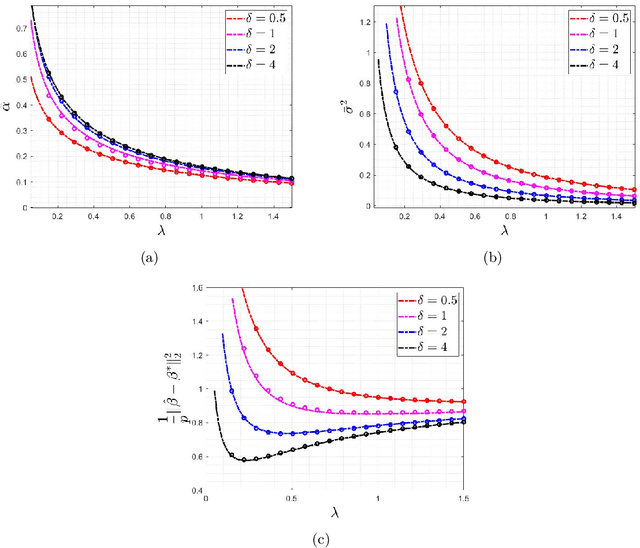
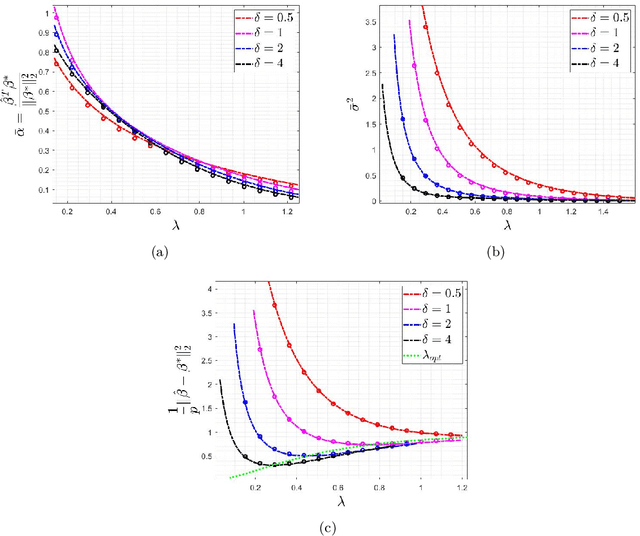
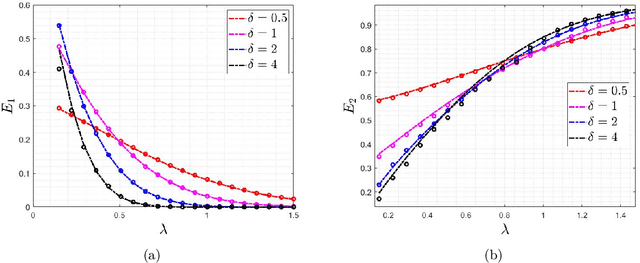
Logistic regression is commonly used for modeling dichotomous outcomes. In the classical setting, where the number of observations is much larger than the number of parameters, properties of the maximum likelihood estimator in logistic regression are well understood. Recently, Sur and Candes have studied logistic regression in the high-dimensional regime, where the number of observations and parameters are comparable, and show, among other things, that the maximum likelihood estimator is biased. In the high-dimensional regime the underlying parameter vector is often structured (sparse, block-sparse, finite-alphabet, etc.) and so in this paper we study regularized logistic regression (RLR), where a convex regularizer that encourages the desired structure is added to the negative of the log-likelihood function. An advantage of RLR is that it allows parameter recovery even for instances where the (unconstrained) maximum likelihood estimate does not exist. We provide a precise analysis of the performance of RLR via the solution of a system of six nonlinear equations, through which any performance metric of interest (mean, mean-squared error, probability of support recovery, etc.) can be explicitly computed. Our results generalize those of Sur and Candes and we provide a detailed study for the cases of $\ell_2^2$-RLR and sparse ($\ell_1$-regularized) logistic regression. In both cases, we obtain explicit expressions for various performance metrics and can find the values of the regularizer parameter that optimizes the desired performance. The theory is validated by extensive numerical simulations across a range of parameter values and problem instances.