The Performance Analysis of Generalized Margin Maximizer (GMM) on Separable Data
Paper and Code
Oct 29, 2020

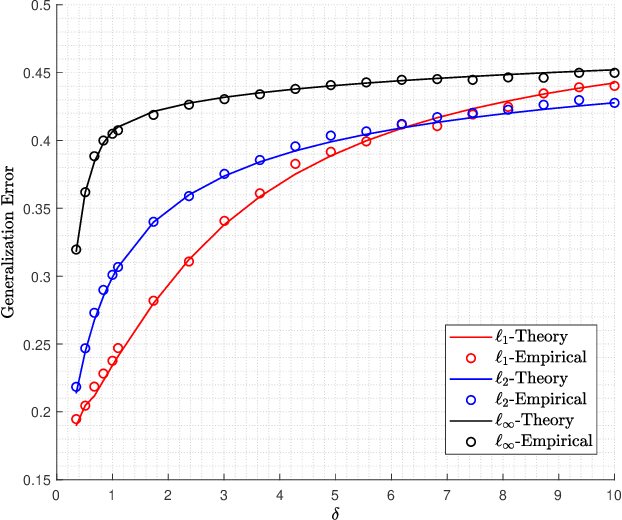
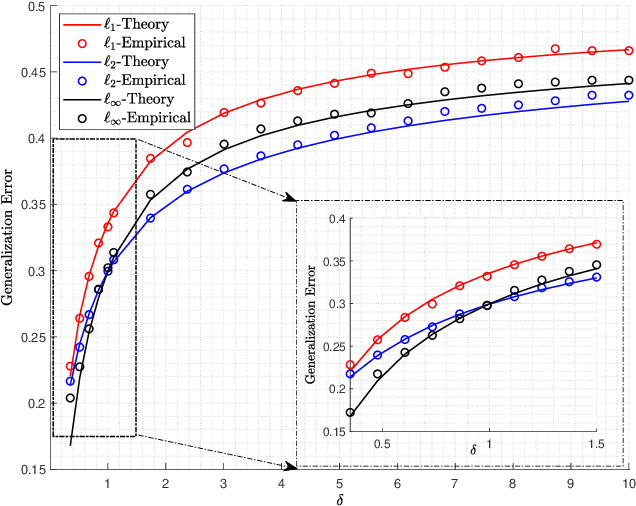
Logistic models are commonly used for binary classification tasks. The success of such models has often been attributed to their connection to maximum-likelihood estimators. It has been shown that gradient descent algorithm, when applied on the logistic loss, converges to the max-margin classifier (a.k.a. hard-margin SVM). The performance of the max-margin classifier has been recently analyzed. Inspired by these results, in this paper, we present and study a more general setting, where the underlying parameters of the logistic model possess certain structures (sparse, block-sparse, low-rank, etc.) and introduce a more general framework (which is referred to as "Generalized Margin Maximizer", GMM). While classical max-margin classifiers minimize the $2$-norm of the parameter vector subject to linearly separating the data, GMM minimizes any arbitrary convex function of the parameter vector. We provide a precise analysis of the performance of GMM via the solution of a system of nonlinear equations. We also provide a detailed study for three special cases: ($1$) $\ell_2$-GMM that is the max-margin classifier, ($2$) $\ell_1$-GMM which encourages sparsity, and ($3$) $\ell_{\infty}$-GMM which is often used when the parameter vector has binary entries. Our theoretical results are validated by extensive simulation results across a range of parameter values, problem instances, and model structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge