A Novel Gaussian Min-Max Theorem and its Applications

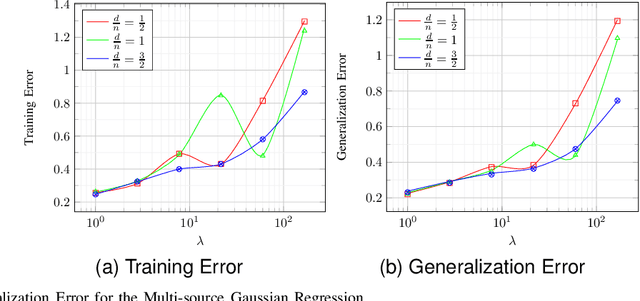
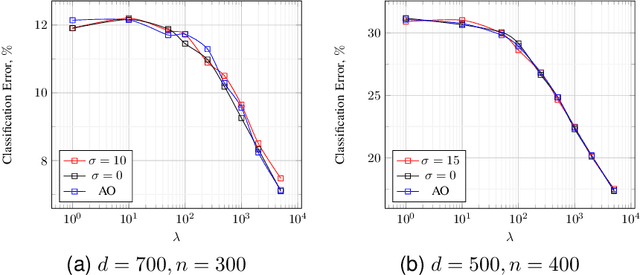
A celebrated result by Gordon allows one to compare the min-max behavior of two Gaussian processes if certain inequality conditions are met. The consequences of this result include the Gaussian min-max (GMT) and convex Gaussian min-max (CGMT) theorems which have had far-reaching implications in high-dimensional statistics, machine learning, non-smooth optimization, and signal processing. Both theorems rely on a pair of Gaussian processes, first identified by Slepian, that satisfy Gordon's comparison inequalities. To date, no other pair of Gaussian processes satisfying these inequalities has been discovered. In this paper, we identify such a new pair. The resulting theorems extend the classical GMT and CGMT Theorems from the case where the underlying Gaussian matrix in the primary process has iid rows to where it has independent but non-identically-distributed ones. The new CGMT is applied to the problems of multi-source Gaussian regression, as well as to binary classification of general Gaussian mixture models.

Precise Asymptotic Analysis of Deep Random Feature Models

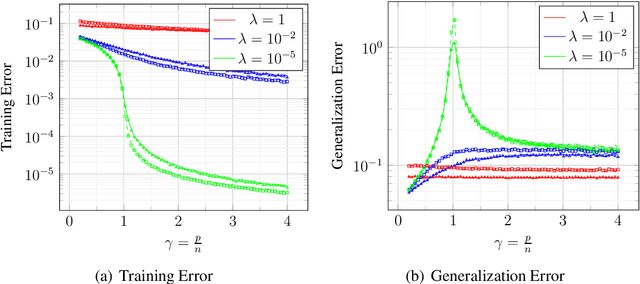
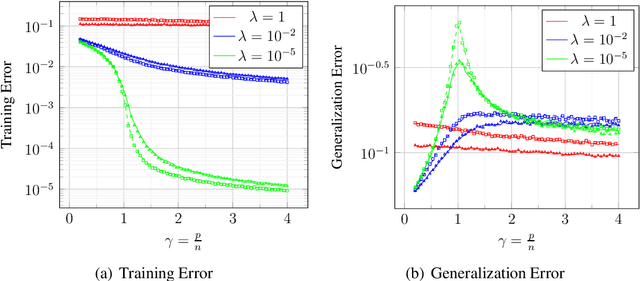
We provide exact asymptotic expressions for the performance of regression by an $L-$layer deep random feature (RF) model, where the input is mapped through multiple random embedding and non-linear activation functions. For this purpose, we establish two key steps: First, we prove a novel universality result for RF models and deterministic data, by which we demonstrate that a deep random feature model is equivalent to a deep linear Gaussian model that matches it in the first and second moments, at each layer. Second, we make use of the convex Gaussian Min-Max theorem multiple times to obtain the exact behavior of deep RF models. We further characterize the variation of the eigendistribution in different layers of the equivalent Gaussian model, demonstrating that depth has a tangible effect on model performance despite the fact that only the last layer of the model is being trained.

Double Descent in Random Feature Models: Precise Asymptotic Analysis for General Convex Regularization

We prove rigorous results on the double descent phenomenon in random features (RF) model by employing the powerful Convex Gaussian Min-Max Theorem (CGMT) in a novel multi-level manner. Using this technique, we provide precise asymptotic expressions for the generalization of RF regression under a broad class of convex regularization terms including arbitrary separable functions. We further compute our results for the combination of $\ell_1$ and $\ell_2$ regularization case, known as elastic net, and present numerical studies about it. We numerically demonstrate the predictive capacity of our framework, and show experimentally that the predicted test error is accurate even in the non-asymptotic regime.