Double Descent in Random Feature Models: Precise Asymptotic Analysis for General Convex Regularization

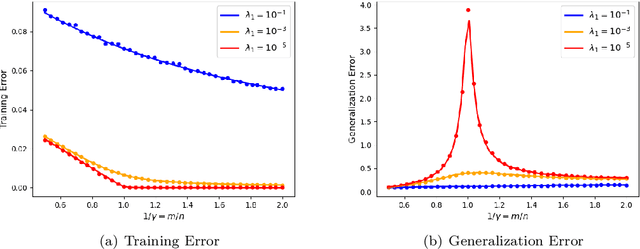
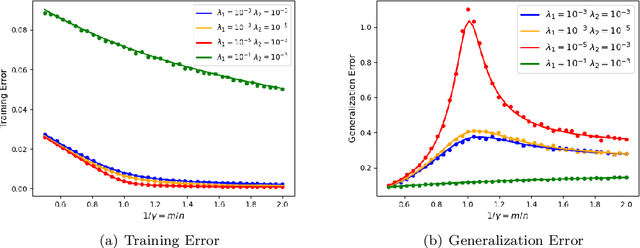
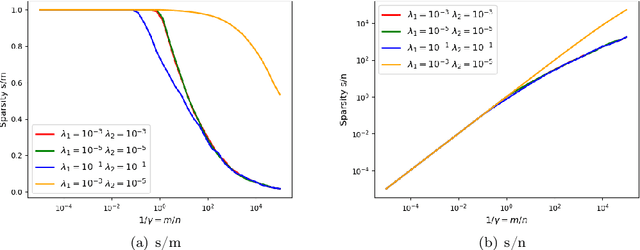
We prove rigorous results on the double descent phenomenon in random features (RF) model by employing the powerful Convex Gaussian Min-Max Theorem (CGMT) in a novel multi-level manner. Using this technique, we provide precise asymptotic expressions for the generalization of RF regression under a broad class of convex regularization terms including arbitrary separable functions. We further compute our results for the combination of $\ell_1$ and $\ell_2$ regularization case, known as elastic net, and present numerical studies about it. We numerically demonstrate the predictive capacity of our framework, and show experimentally that the predicted test error is accurate even in the non-asymptotic regime.