Universality in Transfer Learning for Linear Models

Transfer learning is an attractive framework for problems where there is a paucity of data, or where data collection is costly. One common approach to transfer learning is referred to as "model-based", and involves using a model that is pretrained on samples from a source distribution, which is easier to acquire, and then fine-tuning the model on a few samples from the target distribution. The hope is that, if the source and target distributions are ``close", then the fine-tuned model will perform well on the target distribution even though it has seen only a few samples from it. In this work, we study the problem of transfer learning in linear models for both regression and binary classification. In particular, we consider the use of stochastic gradient descent (SGD) on a linear model initialized with pretrained weights and using a small training data set from the target distribution. In the asymptotic regime of large models, we provide an exact and rigorous analysis and relate the generalization errors (in regression) and classification errors (in binary classification) for the pretrained and fine-tuned models. In particular, we give conditions under which the fine-tuned model outperforms the pretrained one. An important aspect of our work is that all the results are "universal", in the sense that they depend only on the first and second order statistics of the target distribution. They thus extend well beyond the standard Gaussian assumptions commonly made in the literature.

One-Bit Quantization and Sparsification for Multiclass Linear Classification via Regularized Regression

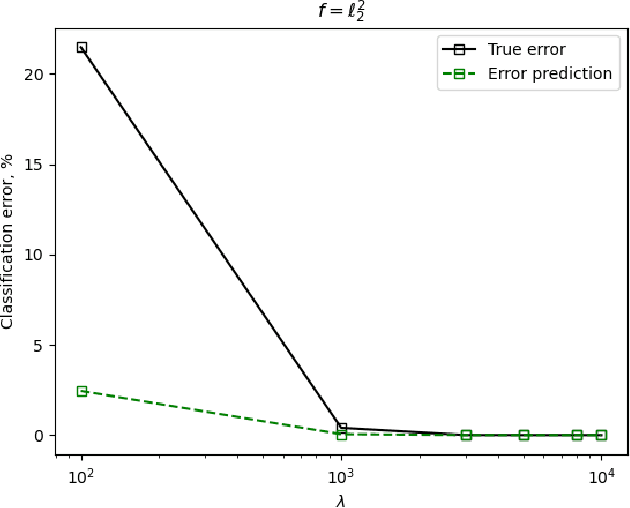
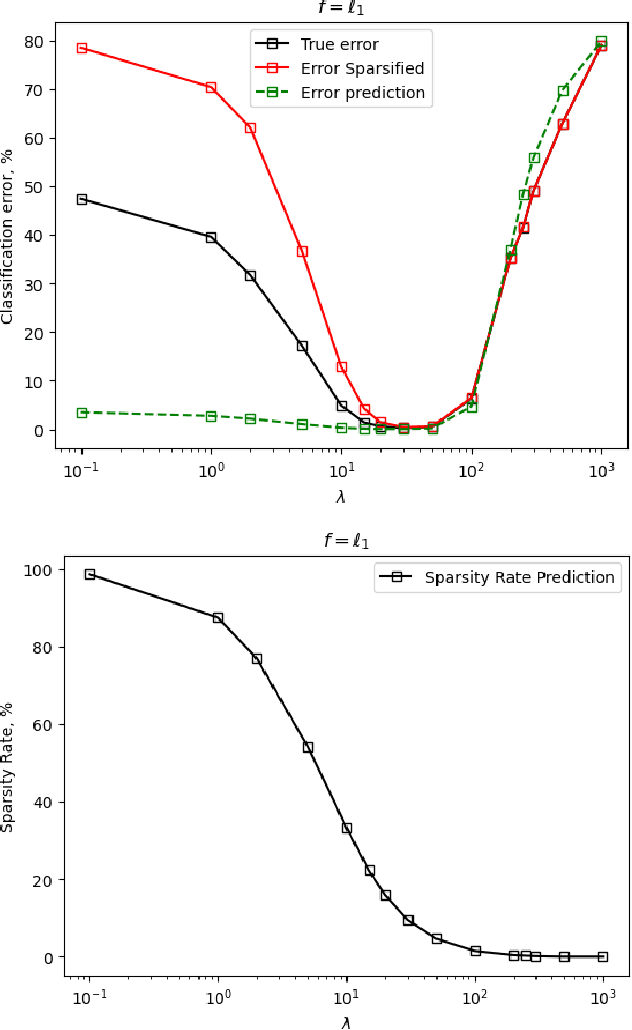
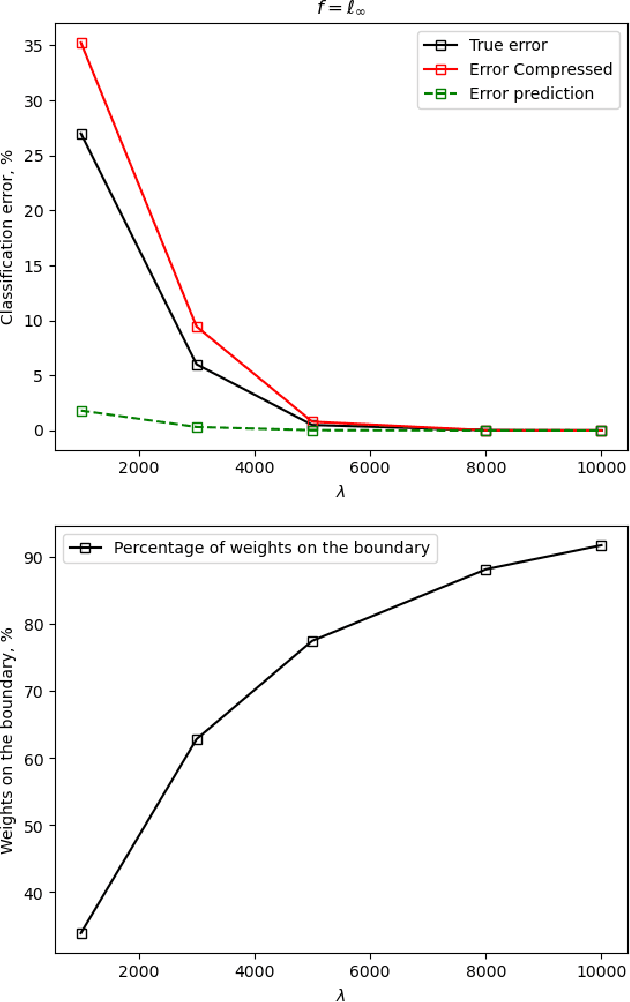
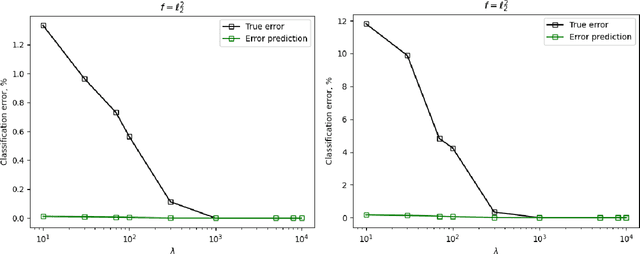
We study the use of linear regression for multiclass classification in the over-parametrized regime where some of the training data is mislabeled. In such scenarios it is necessary to add an explicit regularization term, $\lambda f(w)$, for some convex function $f(\cdot)$, to avoid overfitting the mislabeled data. In our analysis, we assume that the data is sampled from a Gaussian Mixture Model with equal class sizes, and that a proportion $c$ of the training labels is corrupted for each class. Under these assumptions, we prove that the best classification performance is achieved when $f(\cdot) = \|\cdot\|^2_2$ and $\lambda \to \infty$. We then proceed to analyze the classification errors for $f(\cdot) = \|\cdot\|_1$ and $f(\cdot) = \|\cdot\|_\infty$ in the large $\lambda$ regime and notice that it is often possible to find sparse and one-bit solutions, respectively, that perform almost as well as the one corresponding to $f(\cdot) = \|\cdot\|_2^2$.

A Novel Gaussian Min-Max Theorem and its Applications

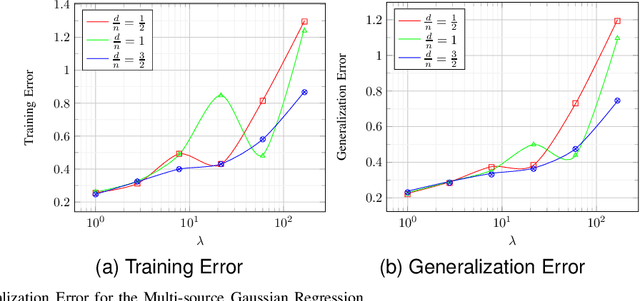
A celebrated result by Gordon allows one to compare the min-max behavior of two Gaussian processes if certain inequality conditions are met. The consequences of this result include the Gaussian min-max (GMT) and convex Gaussian min-max (CGMT) theorems which have had far-reaching implications in high-dimensional statistics, machine learning, non-smooth optimization, and signal processing. Both theorems rely on a pair of Gaussian processes, first identified by Slepian, that satisfy Gordon's comparison inequalities. To date, no other pair of Gaussian processes satisfying these inequalities has been discovered. In this paper, we identify such a new pair. The resulting theorems extend the classical GMT and CGMT Theorems from the case where the underlying Gaussian matrix in the primary process has iid rows to where it has independent but non-identically-distributed ones. The new CGMT is applied to the problems of multi-source Gaussian regression, as well as to binary classification of general Gaussian mixture models.

Regularized Linear Regression for Binary Classification

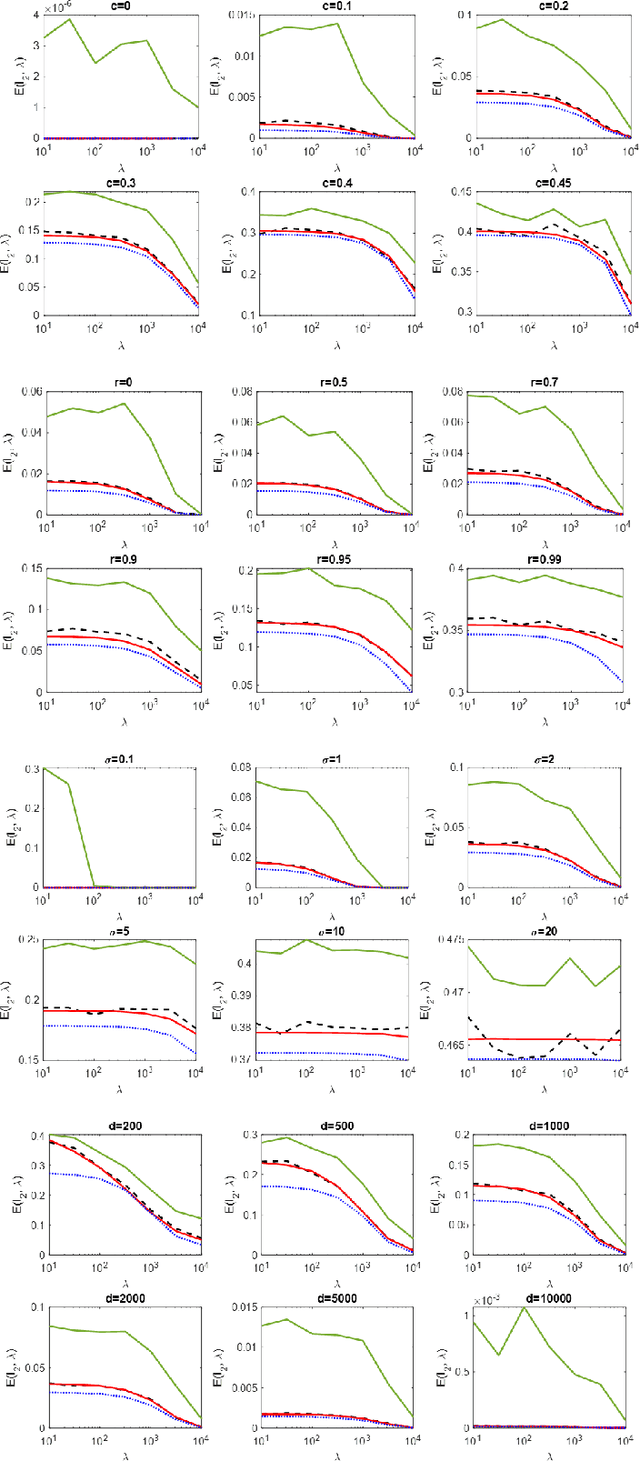
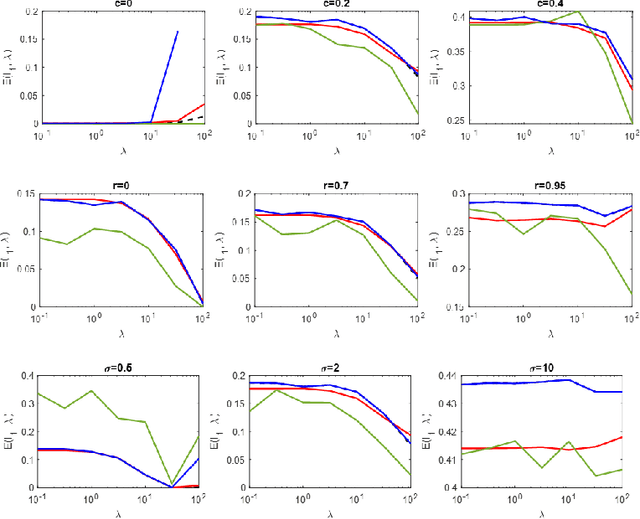
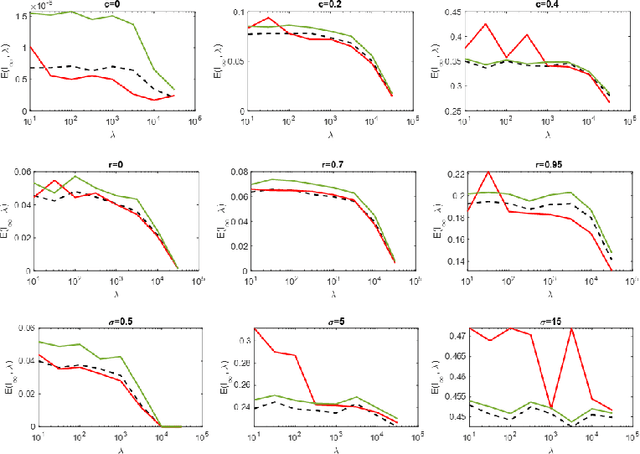
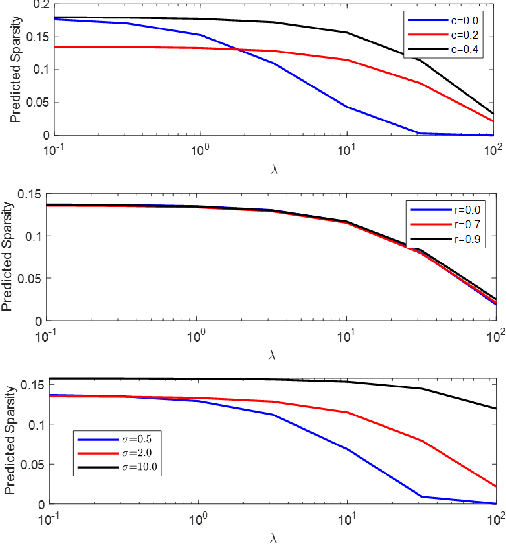
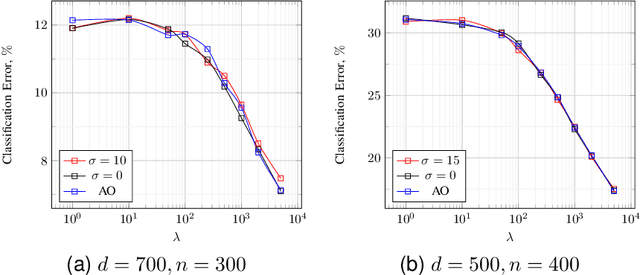
Regularized linear regression is a promising approach for binary classification problems in which the training set has noisy labels since the regularization term can help to avoid interpolating the mislabeled data points. In this paper we provide a systematic study of the effects of the regularization strength on the performance of linear classifiers that are trained to solve binary classification problems by minimizing a regularized least-squares objective. We consider the over-parametrized regime and assume that the classes are generated from a Gaussian Mixture Model (GMM) where a fraction $c<\frac{1}{2}$ of the training data is mislabeled. Under these assumptions, we rigorously analyze the classification errors resulting from the application of ridge, $\ell_1$, and $\ell_\infty$ regression. In particular, we demonstrate that ridge regression invariably improves the classification error. We prove that $\ell_1$ regularization induces sparsity and observe that in many cases one can sparsify the solution by up to two orders of magnitude without any considerable loss of performance, even though the GMM has no underlying sparsity structure. For $\ell_\infty$ regularization we show that, for large enough regularization strength, the optimal weights concentrate around two values of opposite sign. We observe that in many cases the corresponding "compression" of each weight to a single bit leads to very little loss in performance. These latter observations can have significant practical ramifications.

The Generalization Error of Stochastic Mirror Descent on Over-Parametrized Linear Models

Despite being highly over-parametrized, and having the ability to fully interpolate the training data, deep networks are known to generalize well to unseen data. It is now understood that part of the reason for this is that the training algorithms used have certain implicit regularization properties that ensure interpolating solutions with "good" properties are found. This is best understood in linear over-parametrized models where it has been shown that the celebrated stochastic gradient descent (SGD) algorithm finds an interpolating solution that is closest in Euclidean distance to the initial weight vector. Different regularizers, replacing Euclidean distance with Bregman divergence, can be obtained if we replace SGD with stochastic mirror descent (SMD). Empirical observations have shown that in the deep network setting, SMD achieves a generalization performance that is different from that of SGD (and which depends on the choice of SMD's potential function. In an attempt to begin to understand this behavior, we obtain the generalization error of SMD for over-parametrized linear models for a binary classification problem where the two classes are drawn from a Gaussian mixture model. We present simulation results that validate the theory and, in particular, introduce two data models, one for which SMD with an $\ell_2$ regularizer (i.e., SGD) outperforms SMD with an $\ell_1$ regularizer, and one for which the reverse happens.