Regularized Linear Regression for Binary Classification
Paper and Code
Nov 03, 2023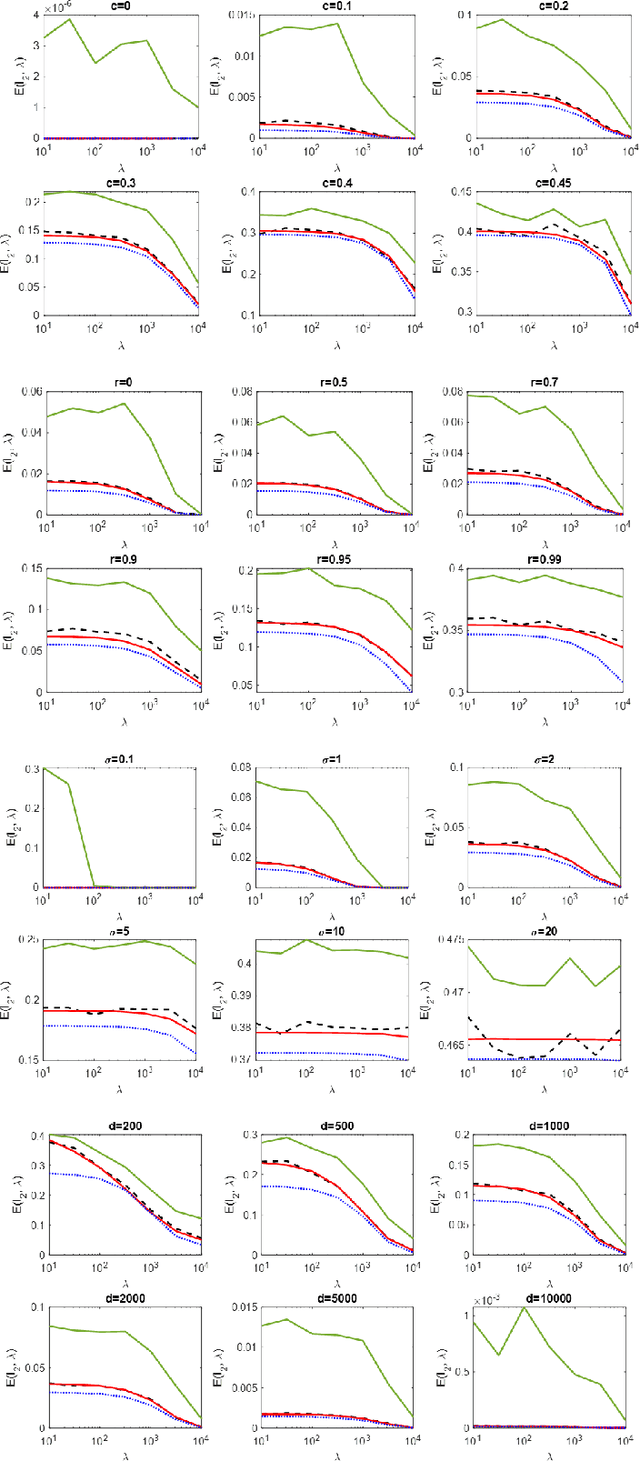
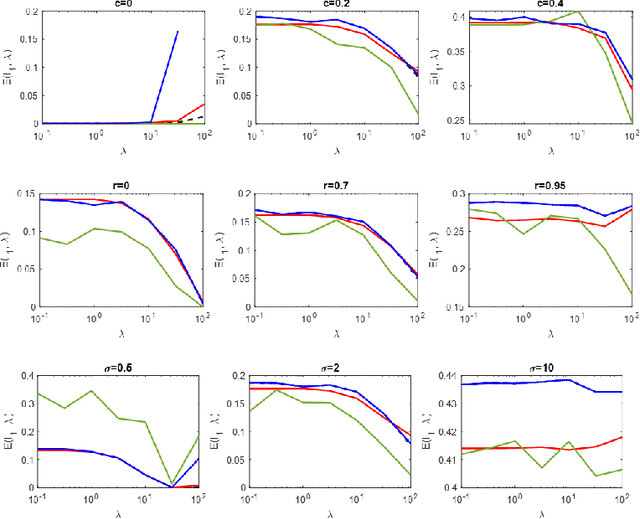
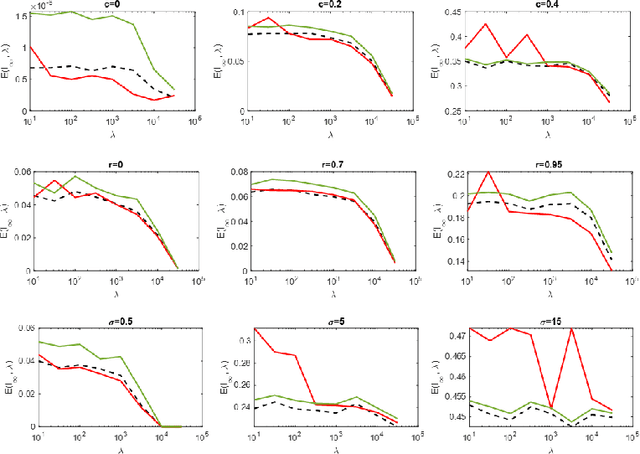
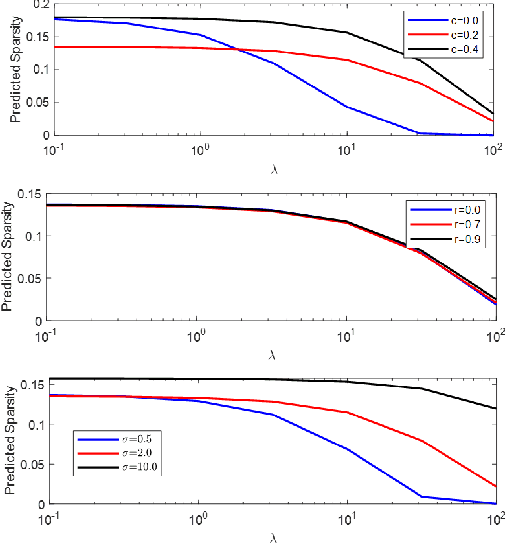
Regularized linear regression is a promising approach for binary classification problems in which the training set has noisy labels since the regularization term can help to avoid interpolating the mislabeled data points. In this paper we provide a systematic study of the effects of the regularization strength on the performance of linear classifiers that are trained to solve binary classification problems by minimizing a regularized least-squares objective. We consider the over-parametrized regime and assume that the classes are generated from a Gaussian Mixture Model (GMM) where a fraction $c<\frac{1}{2}$ of the training data is mislabeled. Under these assumptions, we rigorously analyze the classification errors resulting from the application of ridge, $\ell_1$, and $\ell_\infty$ regression. In particular, we demonstrate that ridge regression invariably improves the classification error. We prove that $\ell_1$ regularization induces sparsity and observe that in many cases one can sparsify the solution by up to two orders of magnitude without any considerable loss of performance, even though the GMM has no underlying sparsity structure. For $\ell_\infty$ regularization we show that, for large enough regularization strength, the optimal weights concentrate around two values of opposite sign. We observe that in many cases the corresponding "compression" of each weight to a single bit leads to very little loss in performance. These latter observations can have significant practical ramifications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge