Achieving the fundamental convergence-communication tradeoff with Differentially Quantized Gradient Descent
Paper and Code
Feb 06, 2020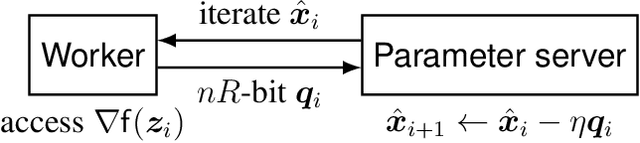

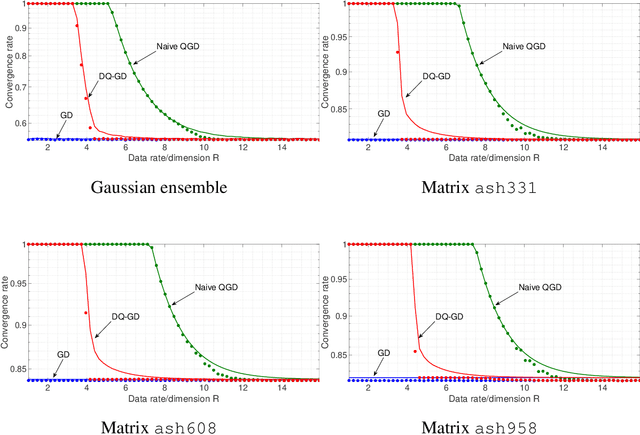
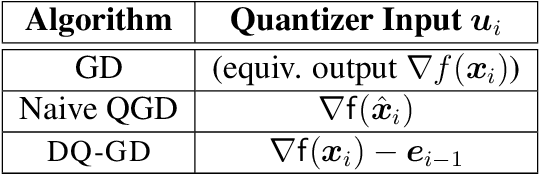
The problem of reducing the communication cost in distributed training through gradient quantization is considered. For the class of smooth and strongly convex objective functions, we characterize the minimum achievable linear convergence rate for a given number of bits per problem dimension $n$. We propose Differentially Quantized Gradient Descent, a quantization algorithm with error compensation, and prove that it achieves the fundamental tradeoff between communication rate and convergence rate as $n$ goes to infinity. In contrast, the naive quantizer that compresses the current gradient directly fails to achieve that optimal tradeoff. Experimental results on both simulated and real-world least-squares problems confirm our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge