Xiangrong Zeng
China Agricultural University
Amplify Adjacent Token Differences: Enhancing Long Chain-of-Thought Reasoning with Shift-FFN
May 22, 2025Abstract:Recently, models such as OpenAI-o1 and DeepSeek-R1 have demonstrated remarkable performance on complex reasoning tasks through Long Chain-of-Thought (Long-CoT) reasoning. Although distilling this capability into student models significantly enhances their performance, this paper finds that fine-tuning LLMs with full parameters or LoRA with a low rank on long CoT data often leads to Cyclical Reasoning, where models repeatedly reiterate previous inference steps until the maximum length limit. Further analysis reveals that smaller differences in representations between adjacent tokens correlates with a higher tendency toward Cyclical Reasoning. To mitigate this issue, this paper proposes Shift Feedforward Networks (Shift-FFN), a novel approach that edits the current token's representation with the previous one before inputting it to FFN. This architecture dynamically amplifies the representation differences between adjacent tokens. Extensive experiments on multiple mathematical reasoning tasks demonstrate that LoRA combined with Shift-FFN achieves higher accuracy and a lower rate of Cyclical Reasoning across various data sizes compared to full fine-tuning and standard LoRA. Our data and code are available at https://anonymous.4open.science/r/Shift-FFN
TomatoScanner: phenotyping tomato fruit based on only RGB image
Mar 07, 2025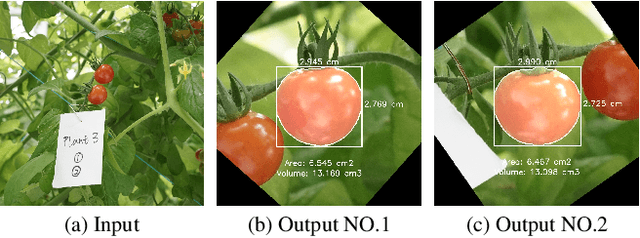
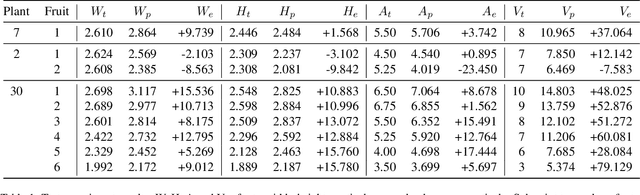
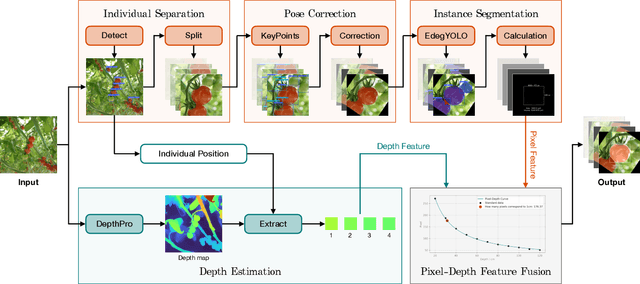
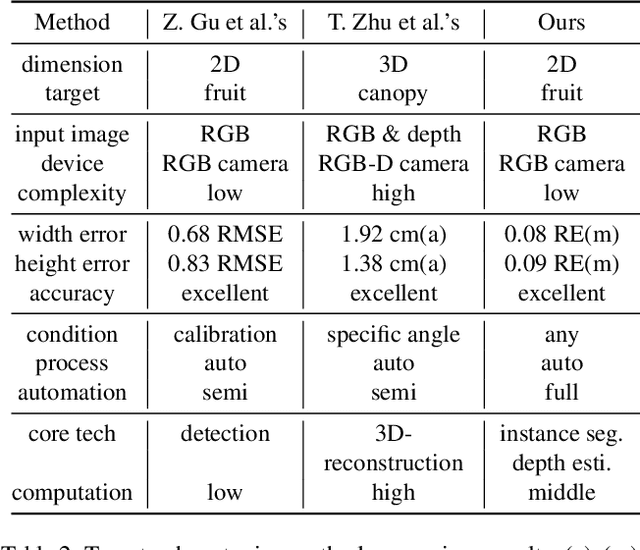
Abstract:In tomato greenhouse, phenotypic measurement is meaningful for researchers and farmers to monitor crop growth, thereby precisely control environmental conditions in time, leading to better quality and higher yield. Traditional phenotyping mainly relies on manual measurement, which is accurate but inefficient, more importantly, endangering the health and safety of people. Several studies have explored computer vision-based methods to replace manual phenotyping. However, the 2D-based need extra calibration, or cause destruction to fruit, or can only measure limited and meaningless traits. The 3D-based need extra depth camera, which is expensive and unacceptable for most farmers. In this paper, we propose a non-contact tomato fruit phenotyping method, titled TomatoScanner, where RGB image is all you need for input. First, pixel feature is extracted by instance segmentation of our proposed EdgeYOLO with preprocessing of individual separation and pose correction. Second, depth feature is extracted by depth estimation of Depth Pro. Third, pixel and depth feature are fused to output phenotype results in reality. We establish self-built Tomato Phenotype Dataset to test TomatoScanner, which achieves excellent phenotyping on width, height, vertical area and volume, with median relative error of 5.63%, 7.03%, -0.64% and 37.06%, respectively. We propose and add three innovative modules - EdgeAttention, EdgeLoss and EdgeBoost - into EdgeYOLO, to enhance the segmentation accuracy on edge portion. Precision and mean Edge Error greatly improve from 0.943 and 5.641% to 0.986 and 2.963%, respectively. Meanwhile, EdgeYOLO keeps lightweight and efficient, with 48.7 M weights size and 76.34 FPS. Codes and datasets: https://github.com/AlexTraveling/TomatoScanner.
Baichuan-M1: Pushing the Medical Capability of Large Language Models
Feb 18, 2025Abstract:The current generation of large language models (LLMs) is typically designed for broad, general-purpose applications, while domain-specific LLMs, especially in vertical fields like medicine, remain relatively scarce. In particular, the development of highly efficient and practical LLMs for the medical domain is challenging due to the complexity of medical knowledge and the limited availability of high-quality data. To bridge this gap, we introduce Baichuan-M1, a series of large language models specifically optimized for medical applications. Unlike traditional approaches that simply continue pretraining on existing models or apply post-training to a general base model, Baichuan-M1 is trained from scratch with a dedicated focus on enhancing medical capabilities. Our model is trained on 20 trillion tokens and incorporates a range of effective training methods that strike a balance between general capabilities and medical expertise. As a result, Baichuan-M1 not only performs strongly across general domains such as mathematics and coding but also excels in specialized medical fields. We have open-sourced Baichuan-M1-14B, a mini version of our model, which can be accessed through the following links.
Baichuan 2: Open Large-scale Language Models
Sep 20, 2023Abstract:Large language models (LLMs) have demonstrated remarkable performance on a variety of natural language tasks based on just a few examples of natural language instructions, reducing the need for extensive feature engineering. However, most powerful LLMs are closed-source or limited in their capability for languages other than English. In this technical report, we present Baichuan 2, a series of large-scale multilingual language models containing 7 billion and 13 billion parameters, trained from scratch, on 2.6 trillion tokens. Baichuan 2 matches or outperforms other open-source models of similar size on public benchmarks like MMLU, CMMLU, GSM8K, and HumanEval. Furthermore, Baichuan 2 excels in vertical domains such as medicine and law. We will release all pre-training model checkpoints to benefit the research community in better understanding the training dynamics of Baichuan 2.
Path-based knowledge reasoning with textual semantic information for medical knowledge graph completion
May 28, 2021

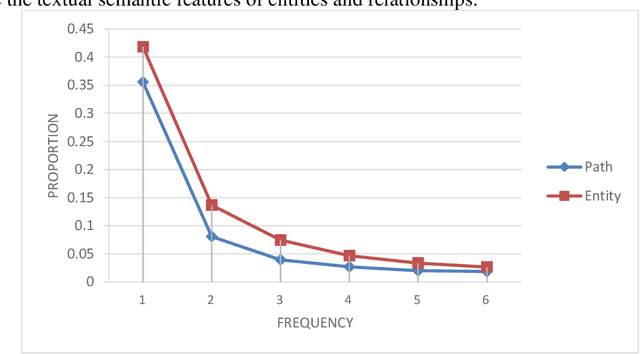

Abstract:Background Knowledge graphs (KGs), especially medical knowledge graphs, are often significantly incomplete, so it necessitating a demand for medical knowledge graph completion (MedKGC). MedKGC can find new facts based on the exited knowledge in the KGs. The path-based knowledge reasoning algorithm is one of the most important approaches to this task. This type of method has received great attention in recent years because of its high performance and interpretability. In fact, traditional methods such as path ranking algorithm (PRA) take the paths between an entity pair as atomic features. However, the medical KGs are very sparse, which makes it difficult to model effective semantic representation for extremely sparse path features. The sparsity in the medical KGs is mainly reflected in the long-tailed distribution of entities and paths. Previous methods merely consider the context structure in the paths of the knowledge graph and ignore the textual semantics of the symbols in the path. Therefore, their performance cannot be further improved due to the two aspects of entity sparseness and path sparseness. To address the above issues, this paper proposes two novel path-based reasoning methods to solve the sparsity issues of entity and path respectively, which adopts the textual semantic information of entities and paths for MedKGC. By using the pre-trained model BERT, combining the textual semantic representations of the entities and the relationships, we model the task of symbolic reasoning in the medical KG as a numerical computing issue in textual semantic representation.
Joint Entity and Relation Extraction with Set Prediction Networks
Nov 05, 2020



Abstract:The joint entity and relation extraction task aims to extract all relational triples from a sentence. In essence, the relational triples contained in a sentence are unordered. However, previous seq2seq based models require to convert the set of triples into a sequence in the training phase. To break this bottleneck, we treat joint entity and relation extraction as a direct set prediction problem, so that the extraction model can get rid of the burden of predicting the order of multiple triples. To solve this set prediction problem, we propose networks featured by transformers with non-autoregressive parallel decoding. Unlike autoregressive approaches that generate triples one by one in a certain order, the proposed networks directly output the final set of triples in one shot. Furthermore, we also design a set-based loss that forces unique predictions via bipartite matching. Compared with cross-entropy loss that highly penalizes small shifts in triple order, the proposed bipartite matching loss is invariant to any permutation of predictions; thus, it can provide the proposed networks with a more accurate training signal by ignoring triple order and focusing on relation types and entities. Experiments on two benchmark datasets show that our proposed model significantly outperforms current state-of-the-art methods. Training code and trained models will be available at http://github.com/DianboWork/SPN4RE.
The Ordered Weighted $\ell_1$ Norm: Atomic Formulation, Projections, and Algorithms
Apr 10, 2015


Abstract:The ordered weighted $\ell_1$ norm (OWL) was recently proposed, with two different motivations: its good statistical properties as a sparsity promoting regularizer; the fact that it generalizes the so-called {\it octagonal shrinkage and clustering algorithm for regression} (OSCAR), which has the ability to cluster/group regression variables that are highly correlated. This paper contains several contributions to the study and application of OWL regularization: the derivation of the atomic formulation of the OWL norm; the derivation of the dual of the OWL norm, based on its atomic formulation; a new and simpler derivation of the proximity operator of the OWL norm; an efficient scheme to compute the Euclidean projection onto an OWL ball; the instantiation of the conditional gradient (CG, also known as Frank-Wolfe) algorithm for linear regression problems under OWL regularization; the instantiation of accelerated projected gradient algorithms for the same class of problems. Finally, a set of experiments give evidence that accelerated projected gradient algorithms are considerably faster than CG, for the class of problems considered.
Decreasing Weighted Sorted $\ell_1$ Regularization
Apr 11, 2014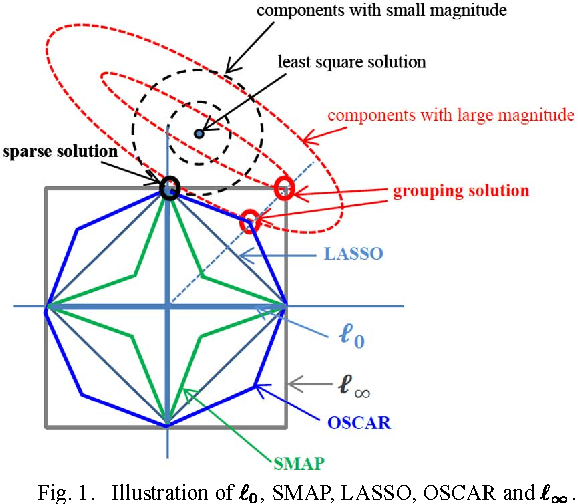
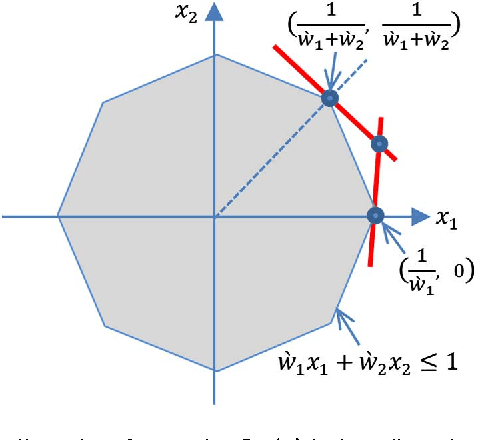
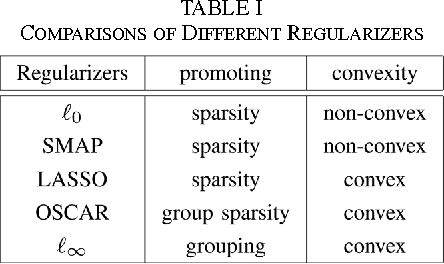
Abstract:We consider a new family of regularizers, termed {\it weighted sorted $\ell_1$ norms} (WSL1), which generalizes the recently introduced {\it octagonal shrinkage and clustering algorithm for regression} (OSCAR) and also contains the $\ell_1$ and $\ell_{\infty}$ norms as particular instances. We focus on a special case of the WSL1, the {\sl decreasing WSL1} (DWSL1), where the elements of the argument vector are sorted in non-increasing order and the weights are also non-increasing. In this paper, after showing that the DWSL1 is indeed a norm, we derive two key tools for its use as a regularizer: the dual norm and the Moreau proximity operator.
Robust Binary Fused Compressive Sensing using Adaptive Outlier Pursuit
Mar 20, 2014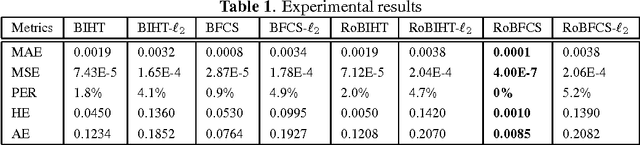
Abstract:We propose a new method, {\it robust binary fused compressive sensing} (RoBFCS), to recover sparse piece-wise smooth signals from 1-bit compressive measurements. The proposed method is a modification of our previous {\it binary fused compressive sensing} (BFCS) algorithm, which is based on the {\it binary iterative hard thresholding} (BIHT) algorithm. As in BIHT, the data term of the objective function is a one-sided $\ell_1$ (or $\ell_2$) norm. Experiments show that the proposed algorithm is able to take advantage of the piece-wise smoothness of the original signal and detect sign flips and correct them, achieving more accurate recovery than BFCS and BIHT.
Exploiting Two-Dimensional Group Sparsity in 1-Bit Compressive Sensing
Feb 21, 2014Abstract:We propose a new approach, {\it two-dimensional fused binary compressive sensing} (2DFBCS) to recover 2D sparse piece-wise signals from 1-bit measurements, exploiting 2D group sparsity for 1-bit compressive sensing recovery. The proposed method is a modified 2D version of the previous {\it binary iterative hard thresholding} (2DBIHT) algorithm, where the objective function includes a 2D one-sided $\ell_1$ (or $\ell_2$) penalty function encouraging agreement with the observed data, an indicator function of $K$-sparsity, and a total variation (TV) or modified TV (MTV) constraint. The subgradient of the 2D one-sided $\ell_1$ (or $\ell_2$) penalty and the projection onto the $K$-sparsity and TV or MTV constraint can be computed efficiently, allowing the appliaction of algorithms of the {\it forward-backward splitting} (a.k.a. {\it iterative shrinkage-thresholding}) family. Experiments on the recovery of 2D sparse piece-wise smooth signals show that the proposed approach is able to take advantage of the piece-wise smoothness of the original signal, achieving more accurate recovery than 2DBIHT. More specifically, 2DFBCS with the MTV and the $\ell_2$ penalty performs best amongst the algorithms tested.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge