Decreasing Weighted Sorted $\ell_1$ Regularization
Paper and Code
Apr 11, 2014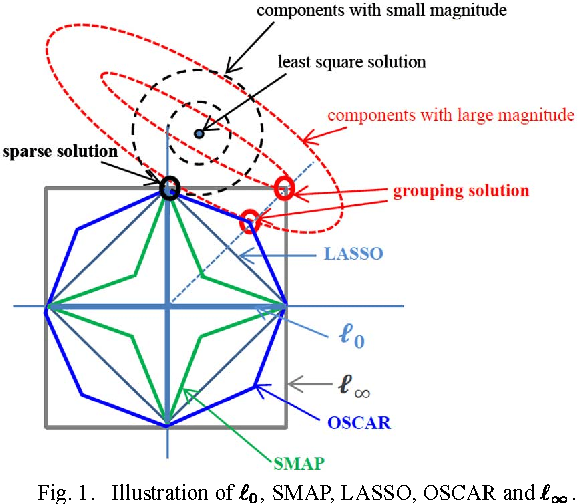
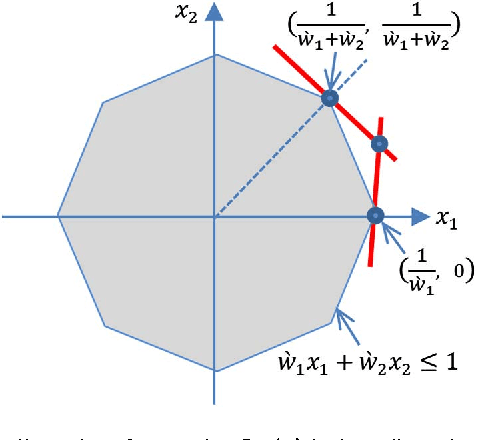
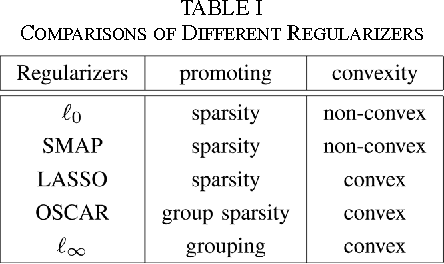
We consider a new family of regularizers, termed {\it weighted sorted $\ell_1$ norms} (WSL1), which generalizes the recently introduced {\it octagonal shrinkage and clustering algorithm for regression} (OSCAR) and also contains the $\ell_1$ and $\ell_{\infty}$ norms as particular instances. We focus on a special case of the WSL1, the {\sl decreasing WSL1} (DWSL1), where the elements of the argument vector are sorted in non-increasing order and the weights are also non-increasing. In this paper, after showing that the DWSL1 is indeed a norm, we derive two key tools for its use as a regularizer: the dual norm and the Moreau proximity operator.
* 5 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge