Multi-Frequency Joint Community Detection and Phase Synchronization

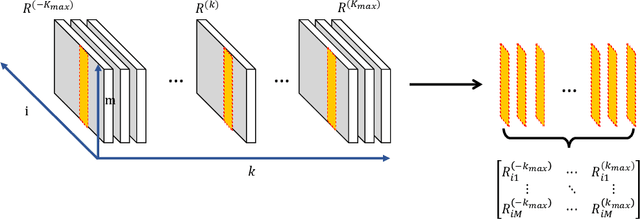
This paper studies the joint community detection and phase synchronization problem on the \textit{stochastic block model with relative phase}, where each node is associated with a phase. This problem, with a variety of real-world applications, aims to recover community memberships and associated phases simultaneously. By studying the maximum likelihood estimation formulation, we show that this problem exhibits a \textit{``multi-frequency''} structure. To this end, two simple yet efficient algorithms that leverage information across multiple frequencies are proposed. The former is a spectral method based on the novel multi-frequency column-pivoted QR factorization, and the latter is an iterative multi-frequency generalized power method. Numerical experiments indicate our proposed algorithms outperform state-of-the-art algorithms, in recovering community memberships and associated phases.