Evidential Deep Learning for Uncertainty Quantification and Out-of-Distribution Detection in Jet Identification using Deep Neural Networks

Current methods commonly used for uncertainty quantification (UQ) in deep learning (DL) models utilize Bayesian methods which are computationally expensive and time-consuming. In this paper, we provide a detailed study of UQ based on evidential deep learning (EDL) for deep neural network models designed to identify jets in high energy proton-proton collisions at the Large Hadron Collider and explore its utility in anomaly detection. EDL is a DL approach that treats learning as an evidence acquisition process designed to provide confidence (or epistemic uncertainty) about test data. Using publicly available datasets for jet classification benchmarking, we explore hyperparameter optimizations for EDL applied to the challenge of UQ for jet identification. We also investigate how the uncertainty is distributed for each jet class, how this method can be implemented for the detection of anomalies, how the uncertainty compares with Bayesian ensemble methods, and how the uncertainty maps onto latent spaces for the models. Our studies uncover some pitfalls of EDL applied to anomaly detection and a more effective way to quantify uncertainty from EDL as compared with the foundational EDL setup. These studies illustrate a methodological approach to interpreting EDL in jet classification models, providing new insights on how EDL quantifies uncertainty and detects out-of-distribution data which may lead to improved EDL methods for DL models applied to classification tasks.

FAIR AI Models in High Energy Physics

The findable, accessible, interoperable, and reusable (FAIR) data principles have provided a framework for examining, evaluating, and improving how we share data with the aim of facilitating scientific discovery. Efforts have been made to generalize these principles to research software and other digital products. Artificial intelligence (AI) models -- algorithms that have been trained on data rather than explicitly programmed -- are an important target for this because of the ever-increasing pace with which AI is transforming scientific and engineering domains. In this paper, we propose a practical definition of FAIR principles for AI models and create a FAIR AI project template that promotes adherence to these principles. We demonstrate how to implement these principles using a concrete example from experimental high energy physics: a graph neural network for identifying Higgs bosons decaying to bottom quarks. We study the robustness of these FAIR AI models and their portability across hardware architectures and software frameworks, and report new insights on the interpretability of AI predictions by studying the interplay between FAIR datasets and AI models. Enabled by publishing FAIR AI models, these studies pave the way toward reliable and automated AI-driven scientific discovery.

Interpretability of an Interaction Network for identifying $H \rightarrow b\bar{b}$ jets

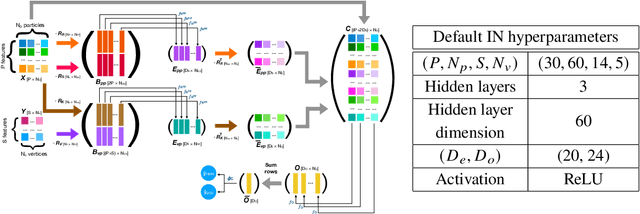
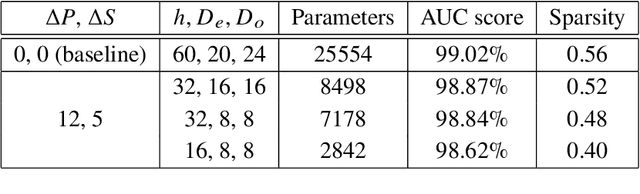
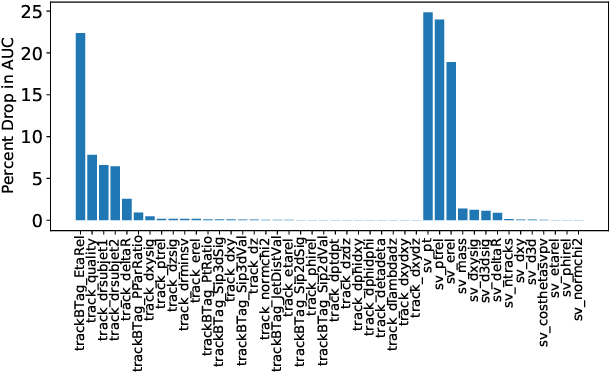
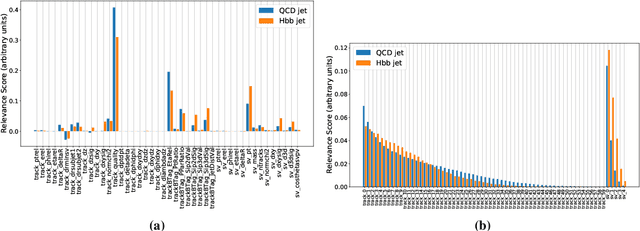
Multivariate techniques and machine learning models have found numerous applications in High Energy Physics (HEP) research over many years. In recent times, AI models based on deep neural networks are becoming increasingly popular for many of these applications. However, neural networks are regarded as black boxes -- because of their high degree of complexity it is often quite difficult to quantitatively explain the output of a neural network by establishing a tractable input-output relationship and information propagation through the deep network layers. As explainable AI (xAI) methods are becoming more popular in recent years, we explore interpretability of AI models by examining an Interaction Network (IN) model designed to identify boosted $H\to b\bar{b}$ jets amid QCD background. We explore different quantitative methods to demonstrate how the classifier network makes its decision based on the inputs and how this information can be harnessed to reoptimize the model-making it simpler yet equally effective. We additionally illustrate the activity of hidden layers within the IN model as Neural Activation Pattern (NAP) diagrams. Our experiments suggest NAP diagrams reveal important information about how information is conveyed across the hidden layers of deep model. These insights can be useful to effective model reoptimization and hyperparameter tuning.

A Detailed Study of Interpretability of Deep Neural Network based Top Taggers

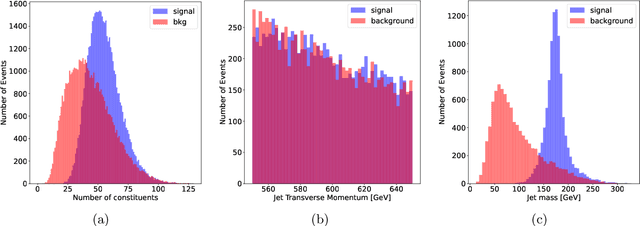
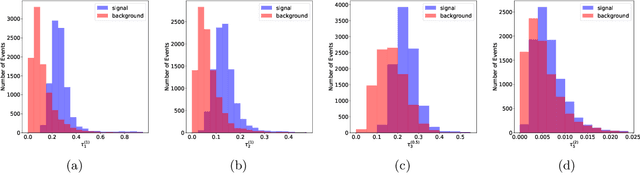
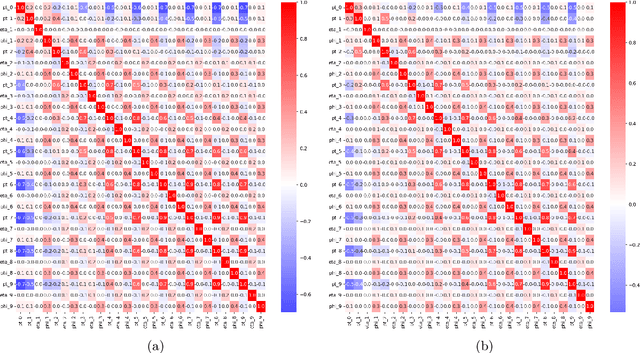
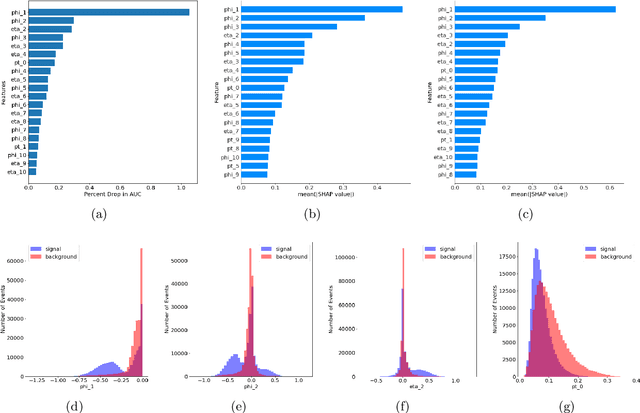
Recent developments in the methods of explainable AI (xAI) methods allow us to explore the inner workings of deep neural networks (DNNs), revealing crucial information about input-output relationships and realizing how data connects with machine learning models. In this paper we explore interpretability of DNN models designed for identifying jets coming from top quark decay in the high energy proton-proton collisions at the Large Hadron Collider (LHC). We review a subset of existing such top tagger models and explore different quantitative methods to identify which features play the most important roles in identifying the top jets. We also investigate how and why feature importance varies across different xAI metrics, how feature correlations impact their explainability, and how latent space representations encode information as well as correlate with physically meaningful quantities. Our studies uncover some major pitfalls of existing xAI methods and illustrate how they can be overcome to obtain consistent and meaningful interpretation of these models. We additionally illustrate the activity of hidden layers as Neural Activation Pattern (NAP) diagrams and demonstrate how they can be used to understand how DNNs relay information across the layers and how this understanding can help us to make such models significantly simpler by allowing effective model reoptimization and hyperparameter tuning. While the primary focus of this work remains a detailed study of interpretability of DNN-based top tagger models, it also features state-of-the art performance obtained from modified implementation of existing networks.

Data Science and Machine Learning in Education

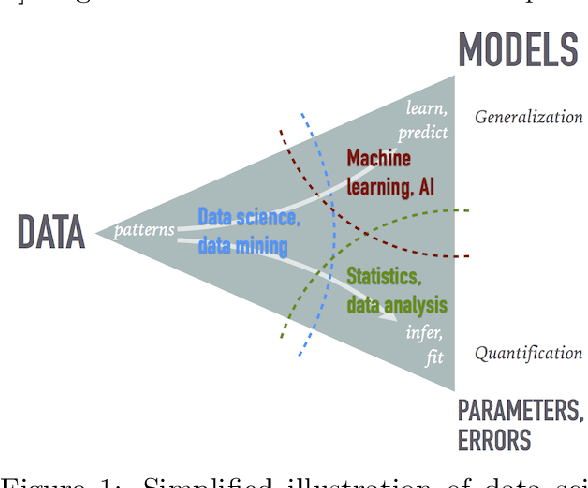
The growing role of data science (DS) and machine learning (ML) in high-energy physics (HEP) is well established and pertinent given the complex detectors, large data, sets and sophisticated analyses at the heart of HEP research. Moreover, exploiting symmetries inherent in physics data have inspired physics-informed ML as a vibrant sub-field of computer science research. HEP researchers benefit greatly from materials widely available materials for use in education, training and workforce development. They are also contributing to these materials and providing software to DS/ML-related fields. Increasingly, physics departments are offering courses at the intersection of DS, ML and physics, often using curricula developed by HEP researchers and involving open software and data used in HEP. In this white paper, we explore synergies between HEP research and DS/ML education, discuss opportunities and challenges at this intersection, and propose community activities that will be mutually beneficial.

Explainable AI for High Energy Physics

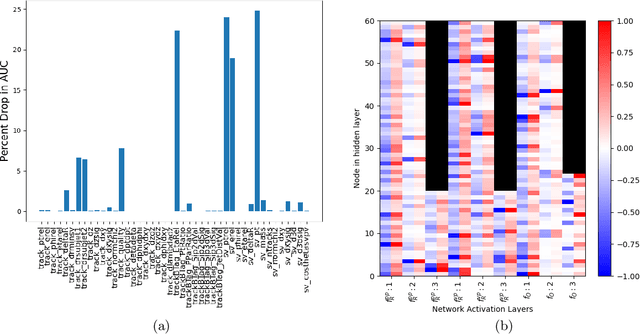
Neural Networks are ubiquitous in high energy physics research. However, these highly nonlinear parameterized functions are treated as \textit{black boxes}- whose inner workings to convey information and build the desired input-output relationship are often intractable. Explainable AI (xAI) methods can be useful in determining a neural model's relationship with data toward making it \textit{interpretable} by establishing a quantitative and tractable relationship between the input and the model's output. In this letter of interest, we explore the potential of using xAI methods in the context of problems in high energy physics.

Robust Learning of Physics Informed Neural Networks

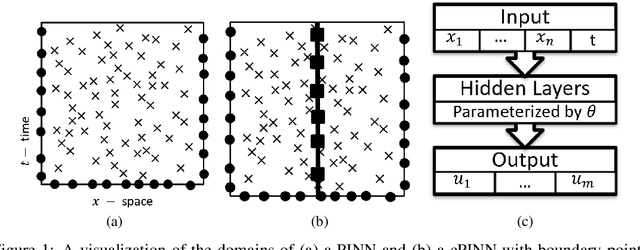
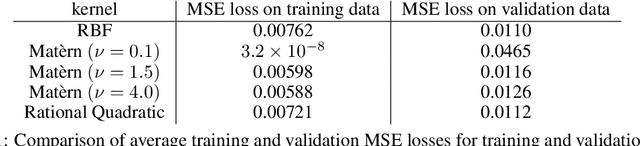
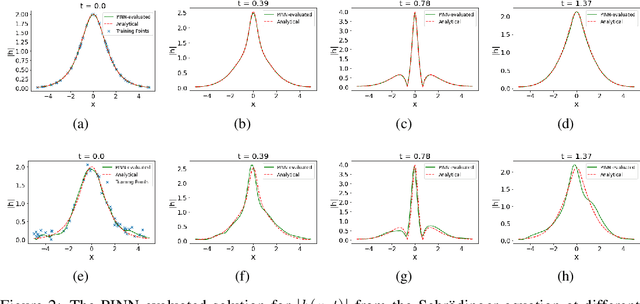
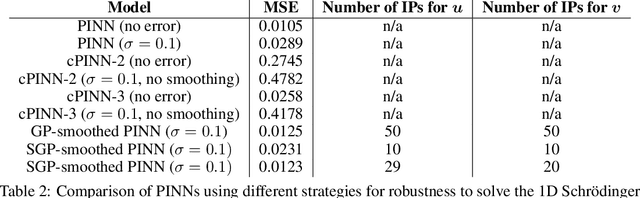
Physics-informed Neural Networks (PINNs) have been shown to be effective in solving partial differential equations by capturing the physics induced constraints as a part of the training loss function. This paper shows that a PINN can be sensitive to errors in training data and overfit itself in dynamically propagating these errors over the domain of the solution of the PDE. It also shows how physical regularizations based on continuity criteria and conservation laws fail to address this issue and rather introduce problems of their own causing the deep network to converge to a physics-obeying local minimum instead of the global minimum. We introduce Gaussian Process (GP) based smoothing that recovers the performance of a PINN and promises a robust architecture against noise/errors in measurements. Additionally, we illustrate an inexpensive method of quantifying the evolution of uncertainty based on the variance estimation of GPs on boundary data. Robust PINN performance is also shown to be achievable by choice of sparse sets of inducing points based on sparsely induced GPs. We demonstrate the performance of our proposed methods and compare the results from existing benchmark models in literature for time-dependent Schr\"odinger and Burgers' equations.

Invariance-based Multi-Clustering of Latent Space Embeddings for Equivariant Learning

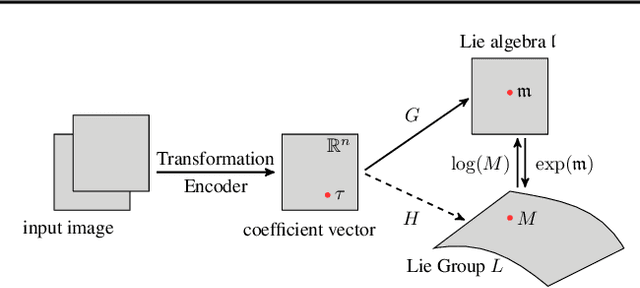
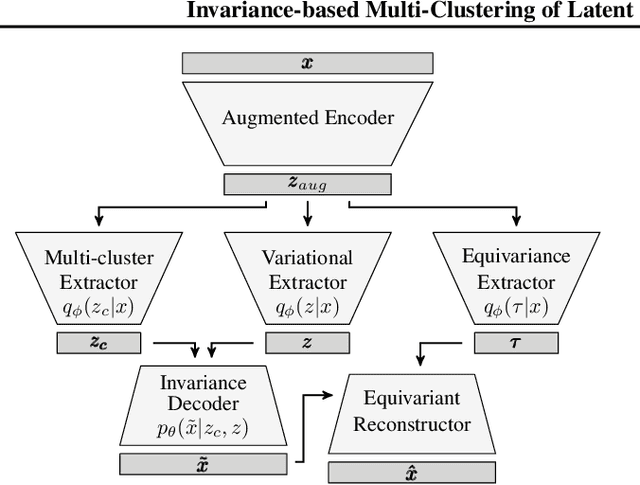
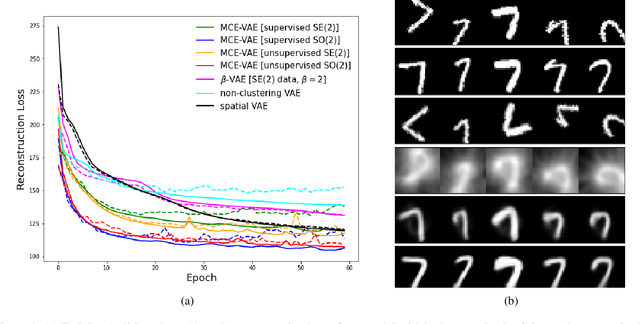
Variational Autoencoders (VAEs) have been shown to be remarkably effective in recovering model latent spaces for several computer vision tasks. However, currently trained VAEs, for a number of reasons, seem to fall short in learning invariant and equivariant clusters in latent space. Our work focuses on providing solutions to this problem and presents an approach to disentangle equivariance feature maps in a Lie group manifold by enforcing deep, group-invariant learning. Simultaneously implementing a novel separation of semantic and equivariant variables of the latent space representation, we formulate a modified Evidence Lower BOund (ELBO) by using a mixture model pdf like Gaussian mixtures for invariant cluster embeddings that allows superior unsupervised variational clustering. Our experiments show that this model effectively learns to disentangle the invariant and equivariant representations with significant improvements in the learning rate and an observably superior image recognition and canonical state reconstruction compared to the currently best deep learning models.