A Spectral Method for Joint Community Detection and Orthogonal Group Synchronization

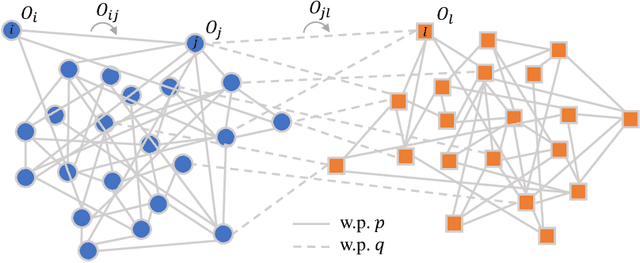
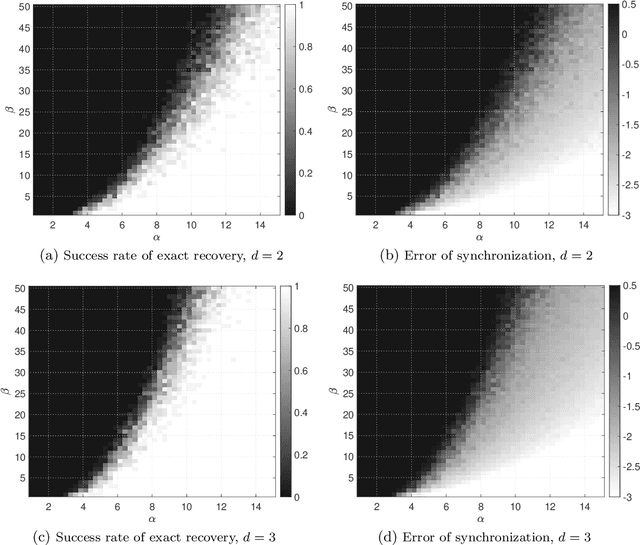
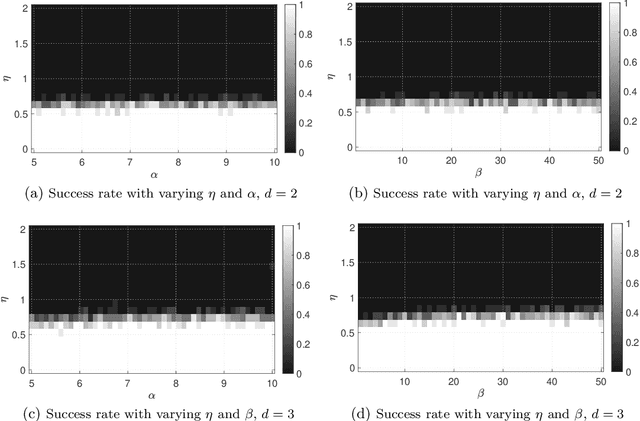
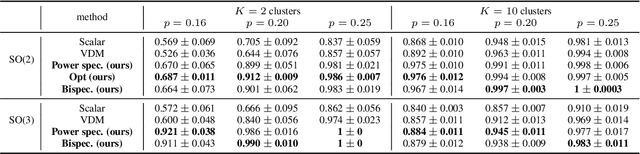
Community detection and orthogonal group synchronization are both fundamental problems with a variety of important applications in science and engineering. In this work, we consider the joint problem of community detection and orthogonal group synchronization which aims to recover the communities and perform synchronization simultaneously. To this end, we propose a simple algorithm that consists of a spectral decomposition step followed by a blockwise column pivoted QR factorization (CPQR). The proposed algorithm is efficient and scales linearly with the number of data points. We also leverage the recently developed `leave-one-out' technique to establish a near-optimal guarantee for exact recovery of the cluster memberships and stable recovery of the orthogonal transforms. Numerical experiments demonstrate the efficiency and efficacy of our algorithm and confirm our theoretical characterization of it.

End-to-end Alexa Device Arbitration

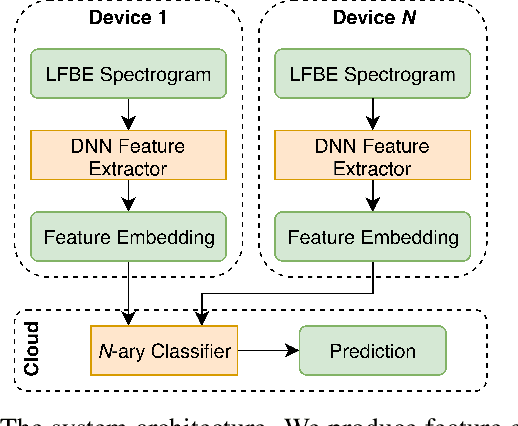
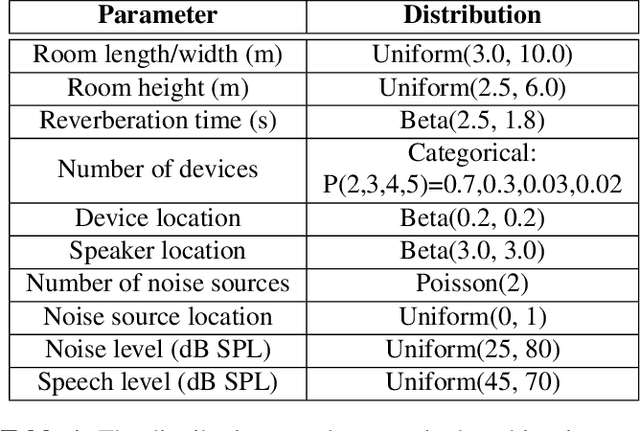
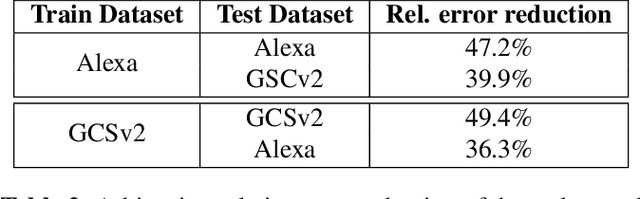
We introduce a variant of the speaker localization problem, which we call device arbitration. In the device arbitration problem, a user utters a keyword that is detected by multiple distributed microphone arrays (smart home devices), and we want to determine which device was closest to the user. Rather than solving the full localization problem, we propose an end-to-end machine learning system. This system learns a feature embedding that is computed independently on each device. The embeddings from each device are then aggregated together to produce the final arbitration decision. We use a large-scale room simulation to generate training and evaluation data, and compare our system against a signal processing baseline.

Joint Community Detection and Rotational Synchronization via Semidefinite Programming

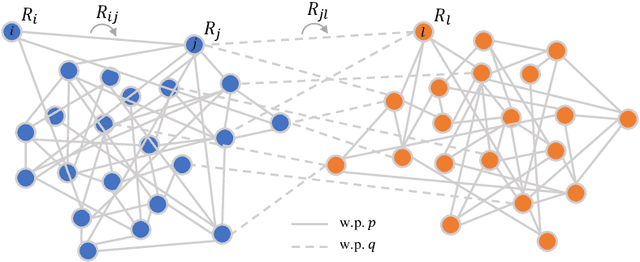
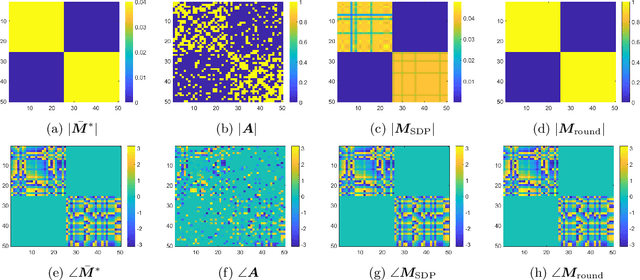
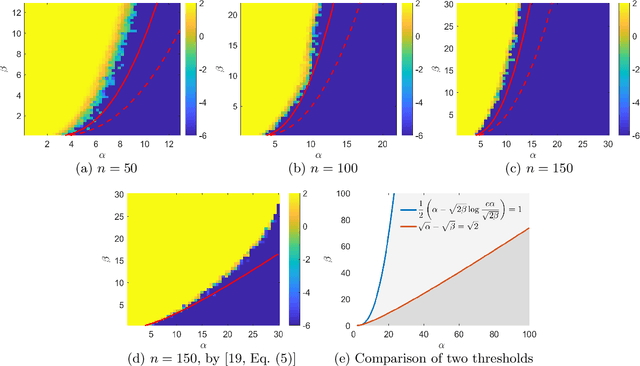
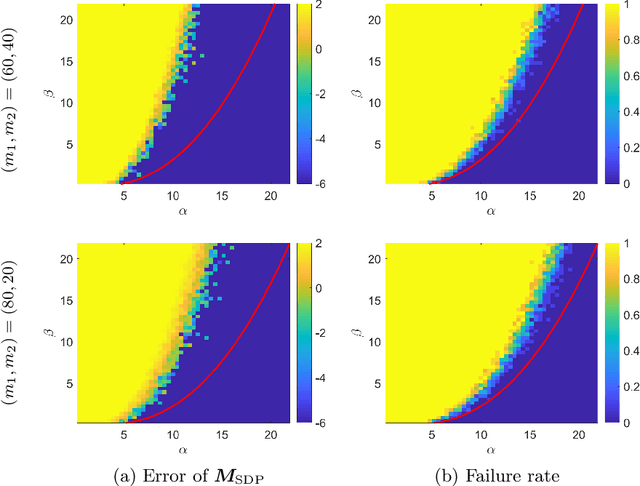
In the presence of heterogeneous data, where randomly rotated objects fall into multiple underlying categories, it is challenging to simultaneously classify them into clusters and synchronize them based on pairwise relations. This gives rise to the joint problem of community detection and synchronization. We propose a series of semidefinite relaxations, and prove their exact recovery when extending the celebrated stochastic block model to this new setting where both rotations and cluster identities are to be determined. Numerical experiments demonstrate the efficacy of our proposed algorithms and confirm our theoretical result which indicates a sharp phase transition for exact recovery.

Unsupervised Co-Learning on $\mathcal{G}$-Manifolds Across Irreducible Representations

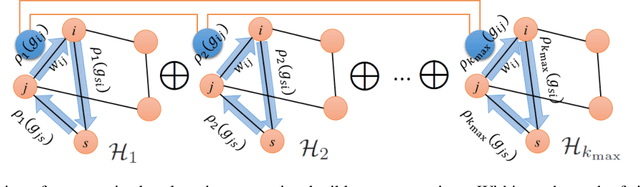
We introduce a novel co-learning paradigm for manifolds naturally equipped with a group action, motivated by recent developments on learning a manifold from attached fibre bundle structures. We utilize a representation theoretic mechanism that canonically associates multiple independent vector bundles over a common base manifold, which provides multiple views for the geometry of the underlying manifold. The consistency across these fibre bundles provide a common base for performing unsupervised manifold co-learning through the redundancy created artificially across irreducible representations of the transformation group. We demonstrate the efficacy of the proposed algorithmic paradigm through drastically improved robust nearest neighbor search and community detection on rotation-invariant cryo-electron microscopy image analysis.

Multi-Frequency Vector Diffusion Maps

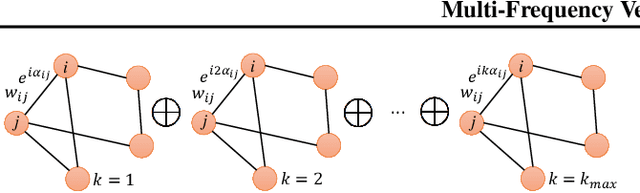
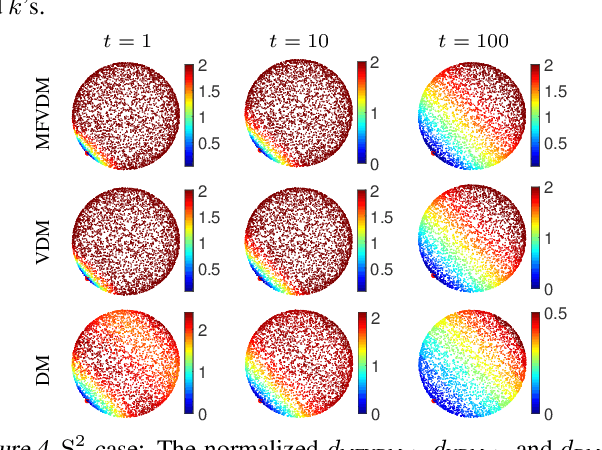
We introduce multi-frequency vector diffusion maps (MFVDM), a new framework for organizing and analyzing high dimensional datasets. The new method is a mathematical and algorithmic generalization of vector diffusion maps (VDM) and other non-linear dimensionality reduction methods. MFVDM combines different nonlinear embeddings of the data points defined with multiple unitary irreducible representations of the alignment group that connect two nodes in the graph. We illustrate the efficacy of MFVDM on synthetic data generated according to a random graph model and cryo-electron microscopy image dataset. The new method achieves better nearest neighbor search and alignment estimation than the state-of-the-arts VDM and diffusion maps (DM) on extremely noisy data.

Representation Theoretic Patterns in Multi-Frequency Class Averaging for Three-Dimensional Cryo-Electron Microscopy

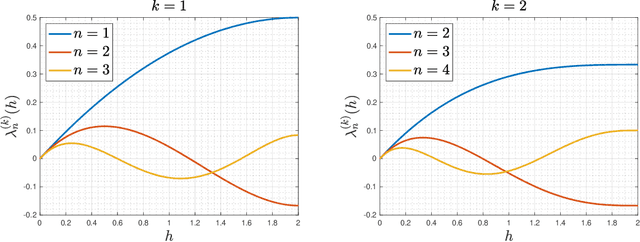
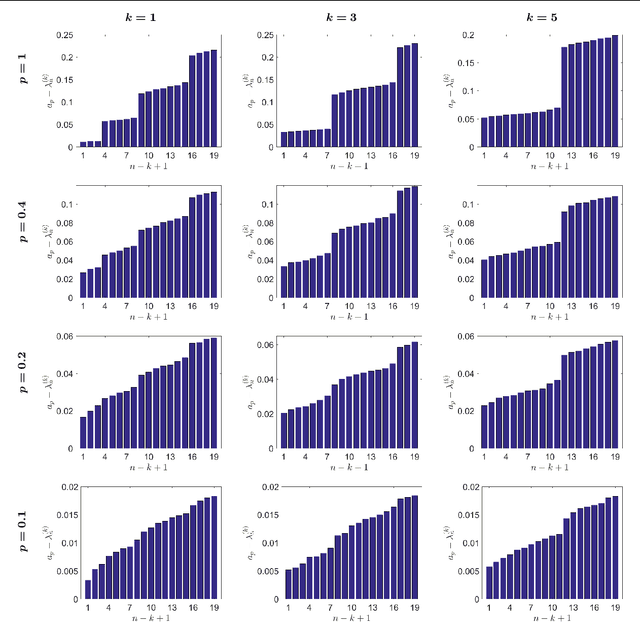
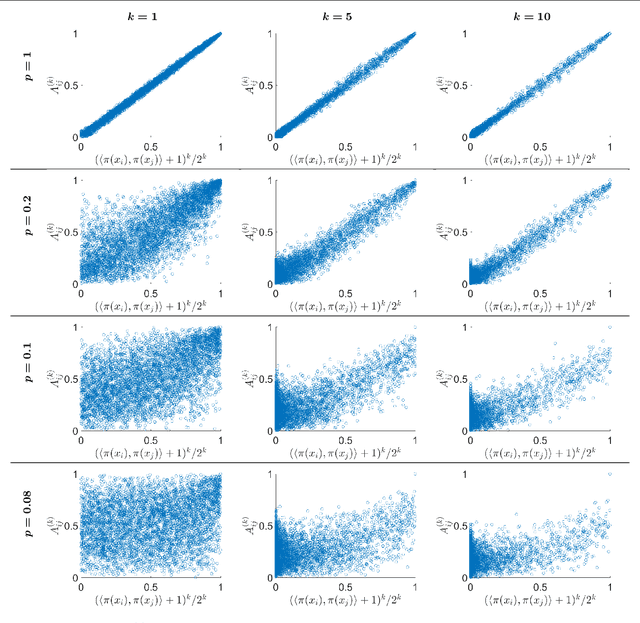
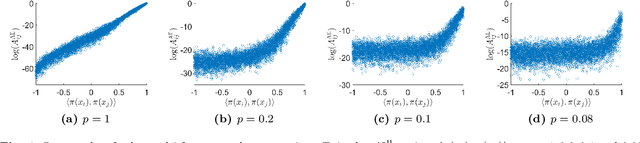
We develop in this paper a novel intrinsic classification algorithm -- multi-frequency class averaging (MFCA) -- for clustering noisy projection images obtained from three-dimensional cryo-electron microscopy (cryo-EM) by the similarity among their viewing directions. This new algorithm leverages multiple irreducible representations of the unitary group to introduce additional redundancy into the representation of the transport data, extending and outperforming the previous class averaging algorithm of Hadani and Singer [Foundations of Computational Mathematics, 11 (5), pp. 589--616 (2011)] that uses only a single representation. The formal algebraic model and representation theoretic patterns of the proposed MFCA algorithm extend the framework of Hadani and Singer to arbitrary irreducible representations of the unitary group. We conceptually establish the consistency and stability of MFCA by inspecting the spectral properties of a generalized localized parallel transport operator on the two-dimensional unit sphere through the lens of Wigner matrices. We demonstrate the efficacy of the proposed algorithm with numerical experiments.

Cryo-Electron Microscopy Image Analysis Using Multi-Frequency Vector Diffusion Maps

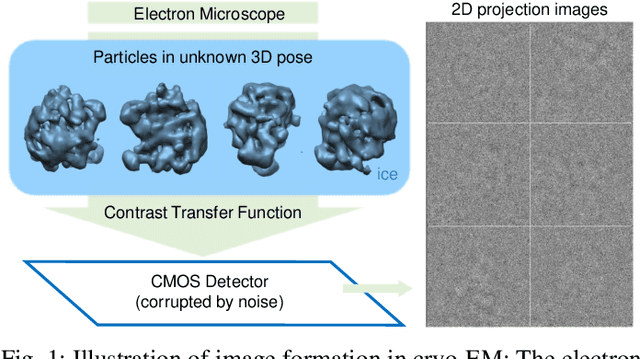
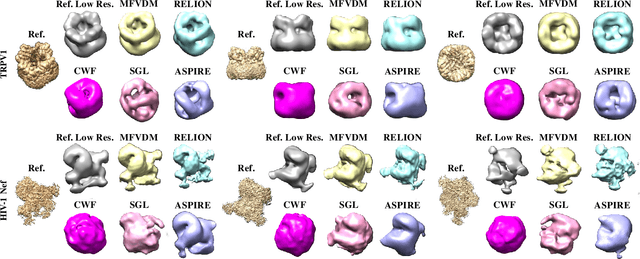
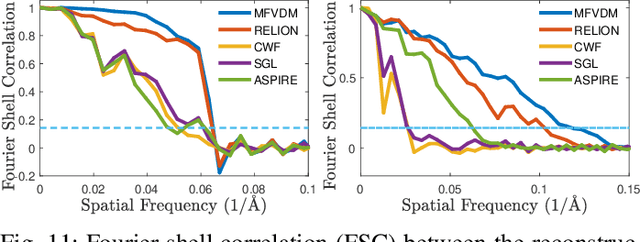
Cryo-electron microscopy (EM) single particle reconstruction is an entirely general technique for 3D structure determination of macromolecular complexes. However, because the images are taken at low electron dose, it is extremely hard to visualize the individual particle with low contrast and high noise level. In this paper, we propose a novel approach called multi-frequency vector diffusion maps (MFVDM) to improve the efficiency and accuracy of cryo-EM 2D image classification and denoising. This framework incorporates different irreducible representations of the estimated alignment between similar images. In addition, we propose a graph filtering scheme to denoise the images using the eigenvalues and eigenvectors of the MFVDM matrices. Through both simulated and publicly available real data, we demonstrate that our proposed method is efficient and robust to noise compared with the state-of-the-art cryo-EM 2D class averaging and image restoration algorithms.