Tingran Gao
Unsupervised Co-Learning on $\mathcal{G}$-Manifolds Across Irreducible Representations
Jun 29, 2019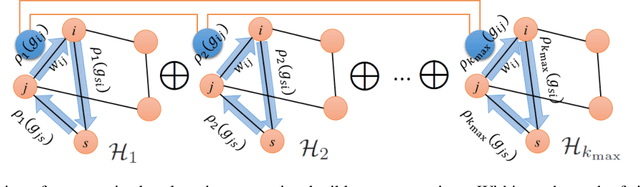
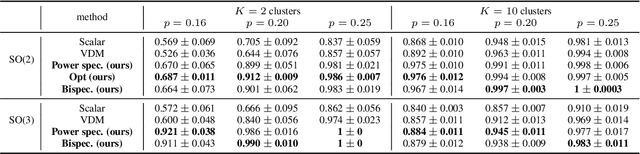


Abstract:We introduce a novel co-learning paradigm for manifolds naturally equipped with a group action, motivated by recent developments on learning a manifold from attached fibre bundle structures. We utilize a representation theoretic mechanism that canonically associates multiple independent vector bundles over a common base manifold, which provides multiple views for the geometry of the underlying manifold. The consistency across these fibre bundles provide a common base for performing unsupervised manifold co-learning through the redundancy created artificially across irreducible representations of the transformation group. We demonstrate the efficacy of the proposed algorithmic paradigm through drastically improved robust nearest neighbor search and community detection on rotation-invariant cryo-electron microscopy image analysis.
Representation Theoretic Patterns in Multi-Frequency Class Averaging for Three-Dimensional Cryo-Electron Microscopy
May 31, 2019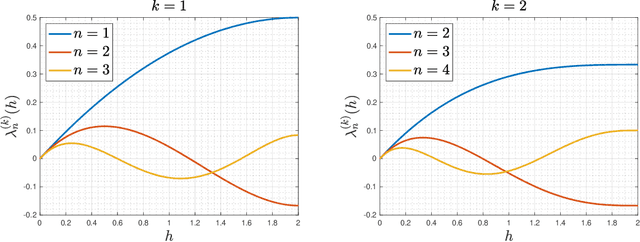
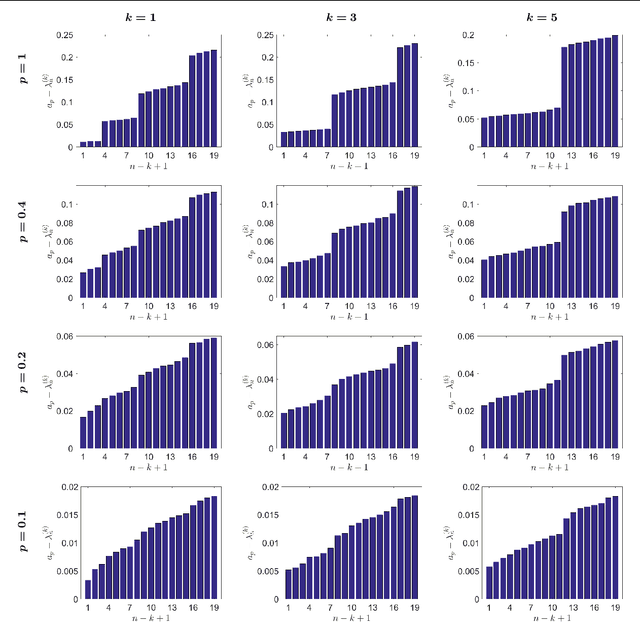
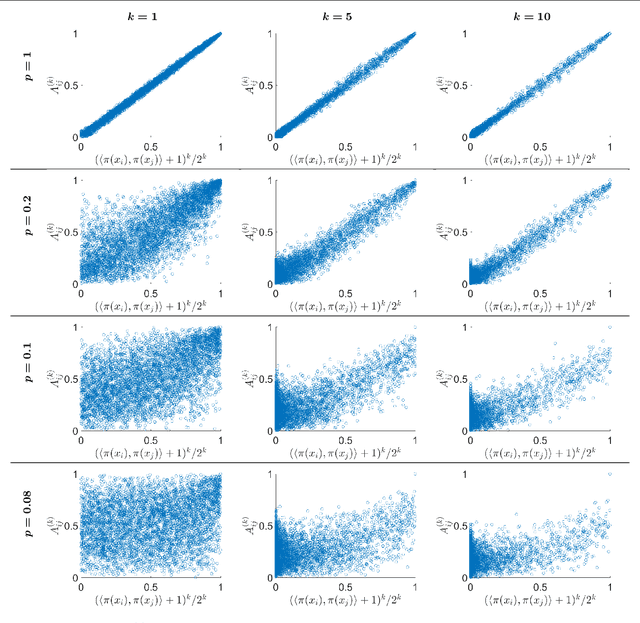
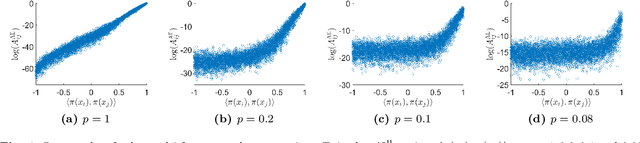
Abstract:We develop in this paper a novel intrinsic classification algorithm -- multi-frequency class averaging (MFCA) -- for clustering noisy projection images obtained from three-dimensional cryo-electron microscopy (cryo-EM) by the similarity among their viewing directions. This new algorithm leverages multiple irreducible representations of the unitary group to introduce additional redundancy into the representation of the transport data, extending and outperforming the previous class averaging algorithm of Hadani and Singer [Foundations of Computational Mathematics, 11 (5), pp. 589--616 (2011)] that uses only a single representation. The formal algebraic model and representation theoretic patterns of the proposed MFCA algorithm extend the framework of Hadani and Singer to arbitrary irreducible representations of the unitary group. We conceptually establish the consistency and stability of MFCA by inspecting the spectral properties of a generalized localized parallel transport operator on the two-dimensional unit sphere through the lens of Wigner matrices. We demonstrate the efficacy of the proposed algorithm with numerical experiments.
SelectNet: Learning to Sample from the Wild for Imbalanced Data Training
May 23, 2019



Abstract:Supervised learning from training data with imbalanced class sizes, a commonly encountered scenario in real applications such as anomaly/fraud detection, has long been considered a significant challenge in machine learning. Motivated by recent progress in curriculum and self-paced learning, we propose to adopt a semi-supervised learning paradigm by training a deep neural network, referred to as SelectNet, to selectively add unlabelled data together with their predicted labels to the training dataset. Unlike existing techniques designed to tackle the difficulty in dealing with class imbalanced training data such as resampling, cost-sensitive learning, and margin-based learning, SelectNet provides an end-to-end approach for learning from important unlabelled data "in the wild" that most likely belong to the under-sampled classes in the training data, thus gradually mitigates the imbalance in the data used for training the classifier. We demonstrate the efficacy of SelectNet through extensive numerical experiments on standard datasets in computer vision.
Uniform-in-Time Weak Error Analysis for Stochastic Gradient Descent Algorithms via Diffusion Approximation
Feb 02, 2019

Abstract:Diffusion approximation provides weak approximation for stochastic gradient descent algorithms in a finite time horizon. In this paper, we introduce new tools motivated by the backward error analysis of numerical stochastic differential equations into the theoretical framework of diffusion approximation, extending the validity of the weak approximation from finite to infinite time horizon. The new techniques developed in this paper enable us to characterize the asymptotic behavior of constant-step-size SGD algorithms for strongly convex objective functions, a goal previously unreachable within the diffusion approximation framework. Our analysis builds upon a truncated formal power expansion of the solution of a stochastic modified equation arising from diffusion approximation, where the main technical ingredient is a uniform-in-time weak error bound controlling the long-term behavior of the expansion coefficient functions near the global minimum. We expect these new techniques to greatly expand the range of applicability of diffusion approximation to cover wider and deeper aspects of stochastic optimization algorithms in data science.
Wasserstein Soft Label Propagation on Hypergraphs: Algorithm and Generalization Error Bounds
Sep 06, 2018

Abstract:Inspired by recent interests of developing machine learning and data mining algorithms on hypergraphs, we investigate in this paper the semi-supervised learning algorithm of propagating "soft labels" (e.g. probability distributions, class membership scores) over hypergraphs, by means of optimal transportation. Borrowing insights from Wasserstein propagation on graphs [Solomon et al. 2014], we re-formulate the label propagation procedure as a message-passing algorithm, which renders itself naturally to a generalization applicable to hypergraphs through Wasserstein barycenters. Furthermore, in a PAC learning framework, we provide generalization error bounds for propagating one-dimensional distributions on graphs and hypergraphs using 2-Wasserstein distance, by establishing the \textit{algorithmic stability} of the proposed semi-supervised learning algorithm. These theoretical results also shed new lights upon deeper understandings of the Wasserstein propagation on graphs.
Gaussian Process Landmarking on Manifolds
Jul 28, 2018


Abstract:As a means of improving analysis of biological shapes, we propose an algorithm for sampling a Riemannian manifold by sequentially selecting points with maximum uncertainty under a Gaussian process model. This greedy strategy is known to be near-optimal in the experimental design literature, and appears to outperform the use of user-placed landmarks in representing the geometry of biological objects in our application. In the noiseless regime, we establish an upper bound for the mean squared prediction error (MSPE) in terms of the number of samples and geometric quantities of the manifold, demonstrating that the MSPE for our proposed sequential design decays at a rate comparable to the oracle rate achievable by any sequential or non-sequential optimal design; to our knowledge this is the first result of this type for sequential experimental design. The key is to link the greedy algorithm to reduced basis methods in the context of model reduction for partial differential equations. We expect this approach will find additional applications in other fields of research.
Curvature of Hypergraphs via Multi-Marginal Optimal Transport
Mar 22, 2018

Abstract:We introduce a novel definition of curvature for hypergraphs, a natural generalization of graphs, by introducing a multi-marginal optimal transport problem for a naturally defined random walk on the hypergraph. This curvature, termed \emph{coarse scalar curvature}, generalizes a recent definition of Ricci curvature for Markov chains on metric spaces by Ollivier [Journal of Functional Analysis 256 (2009) 810-864], and is related to the scalar curvature when the hypergraph arises naturally from a Riemannian manifold. We investigate basic properties of the coarse scalar curvature and obtain several bounds. Empirical experiments indicate that coarse scalar curvatures are capable of detecting "bridges" across connected components in hypergraphs, suggesting it is an appropriate generalization of curvature on simple graphs.
A Tale of Two Bases: Local-Nonlocal Regularization on Image Patches with Convolution Framelets
Sep 12, 2016



Abstract:We propose an image representation scheme combining the local and nonlocal characterization of patches in an image. Our representation scheme can be shown to be equivalent to a tight frame constructed from convolving local bases (e.g. wavelet frames, discrete cosine transforms, etc.) with nonlocal bases (e.g. spectral basis induced by nonlinear dimension reduction on patches), and we call the resulting frame elements {\it convolution framelets}. Insight gained from analyzing the proposed representation leads to a novel interpretation of a recent high-performance patch-based image inpainting algorithm using Point Integral Method (PIM) and Low Dimension Manifold Model (LDMM) [Osher, Shi and Zhu, 2016]. In particular, we show that LDMM is a weighted $\ell_2$-regularization on the coefficients obtained by decomposing images into linear combinations of convolution framelets; based on this understanding, we extend the original LDMM to a reweighted version that yields further improved inpainting results. In addition, we establish the energy concentration property of convolution framelet coefficients for the setting where the local basis is constructed from a given nonlocal basis via a linear reconstruction framework; a generalization of this framework to unions of local embeddings can provide a natural setting for interpreting BM3D, one of the state-of-the-art image denoising algorithms.
Hypoelliptic Diffusion Maps I: Tangent Bundles
Mar 17, 2015



Abstract:We introduce the concept of Hypoelliptic Diffusion Maps (HDM), a framework generalizing Diffusion Maps in the context of manifold learning and dimensionality reduction. Standard non-linear dimensionality reduction methods (e.g., LLE, ISOMAP, Laplacian Eigenmaps, Diffusion Maps) focus on mining massive data sets using weighted affinity graphs; Orientable Diffusion Maps and Vector Diffusion Maps enrich these graphs by attaching to each node also some local geometry. HDM likewise considers a scenario where each node possesses additional structure, which is now itself of interest to investigate. Virtually, HDM augments the original data set with attached structures, and provides tools for studying and organizing the augmented ensemble. The goal is to obtain information on individual structures attached to the nodes and on the relationship between structures attached to nearby nodes, so as to study the underlying manifold from which the nodes are sampled. In this paper, we analyze HDM on tangent bundles, revealing its intimate connection with sub-Riemannian geometry and a family of hypoelliptic differential operators. In a later paper, we shall consider more general fibre bundles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge