Jian-Guo Liu
A personalized Uncertainty Quantification framework for patient survival models: estimating individual uncertainty of patients with metastatic brain tumors in the absence of ground truth
Nov 28, 2023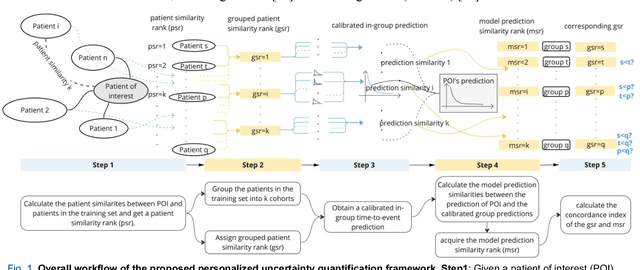
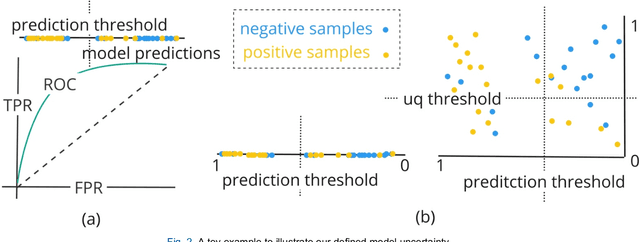
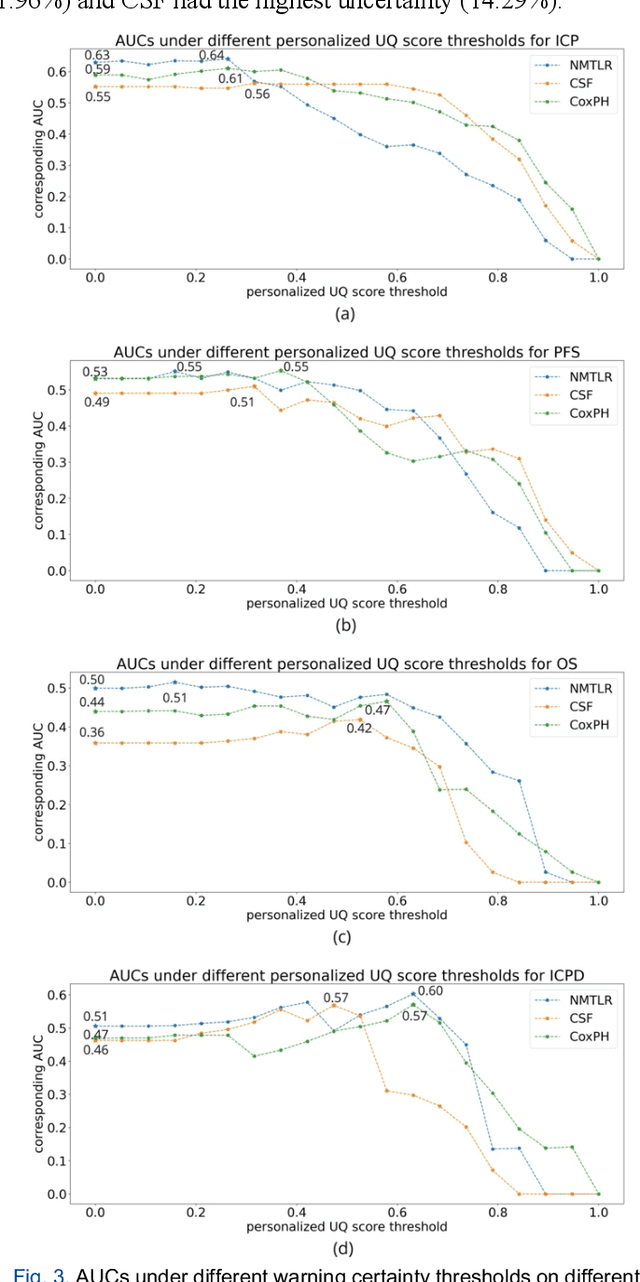
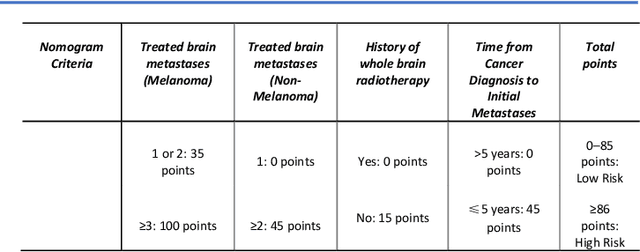
Abstract:TodevelopanovelUncertaintyQuantification (UQ) framework to estimate the uncertainty of patient survival models in the absence of ground truth, we developed and evaluated our approach based on a dataset of 1383 patients treated with stereotactic radiosurgery (SRS) for brain metastases between January 2015 and December 2020. Our motivating hypothesis is that a time-to-event prediction of a test patient on inference is more certain given a higher feature-space-similarity to patients in the training set. Therefore, the uncertainty for a particular patient-of-interest is represented by the concordance index between a patient similarity rank and a prediction similarity rank. Model uncertainty was defined as the increased percentage of the max uncertainty-constrained-AUC compared to the model AUC. We evaluated our method on multiple clinically-relevant endpoints, including time to intracranial progression (ICP), progression-free survival (PFS) after SRS, overall survival (OS), and time to ICP and/or death (ICPD), on a variety of both statistical and non-statistical models, including CoxPH, conditional survival forest (CSF), and neural multi-task linear regression (NMTLR). Our results show that all models had the lowest uncertainty on ICP (2.21%) and the highest uncertainty (17.28%) on ICPD. OS models demonstrated high variation in uncertainty performance, where NMTLR had the lowest uncertainty(1.96%)and CSF had the highest uncertainty (14.29%). In conclusion, our method can estimate the uncertainty of individual patient survival modeling results. As expected, our data empirically demonstrate that as model uncertainty measured via our technique increases, the similarity between a feature-space and its predicted outcome decreases.
Geometric ergodicity of SGLD via reflection coupling
Jan 17, 2023Abstract:We consider the geometric ergodicity of the Stochastic Gradient Langevin Dynamics (SGLD) algorithm under nonconvexity settings. Via the technique of reflection coupling, we prove the Wasserstein contraction of SGLD when the target distribution is log-concave only outside some compact set. The time discretization and the minibatch in SGLD introduce several difficulties when applying the reflection coupling, which are addressed by a series of careful estimates of conditional expectations. As a direct corollary, the SGLD with constant step size has an invariant distribution and we are able to obtain its geometric ergodicity in terms of $W_1$ distance. The generalization to non-gradient drifts is also included.
Data-driven Efficient Solvers and Predictions of Conformational Transitions for Langevin Dynamics on Manifold in High Dimensions
May 22, 2020



Abstract:We work on dynamic problems with collected data $\{\mathsf{x}_i\}$ that distributed on a manifold $\mathcal{M}\subset\mathbb{R}^p$. Through the diffusion map, we first learn the reaction coordinates $\{\mathsf{y}_i\}\subset \mathcal{N}$ where $\mathcal{N}$ is a manifold isometrically embedded into an Euclidean space $\mathbb{R}^\ell$ for $\ell \ll p$. The reaction coordinates enable us to obtain an efficient approximation for the dynamics described by a Fokker-Planck equation on the manifold $\mathcal{N}$. By using the reaction coordinates, we propose an implementable, unconditionally stable, data-driven upwind scheme which automatically incorporates the manifold structure of $\mathcal{N}$. Furthermore, we provide a weighted $L^2$ convergence analysis of the upwind scheme to the Fokker-Planck equation. The proposed upwind scheme leads to a Markov chain with transition probability between the nearest neighbor points. We can benefit from such property to directly conduct manifold-related computations such as finding the optimal coarse-grained network and the minimal energy path that represents chemical reactions or conformational changes. To establish the Fokker-Planck equation, we need to acquire information about the equilibrium potential of the physical system on $\mathcal{N}$. Hence, we apply a Gaussian Process regression algorithm to generate equilibrium potential for a new physical system with new parameters. Combining with the proposed upwind scheme, we can calculate the trajectory of the Fokker-Planck equation on $\mathcal{N}$ based on the generated equilibrium potential. Finally, we develop an algorithm to pullback the trajectory to the original high dimensional space as a generative data for the new physical system.
A stochastic version of Stein Variational Gradient Descent for efficient sampling
Apr 11, 2019



Abstract:We propose in this work RBM-SVGD, a stochastic version of Stein Variational Gradient Descent (SVGD) method for efficiently sampling from a given probability measure and thus useful for Bayesian inference. The method is to apply the Random Batch Method (RBM) for interacting particle systems proposed by Jin et al to the interacting particle systems in SVGD. While keeping the behaviors of SVGD, it reduces the computational cost, especially when the interacting kernel has long range. Numerical examples verify the efficiency of this new version of SVGD.
Uniform-in-Time Weak Error Analysis for Stochastic Gradient Descent Algorithms via Diffusion Approximation
Feb 02, 2019

Abstract:Diffusion approximation provides weak approximation for stochastic gradient descent algorithms in a finite time horizon. In this paper, we introduce new tools motivated by the backward error analysis of numerical stochastic differential equations into the theoretical framework of diffusion approximation, extending the validity of the weak approximation from finite to infinite time horizon. The new techniques developed in this paper enable us to characterize the asymptotic behavior of constant-step-size SGD algorithms for strongly convex objective functions, a goal previously unreachable within the diffusion approximation framework. Our analysis builds upon a truncated formal power expansion of the solution of a stochastic modified equation arising from diffusion approximation, where the main technical ingredient is a uniform-in-time weak error bound controlling the long-term behavior of the expansion coefficient functions near the global minimum. We expect these new techniques to greatly expand the range of applicability of diffusion approximation to cover wider and deeper aspects of stochastic optimization algorithms in data science.
On the diffusion approximation of nonconvex stochastic gradient descent
Mar 03, 2018



Abstract:We study the Stochastic Gradient Descent (SGD) method in nonconvex optimization problems from the point of view of approximating diffusion processes. We prove rigorously that the diffusion process can approximate the SGD algorithm weakly using the weak form of master equation for probability evolution. In the small step size regime and the presence of omnidirectional noise, our weak approximating diffusion process suggests the following dynamics for the SGD iteration starting from a local minimizer (resp.~saddle point): it escapes in a number of iterations exponentially (resp.~almost linearly) dependent on the inverse stepsize. The results are obtained using the theory for random perturbations of dynamical systems (theory of large deviations for local minimizers and theory of exiting for unstable stationary points). In addition, we discuss the effects of batch size for the deep neural networks, and we find that small batch size is helpful for SGD algorithms to escape unstable stationary points and sharp minimizers. Our theory indicates that one should increase the batch size at later stage for the SGD to be trapped in flat minimizers for better generalization.
Improved Collaborative Filtering Algorithm via Information Transformation
Oct 14, 2009



Abstract:In this paper, we propose a spreading activation approach for collaborative filtering (SA-CF). By using the opinion spreading process, the similarity between any users can be obtained. The algorithm has remarkably higher accuracy than the standard collaborative filtering (CF) using Pearson correlation. Furthermore, we introduce a free parameter $\beta$ to regulate the contributions of objects to user-user correlations. The numerical results indicate that decreasing the influence of popular objects can further improve the algorithmic accuracy and personality. We argue that a better algorithm should simultaneously require less computation and generate higher accuracy. Accordingly, we further propose an algorithm involving only the top-$N$ similar neighbors for each target user, which has both less computational complexity and higher algorithmic accuracy.
* 5 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge