Multi-Frequency Vector Diffusion Maps
Paper and Code
Jun 06, 2019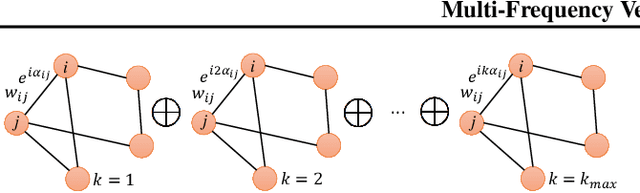


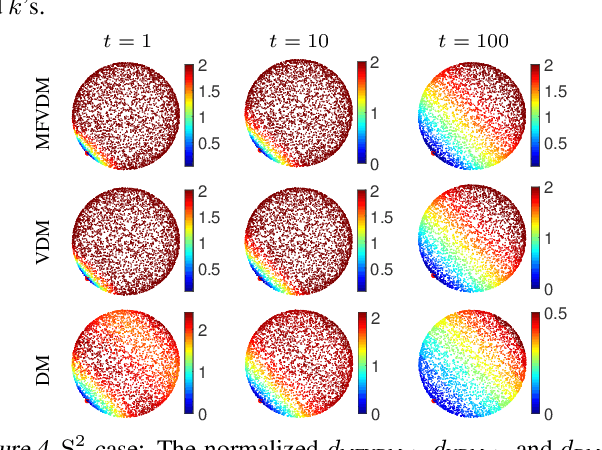
We introduce multi-frequency vector diffusion maps (MFVDM), a new framework for organizing and analyzing high dimensional datasets. The new method is a mathematical and algorithmic generalization of vector diffusion maps (VDM) and other non-linear dimensionality reduction methods. MFVDM combines different nonlinear embeddings of the data points defined with multiple unitary irreducible representations of the alignment group that connect two nodes in the graph. We illustrate the efficacy of MFVDM on synthetic data generated according to a random graph model and cryo-electron microscopy image dataset. The new method achieves better nearest neighbor search and alignment estimation than the state-of-the-arts VDM and diffusion maps (DM) on extremely noisy data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge