Improving the Robustness of 3D Human Pose Estimation: A Benchmark and Learning from Noisy Input

Despite the promising performance of current 3D human pose estimation techniques, understanding and enhancing their generalization on challenging in-the-wild videos remain an open problem. In this work, we focus on the robustness of 2D-to-3D pose lifters. To this end, we develop two benchmark datasets, namely Human3.6M-C and HumanEva-I-C, to examine the robustness of video-based 3D pose lifters to a wide range of common video corruptions including temporary occlusion, motion blur, and pixel-level noise. We observe the poor generalization of state-of-the-art 3D pose lifters in the presence of corruption and establish two techniques to tackle this issue. First, we introduce Temporal Additive Gaussian Noise (TAGN) as a simple yet effective 2D input pose data augmentation. Additionally, to incorporate the confidence scores output by the 2D pose detectors, we design a confidence-aware convolution (CA-Conv) block. Extensively tested on corrupted videos, the proposed strategies consistently boost the robustness of 3D pose lifters and serve as new baselines for future research.

Orthogonal Matrix Retrieval with Spatial Consensus for 3D Unknown-View Tomography

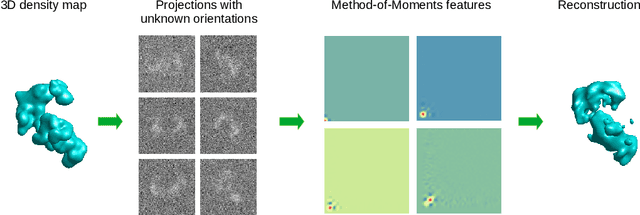
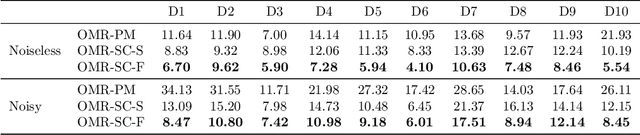
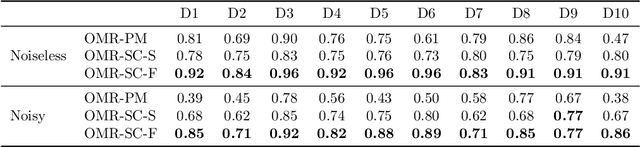
Unknown-view tomography (UVT) reconstructs a 3D density map from its 2D projections at unknown, random orientations. A line of work starting with Kam (1980) employs the method of moments (MoM) with rotation-invariant Fourier features to solve UVT in the frequency domain, assuming that the orientations are uniformly distributed. This line of work includes the recent orthogonal matrix retrieval (OMR) approaches based on matrix factorization, which, while elegant, either require side information about the density that is not available, or fail to be sufficiently robust. In order for OMR to break free from those restrictions, we propose to jointly recover the density map and the orthogonal matrices by requiring that they be mutually consistent. We regularize the resulting non-convex optimization problem by a denoised reference projection and a nonnegativity constraint. This is enabled by the new closed-form expressions for spatial autocorrelation features. Further, we design an easy-to-compute initial density map which effectively mitigates the non-convexity of the reconstruction problem. Experimental results show that the proposed OMR with spatial consensus is more robust and performs significantly better than the previous state-of-the-art OMR approach in the typical low-SNR scenario of 3D UVT.

Towards a Comprehensive Solution for a Vision-based Digitized Neurological Examination

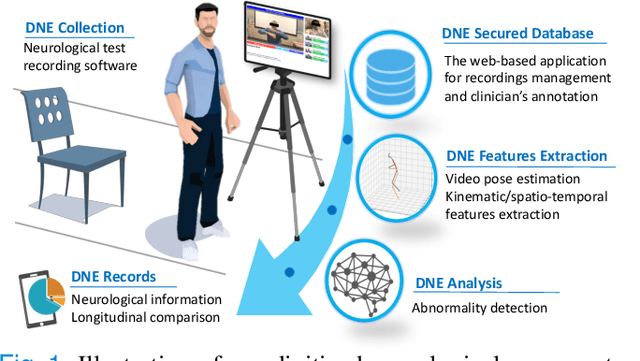
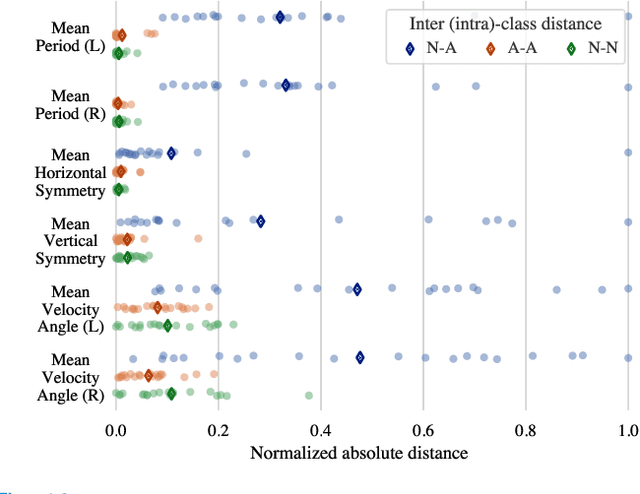
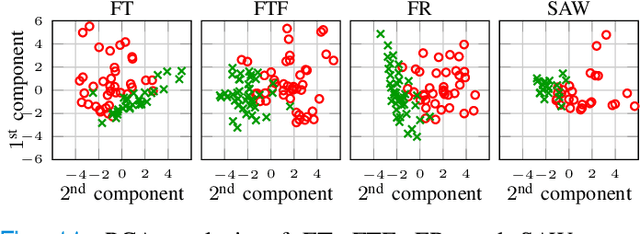
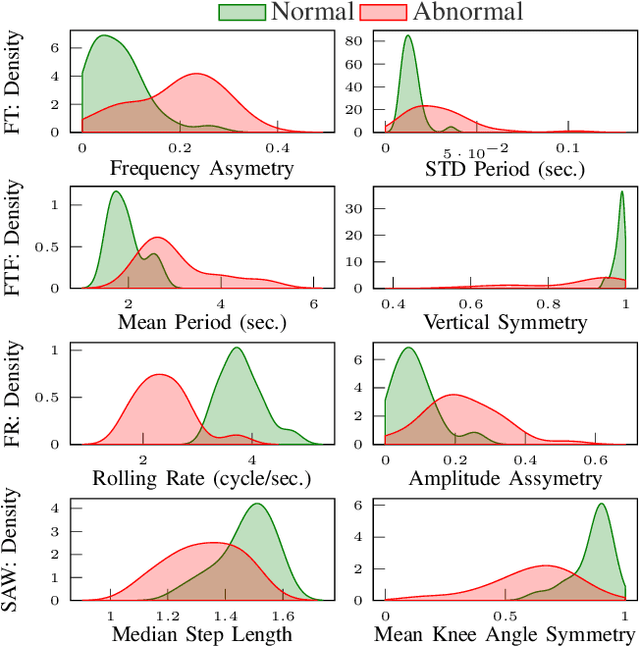
The ability to use digitally recorded and quantified neurological exam information is important to help healthcare systems deliver better care, in-person and via telehealth, as they compensate for a growing shortage of neurologists. Current neurological digital biomarker pipelines, however, are narrowed down to a specific neurological exam component or applied for assessing specific conditions. In this paper, we propose an accessible vision-based exam and documentation solution called Digitized Neurological Examination (DNE) to expand exam biomarker recording options and clinical applications using a smartphone/tablet. Through our DNE software, healthcare providers in clinical settings and people at home are enabled to video capture an examination while performing instructed neurological tests, including finger tapping, finger to finger, forearm roll, and stand-up and walk. Our modular design of the DNE software supports integrations of additional tests. The DNE extracts from the recorded examinations the 2D/3D human-body pose and quantifies kinematic and spatio-temporal features. The features are clinically relevant and allow clinicians to document and observe the quantified movements and the changes of these metrics over time. A web server and a user interface for recordings viewing and feature visualizations are available. DNE was evaluated on a collected dataset of 21 subjects containing normal and simulated-impaired movements. The overall accuracy of DNE is demonstrated by classifying the recorded movements using various machine learning models. Our tests show an accuracy beyond 90% for upper-limb tests and 80% for the stand-up and walk tests.

An Adversarial Learning Based Approach for Unknown View Tomographic Reconstruction

The goal of 2D tomographic reconstruction is to recover an image given its projection lines from various views. It is often presumed that projection angles associated with the projection lines are known in advance. Under certain situations, however, these angles are known only approximately or are completely unknown. It becomes more challenging to reconstruct the image from a collection of random projection lines. We propose an adversarial learning based approach to recover the image and the projection angle distribution by matching the empirical distribution of the measurements with the generated data. Fitting the distributions is achieved through solving a min-max game between a generator and a critic based on Wasserstein generative adversarial network structure. To accommodate the update of the projection angle distribution through gradient back propagation, we approximate the loss using the Gumbel-Softmax reparameterization of samples from discrete distributions. Our theoretical analysis verifies the unique recovery of the image and the projection distribution up to a rotation and reflection upon convergence. Our extensive numerical experiments showcase the potential of our method to accurately recover the image and the projection angle distribution under noise contamination.

Joint Learning of Portrait Intrinsic Decomposition and Relighting

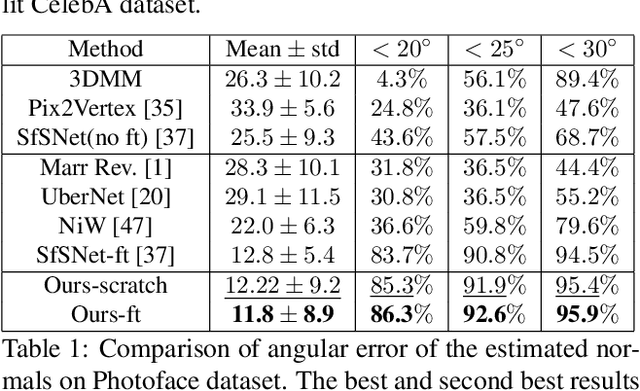
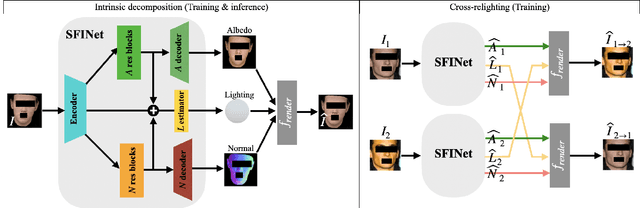
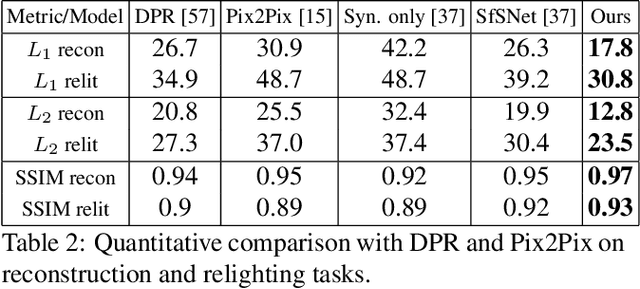
Inverse rendering is the problem of decomposing an image into its intrinsic components, i.e. albedo, normal and lighting. To solve this ill-posed problem from single image, state-of-the-art methods in shape from shading mostly resort to supervised training on all the components on either synthetic or real datasets. Here, we propose a new self-supervised training paradigm that 1) reduces the need for full supervision on the decomposition task and 2) takes into account the relighting task. We introduce new self-supervised loss terms that leverage the consistencies between multi-lit images (images of the same scene under different illuminations). Our approach is applicable to multi-lit datasets. We apply our training approach in two settings: 1) train on a mixture of synthetic and real data, 2) train on real datasets with limited supervision. We show-case the effectiveness of our training paradigm on both intrinsic decomposition and relighting and demonstrate how the model struggles in both tasks without the self-supervised loss terms in limited supervision settings. We provide results of comprehensive experiments on SfSNet, CelebA and Photoface datasets and verify the performance of our approach on images in the wild.

DeepQAMVS: Query-Aware Hierarchical Pointer Networks for Multi-Video Summarization

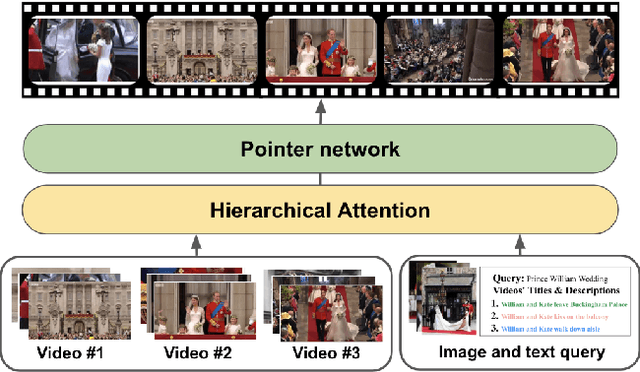
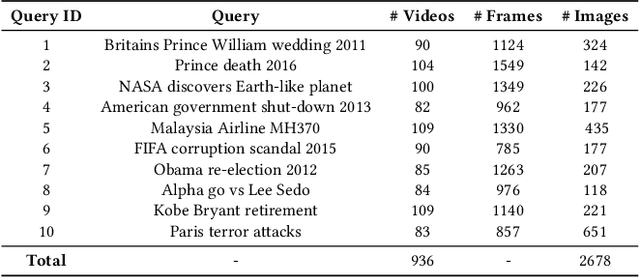
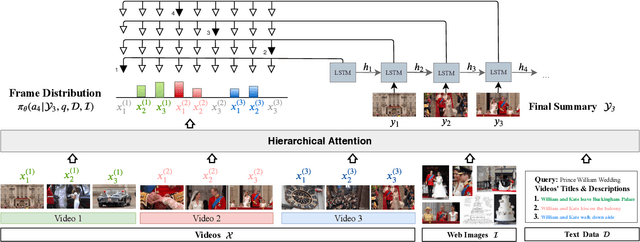
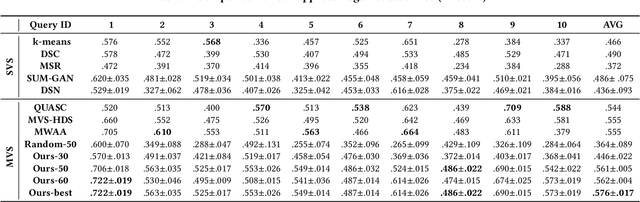
The recent growth of web video sharing platforms has increased the demand for systems that can efficiently browse, retrieve and summarize video content. Query-aware multi-video summarization is a promising technique that caters to this demand. In this work, we introduce a novel Query-Aware Hierarchical Pointer Network for Multi-Video Summarization, termed DeepQAMVS, that jointly optimizes multiple criteria: (1) conciseness, (2) representativeness of important query-relevant events and (3) chronological soundness. We design a hierarchical attention model that factorizes over three distributions, each collecting evidence from a different modality, followed by a pointer network that selects frames to include in the summary. DeepQAMVS is trained with reinforcement learning, incorporating rewards that capture representativeness, diversity, query-adaptability and temporal coherence. We achieve state-of-the-art results on the MVS1K dataset, with inference time scaling linearly with the number of input video frames.

MSR-GAN: Multi-Segment Reconstruction via Adversarial Learning

Multi-segment reconstruction (MSR) is the problem of estimating a signal given noisy partial observations. Here each observation corresponds to a randomly located segment of the signal. While previous works address this problem using template or moment-matching, in this paper we address MSR from an unsupervised adversarial learning standpoint, named MSR-GAN. We formulate MSR as a distribution matching problem where the goal is to recover the signal and the probability distribution of the segments such that the distribution of the generated measurements following a known forward model is close to the real observations. This is achieved once a min-max optimization involving a generator-discriminator pair is solved. MSR-GAN is mainly inspired by CryoGAN [1]. However, in MSR-GAN we no longer assume the probability distribution of the latent variables, i.e. segment locations, is given and seek to recover it alongside the unknown signal. For this purpose, we show that the loss at the generator side originally is non-differentiable with respect to the segment distribution. Thus, we propose to approximate it using Gumbel-Softmax reparametrization trick. Our proposed solution is generalizable to a wide range of inverse problems. Our simulation results and comparison with various baselines verify the potential of our approach in different settings.

UVTomo-GAN: An adversarial learning based approach for unknown view X-ray tomographic reconstruction

Tomographic reconstruction recovers an unknown image given its projections from different angles. State-of-the-art methods addressing this problem assume the angles associated with the projections are known a-priori. Given this knowledge, the reconstruction process is straightforward as it can be formulated as a convex problem. Here, we tackle a more challenging setting: 1) the projection angles are unknown, 2) they are drawn from an unknown probability distribution. In this set-up our goal is to recover the image and the projection angle distribution using an unsupervised adversarial learning approach. For this purpose, we formulate the problem as a distribution matching between the real projection lines and the generated ones from the estimated image and projection distribution. This is then solved by reaching the equilibrium in a min-max game between a generator and a discriminator. Our novel contribution is to recover the unknown projection distribution and the image simultaneously using adversarial learning. To accommodate this, we use Gumbel-softmax approximation of samples from categorical distribution to approximate the generator's loss as a function of the unknown image and the projection distribution. Our approach can be generalized to different inverse problems. Our simulation results reveal the ability of our method in successfully recovering the image and the projection distribution in various settings.