Convergence Rates for Deterministic and Stochastic Subgradient Methods Without Lipschitz Continuity
Paper and Code
Feb 26, 2018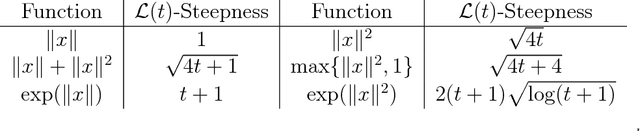
We extend the classic convergence rate theory for subgradient methods to apply to non-Lipschitz functions. For the deterministic projected subgradient method, we present a global $O(1/\sqrt{T})$ convergence rate for any convex function which is locally Lipschitz around its minimizers. This approach is based on Shor's classic subgradient analysis and implies generalizations of the standard convergence rates for gradient descent on functions with Lipschitz or H\"older continuous gradients. Further, we show a $O(1/\sqrt{T})$ convergence rate for the stochastic projected subgradient method on convex functions with at most quadratic growth, which improves to $O(1/T)$ under either strong convexity or a weaker quadratic lower bound condition.
* Update 2/26/18: Major revision improving the convergence results to
no longer need an exponential upper bound on function growth in the convex
case. Now local Lipschitz continuity around a minimizer suffices for a global
convergence rate. Update 12/21/17: Added three more references on weakening
strong convexity and minorly changed some wording. 16 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge