The Best of Many Worlds: Dual Mirror Descent for Online Allocation Problems
Paper and Code
Nov 18, 2020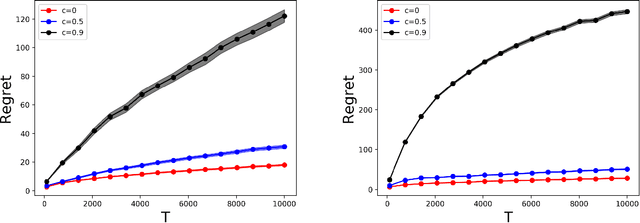
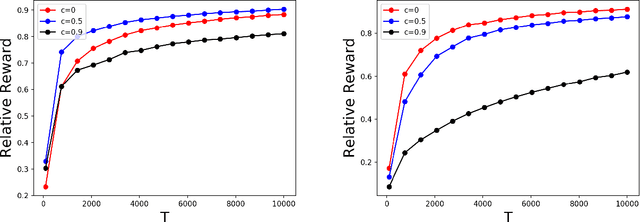
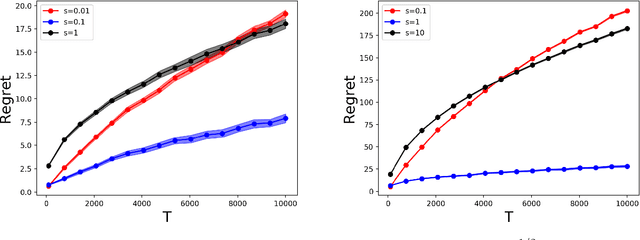
Online allocation problems with resource constraints are central problems in revenue management and online advertising. In these problems, requests arrive sequentially during a finite horizon and, for each request, a decision maker needs to choose an action that consumes a certain amount of resources and generates reward. The objective is to maximize cumulative rewards subject to a constraint on the total consumption of resources. In this paper, we consider a data-driven setting in which the reward and resource consumption of each request are generated using an input model that is unknown to the decision maker. We design a general class of algorithms that attain good performance in various inputs models without knowing which type of input they are facing. In particular, our algorithms are asymptotically optimal under stochastic i.i.d. input model as well as various non-stationary stochastic input models, and they attain an asymptotically optimal fixed competitive ratio when the input is adversarial. Our algorithms operate in the Lagrangian dual space: they maintain a dual multiplier for each resource that is updated using online mirror descent. By choosing the reference function accordingly, we recover dual sub-gradient descent and dual exponential weights algorithm. The resulting algorithms are simple, fast, and have minimal requirements on the reward functions, consumption functions and the action space, in contrast to existing methods for online allocation problems. We discuss applications to network revenue management, online bidding in repeated auctions with budget constraints, online proportional matching with high entropy, and personalized assortment optimization with limited inventories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge