Robust Budget Pacing with a Single Sample

Major Internet advertising platforms offer budget pacing tools as a standard service for advertisers to manage their ad campaigns. Given the inherent non-stationarity in an advertiser's value and also competing advertisers' values over time, a commonly used approach is to learn a target expenditure plan that specifies a target spend as a function of time, and then run a controller that tracks this plan. This raises the question: how many historical samples are required to learn a good expenditure plan? We study this question by considering an advertiser repeatedly participating in $T$ second-price auctions, where the tuple of her value and the highest competing bid is drawn from an unknown time-varying distribution. The advertiser seeks to maximize her total utility subject to her budget constraint. Prior work has shown the sufficiency of $T\log T$ samples per distribution to achieve the optimal $O(\sqrt{T})$-regret. We dramatically improve this state-of-the-art and show that just one sample per distribution is enough to achieve the near-optimal $\tilde O(\sqrt{T})$-regret, while still being robust to noise in the sampling distributions.

Online Resource Allocation under Horizon Uncertainty

We study stochastic online resource allocation: a decision maker needs to allocate limited resources to stochastically-generated sequentially-arriving requests in order to maximize reward. Motivated by practice, we consider a data-driven setting in which requests are drawn independently from a distribution that is unknown to the decision maker. Online resource allocation and its special cases have been studied extensively in the past, but these previous results crucially and universally rely on a practically-untenable assumption: the total number of requests (the horizon) is known to the decision maker in advance. In many applications, such as revenue management and online advertising, the number of requests can vary widely because of fluctuations in demand or user traffic intensity. In this work, we develop online algorithms that are robust to horizon uncertainty. In sharp contrast to the known-horizon setting, we show that no algorithm can achieve a constant asymptotic competitive ratio that is independent of the horizon uncertainty. We then introduce a novel algorithm that combines dual mirror descent with a carefully-chosen target consumption sequence and prove that it achieves a bounded competitive ratio. Our algorithm is near-optimal in the sense that its competitive ratio attains the optimal rate of growth when the horizon uncertainty grows large.

Single-Leg Revenue Management with Advice

Single-leg revenue management is a foundational problem of revenue management that has been particularly impactful in the airline and hotel industry: Given $n$ units of a resource, e.g. flight seats, and a stream of sequentially-arriving customers segmented by fares, what is the optimal online policy for allocating the resource. Previous work focused on designing algorithms when forecasts are available, which are not robust to inaccuracies in the forecast, or online algorithms with worst-case performance guarantees, which can be too conservative in practice. In this work, we look at the single-leg revenue management problem through the lens of the algorithms-with-advice framework, which attempts to optimally incorporate advice/predictions about the future into online algorithms. In particular, we characterize the Pareto frontier that captures the tradeoff between consistency (performance when advice is accurate) and competitiveness (performance when advice is inaccurate) for every advice. Moreover, we provide an online algorithm that always achieves performance on this Pareto frontier. We also study the class of protection level policies, which is the most widely-deployed technique for single-leg revenue management: we provide an algorithm to incorporate advice into protection levels that optimally trades off consistency and competitiveness. Moreover, we empirically evaluate the performance of these algorithms on synthetic data. We find that our algorithm for protection level policies performs remarkably well on most instances, even if it is not guaranteed to be on the Pareto frontier in theory.

The Best of Many Worlds: Dual Mirror Descent for Online Allocation Problems

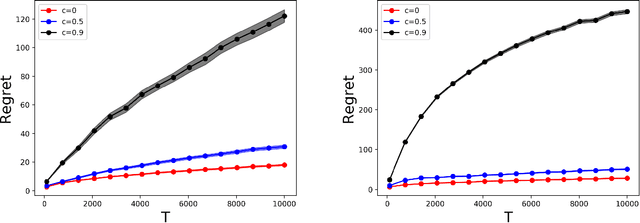
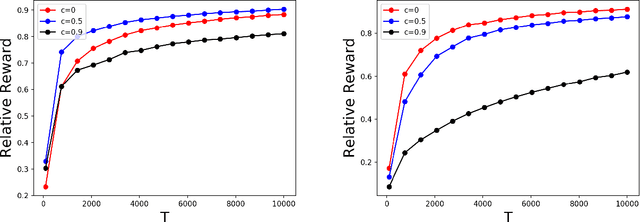
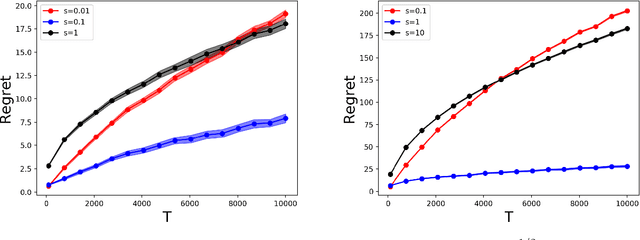
Online allocation problems with resource constraints are central problems in revenue management and online advertising. In these problems, requests arrive sequentially during a finite horizon and, for each request, a decision maker needs to choose an action that consumes a certain amount of resources and generates reward. The objective is to maximize cumulative rewards subject to a constraint on the total consumption of resources. In this paper, we consider a data-driven setting in which the reward and resource consumption of each request are generated using an input model that is unknown to the decision maker. We design a general class of algorithms that attain good performance in various inputs models without knowing which type of input they are facing. In particular, our algorithms are asymptotically optimal under stochastic i.i.d. input model as well as various non-stationary stochastic input models, and they attain an asymptotically optimal fixed competitive ratio when the input is adversarial. Our algorithms operate in the Lagrangian dual space: they maintain a dual multiplier for each resource that is updated using online mirror descent. By choosing the reference function accordingly, we recover dual sub-gradient descent and dual exponential weights algorithm. The resulting algorithms are simple, fast, and have minimal requirements on the reward functions, consumption functions and the action space, in contrast to existing methods for online allocation problems. We discuss applications to network revenue management, online bidding in repeated auctions with budget constraints, online proportional matching with high entropy, and personalized assortment optimization with limited inventories.

Regularized Online Allocation Problems: Fairness and Beyond

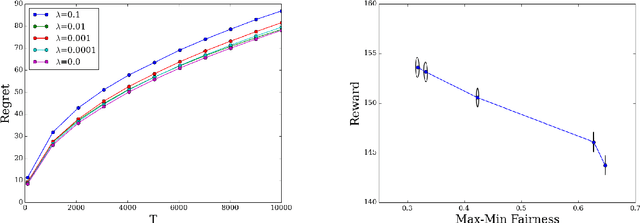
Online allocation problems with resource constraints have a rich history in computer science and operations research. In this paper, we introduce the \emph{regularized online allocation problem}, a variant that includes a non-linear regularizer acting on the total resource consumption. In this problem, requests repeatedly arrive over time and, for each request, a decision maker needs to take an action that generates a reward and consumes resources. The objective is to simultaneously maximize total rewards and the value of the regularizer subject to the resource constraints. Our primary motivation is the online allocation of internet advertisements wherein firms seek to maximize additive objectives such as the revenue or efficiency of the allocation. By introducing a regularizer, firms can account for the fairness of the allocation or, alternatively, punish under-delivery of advertisements---two common desiderata in internet advertising markets. We design an algorithm when arrivals are drawn independently from a distribution that is unknown to the decision maker. Our algorithm is simple, fast, and attains the optimal order of sub-linear regret compared to the optimal allocation with the benefit of hindsight. Numerical experiments confirm the effectiveness of the proposed algorithm and of the regularizers in an internet advertising application.

Contextual Bandits with Cross-learning

In the classical contextual bandits problem, in each round $t$, a learner observes some context $c$, chooses some action $a$ to perform, and receives some reward $r_{a,t}(c)$. We consider the variant of this problem where in addition to receiving the reward $r_{a,t}(c)$, the learner also learns the values of $r_{a,t}(c')$ for all other contexts $c'$; i.e., the rewards that would have been achieved by performing that action under different contexts. This variant arises in several strategic settings, such as learning how to bid in non-truthful repeated auctions (in this setting the context is the decision maker's private valuation for each auction). We call this problem the contextual bandits problem with cross-learning. The best algorithms for the classical contextual bandits problem achieve $\tilde{O}(\sqrt{CKT})$ regret against all stationary policies, where $C$ is the number of contexts, $K$ the number of actions, and $T$ the number of rounds. We demonstrate algorithms for the contextual bandits problem with cross-learning that remove the dependence on $C$ and achieve regret $O(\sqrt{KT})$ (when contexts are stochastic with known distribution), $\tilde{O}(K^{1/3}T^{2/3})$ (when contexts are stochastic with unknown distribution), and $\tilde{O}(\sqrt{KT})$ (when contexts are adversarial but rewards are stochastic).