Learning across Data Owners with Joint Differential Privacy

In this paper, we study the setting in which data owners train machine learning models collaboratively under a privacy notion called joint differential privacy [Kearns et al., 2018]. In this setting, the model trained for each data owner $j$ uses $j$'s data without privacy consideration and other owners' data with differential privacy guarantees. This setting was initiated in [Jain et al., 2021] with a focus on linear regressions. In this paper, we study this setting for stochastic convex optimization (SCO). We present an algorithm that is a variant of DP-SGD [Song et al., 2013; Abadi et al., 2016] and provides theoretical bounds on its population loss. We compare our algorithm to several baselines and discuss for what parameter setups our algorithm is more preferred. We also empirically study joint differential privacy in the multi-class classification problem over two public datasets. Our empirical findings are well-connected to the insights from our theoretical results.

Differentially-Private Hierarchical Clustering with Provable Approximation Guarantees

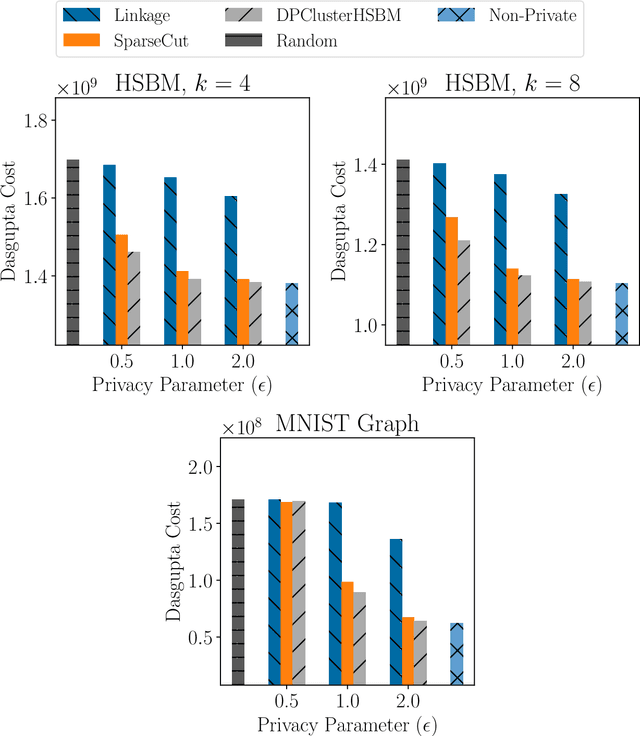
Hierarchical Clustering is a popular unsupervised machine learning method with decades of history and numerous applications. We initiate the study of differentially private approximation algorithms for hierarchical clustering under the rigorous framework introduced by (Dasgupta, 2016). We show strong lower bounds for the problem: that any $\epsilon$-DP algorithm must exhibit $O(|V|^2/ \epsilon)$-additive error for an input dataset $V$. Then, we exhibit a polynomial-time approximation algorithm with $O(|V|^{2.5}/ \epsilon)$-additive error, and an exponential-time algorithm that meets the lower bound. To overcome the lower bound, we focus on the stochastic block model, a popular model of graphs, and, with a separation assumption on the blocks, propose a private $1+o(1)$ approximation algorithm which also recovers the blocks exactly. Finally, we perform an empirical study of our algorithms and validate their performance.

Regret Minimization with Noisy Observations

In a typical optimization problem, the task is to pick one of a number of options with the lowest cost or the highest value. In practice, these cost/value quantities often come through processes such as measurement or machine learning, which are noisy, with quantifiable noise distributions. To take these noise distributions into account, one approach is to assume a prior for the values, use it to build a posterior, and then apply standard stochastic optimization to pick a solution. However, in many practical applications, such prior distributions may not be available. In this paper, we study such scenarios using a regret minimization model. In our model, the task is to pick the highest one out of $n$ values. The values are unknown and chosen by an adversary, but can be observed through noisy channels, where additive noises are stochastically drawn from known distributions. The goal is to minimize the regret of our selection, defined as the expected difference between the highest and the selected value on the worst-case choices of values. We show that the na\"ive algorithm of picking the highest observed value has regret arbitrarily worse than the optimum, even when $n = 2$ and the noises are unbiased in expectation. On the other hand, we propose an algorithm which gives a constant-approximation to the optimal regret for any $n$. Our algorithm is conceptually simple, computationally efficient, and requires only minimal knowledge of the noise distributions.

Optimal Approximation -- Smoothness Tradeoffs for Soft-Max Functions

A soft-max function has two main efficiency measures: (1) approximation - which corresponds to how well it approximates the maximum function, (2) smoothness - which shows how sensitive it is to changes of its input. Our goal is to identify the optimal approximation-smoothness tradeoffs for different measures of approximation and smoothness. This leads to novel soft-max functions, each of which is optimal for a different application. The most commonly used soft-max function, called exponential mechanism, has optimal tradeoff between approximation measured in terms of expected additive approximation and smoothness measured with respect to R\'enyi Divergence. We introduce a soft-max function, called "piecewise linear soft-max", with optimal tradeoff between approximation, measured in terms of worst-case additive approximation and smoothness, measured with respect to $\ell_q$-norm. The worst-case approximation guarantee of the piecewise linear mechanism enforces sparsity in the output of our soft-max function, a property that is known to be important in Machine Learning applications [Martins et al. '16, Laha et al. '18] and is not satisfied by the exponential mechanism. Moreover, the $\ell_q$-smoothness is suitable for applications in Mechanism Design and Game Theory where the piecewise linear mechanism outperforms the exponential mechanism. Finally, we investigate another soft-max function, called power mechanism, with optimal tradeoff between expected \textit{multiplicative} approximation and smoothness with respect to the R\'enyi Divergence, which provides improved theoretical and practical results in differentially private submodular optimization.

Fair Hierarchical Clustering

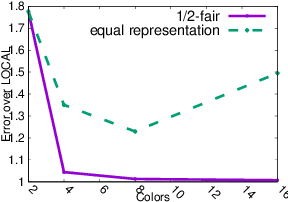
As machine learning has become more prevalent, researchers have begun to recognize the necessity of ensuring machine learning systems are fair. Recently, there has been an interest in defining a notion of fairness that mitigates over-representation in traditional clustering. In this paper we extend this notion to hierarchical clustering, where the goal is to recursively partition the data to optimize a specific objective. For various natural objectives, we obtain simple, efficient algorithms to find a provably good fair hierarchical clustering. Empirically, we show that our algorithms can find a fair hierarchical clustering, with only a negligible loss in the objective.

Fair Correlation Clustering

In this paper, we study correlation clustering under fairness constraints. Fair variants of $k$-median and $k$-center clustering have been studied recently, and approximation algorithms using a notion called fairlet decomposition have been proposed. We obtain approximation algorithms for fair correlation clustering under several important types of fairness constraints. Our results hinge on obtaining a fairlet decomposition for correlation clustering by introducing a novel combinatorial optimization problem. We define a fairlet decomposition with cost similar to the $k$-median cost and this allows us to obtain approximation algorithms for a wide range of fairness constraints. We complement our theoretical results with an in-depth analysis of our algorithms on real graphs where we show that fair solutions to correlation clustering can be obtained with limited increase in cost compared to the state-of-the-art (unfair) algorithms.

Clustering without Over-Representation

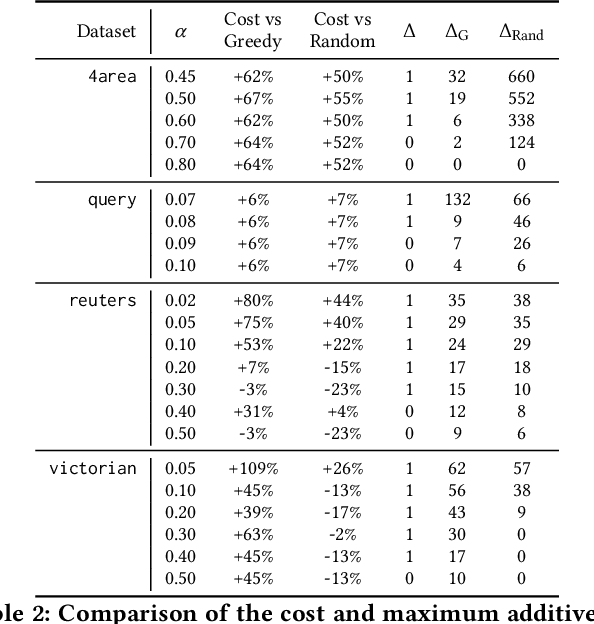
In this paper we consider clustering problems in which each point is endowed with a color. The goal is to cluster the points to minimize the classical clustering cost but with the additional constraint that no color is over-represented in any cluster. This problem is motivated by practical clustering settings, e.g., in clustering news articles where the color of an article is its source, it is preferable that no single news source dominates any cluster. For the most general version of this problem, we obtain an algorithm that has provable guarantees of performance; our algorithm is based on finding a fractional solution using a linear program and rounding the solution subsequently. For the special case of the problem where no color has an absolute majority in any cluster, we obtain a simpler combinatorial algorithm also with provable guarantees. Experiments on real-world data shows that our algorithms are effective in finding good clustering without over-representation.

Contextual Bandits with Cross-learning

In the classical contextual bandits problem, in each round $t$, a learner observes some context $c$, chooses some action $a$ to perform, and receives some reward $r_{a,t}(c)$. We consider the variant of this problem where in addition to receiving the reward $r_{a,t}(c)$, the learner also learns the values of $r_{a,t}(c')$ for all other contexts $c'$; i.e., the rewards that would have been achieved by performing that action under different contexts. This variant arises in several strategic settings, such as learning how to bid in non-truthful repeated auctions (in this setting the context is the decision maker's private valuation for each auction). We call this problem the contextual bandits problem with cross-learning. The best algorithms for the classical contextual bandits problem achieve $\tilde{O}(\sqrt{CKT})$ regret against all stationary policies, where $C$ is the number of contexts, $K$ the number of actions, and $T$ the number of rounds. We demonstrate algorithms for the contextual bandits problem with cross-learning that remove the dependence on $C$ and achieve regret $O(\sqrt{KT})$ (when contexts are stochastic with known distribution), $\tilde{O}(K^{1/3}T^{2/3})$ (when contexts are stochastic with unknown distribution), and $\tilde{O}(\sqrt{KT})$ (when contexts are adversarial but rewards are stochastic).