Breaking the Metric Voting Distortion Barrier

We consider the following well studied problem of metric distortion in social choice. Suppose we have an election with $n$ voters and $m$ candidates who lie in a shared metric space. We would like to design a voting rule that chooses a candidate whose average distance to the voters is small. However, instead of having direct access to the distances in the metric space, each voter gives us a ranked list of the candidates in order of distance. Can we design a rule that regardless of the election instance and underlying metric space, chooses a candidate whose cost differs from the true optimum by only a small factor (known as the distortion)? A long line of work culminated in finding deterministic voting rules with metric distortion $3$, which is the best possible for deterministic rules and many other classes of voting rules. However, without any restrictions, there is still a significant gap in our understanding: Even though the best lower bound is substantially lower at $2.112$, the best upper bound is still $3$, which is attained even by simple rules such as Random Dictatorship. Finding a rule that guarantees distortion $3 - \varepsilon$ for some constant $\varepsilon $ has been a major challenge in computational social choice. In this work, we give a rule that guarantees distortion less than $2.753$. To do so we study a handful of voting rules that are new to the problem. One is Maximal Lotteries, a rule based on the Nash equilibrium of a natural zero-sum game which dates back to the 60's. The others are novel rules that can be thought of as hybrids of Random Dictatorship and the Copeland rule. Though none of these rules can beat distortion $3$ alone, a careful randomization between Maximal Lotteries and any of the novel rules can.

Regret Minimization with Noisy Observations

In a typical optimization problem, the task is to pick one of a number of options with the lowest cost or the highest value. In practice, these cost/value quantities often come through processes such as measurement or machine learning, which are noisy, with quantifiable noise distributions. To take these noise distributions into account, one approach is to assume a prior for the values, use it to build a posterior, and then apply standard stochastic optimization to pick a solution. However, in many practical applications, such prior distributions may not be available. In this paper, we study such scenarios using a regret minimization model. In our model, the task is to pick the highest one out of $n$ values. The values are unknown and chosen by an adversary, but can be observed through noisy channels, where additive noises are stochastically drawn from known distributions. The goal is to minimize the regret of our selection, defined as the expected difference between the highest and the selected value on the worst-case choices of values. We show that the na\"ive algorithm of picking the highest observed value has regret arbitrarily worse than the optimum, even when $n = 2$ and the noises are unbiased in expectation. On the other hand, we propose an algorithm which gives a constant-approximation to the optimal regret for any $n$. Our algorithm is conceptually simple, computationally efficient, and requires only minimal knowledge of the noise distributions.

Fair for All: Best-effort Fairness Guarantees for Classification

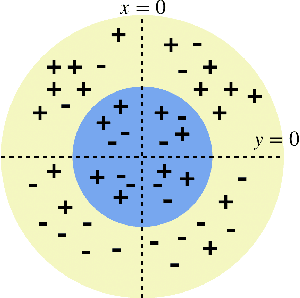
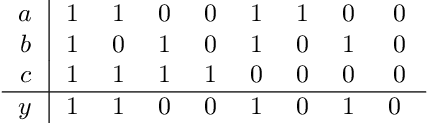
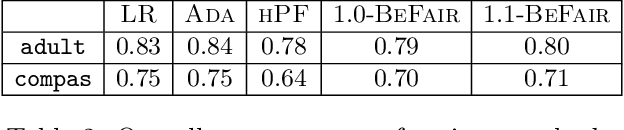
Standard approaches to group-based notions of fairness, such as \emph{parity} and \emph{equalized odds}, try to equalize absolute measures of performance across known groups (based on race, gender, etc.). Consequently, a group that is inherently harder to classify may hold back the performance on other groups; and no guarantees can be provided for unforeseen groups. Instead, we propose a fairness notion whose guarantee, on each group $g$ in a class $\mathcal{G}$, is relative to the performance of the best classifier on $g$. We apply this notion to broad classes of groups, in particular, where (a) $\mathcal{G}$ consists of all possible groups (subsets) in the data, and (b) $\mathcal{G}$ is more streamlined. For the first setting, which is akin to groups being completely unknown, we devise the {\sc PF} (Proportional Fairness) classifier, which guarantees, on any possible group $g$, an accuracy that is proportional to that of the optimal classifier for $g$, scaled by the relative size of $g$ in the data set. Due to including all possible groups, some of which could be too complex to be relevant, the worst-case theoretical guarantees here have to be proportionally weaker for smaller subsets. For the second setting, we devise the {\sc BeFair} (Best-effort Fair) framework which seeks an accuracy, on every $g \in \mathcal{G}$, which approximates that of the optimal classifier on $g$, independent of the size of $g$. Aiming for such a guarantee results in a non-convex problem, and we design novel techniques to get around this difficulty when $\mathcal{G}$ is the set of linear hypotheses. We test our algorithms on real-world data sets, and present interesting comparative insights on their performance.